代码随想录——二叉树-12.平衡二叉树

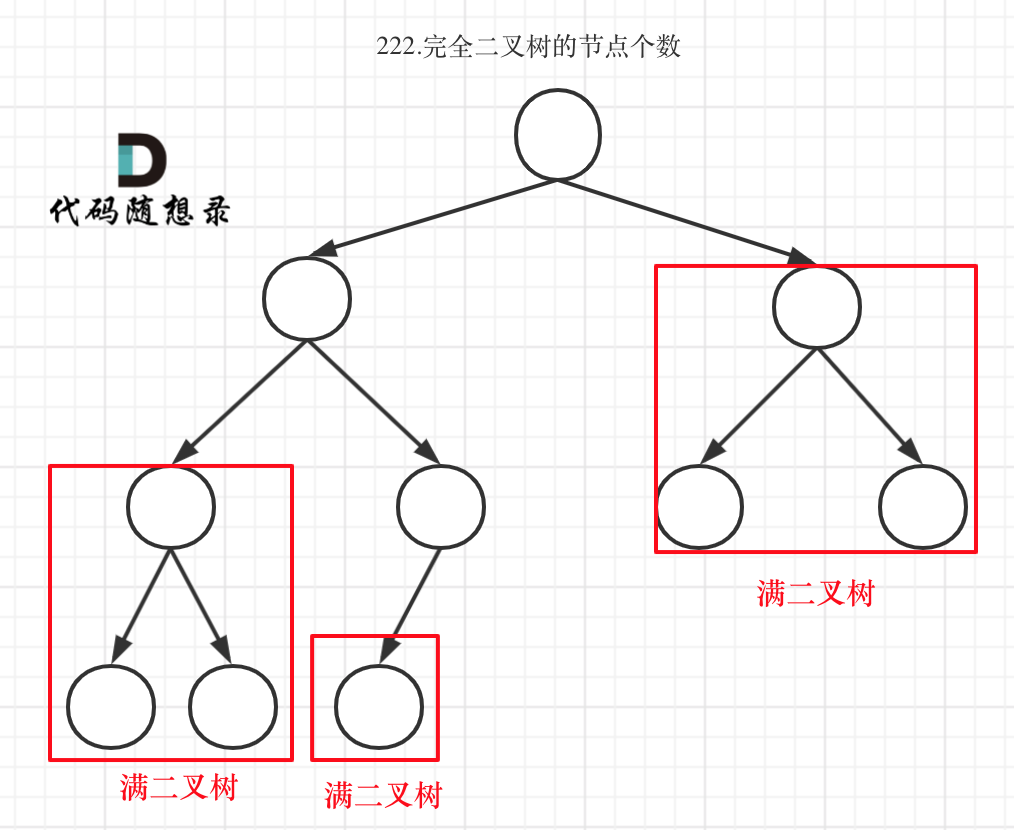
自顶向下递归（前序遍历）

这种方法是一开始想到的，虽然ac了但是对于它的本质却不清不楚，不知道时间复杂度，不知道属于前序遍历。

思路

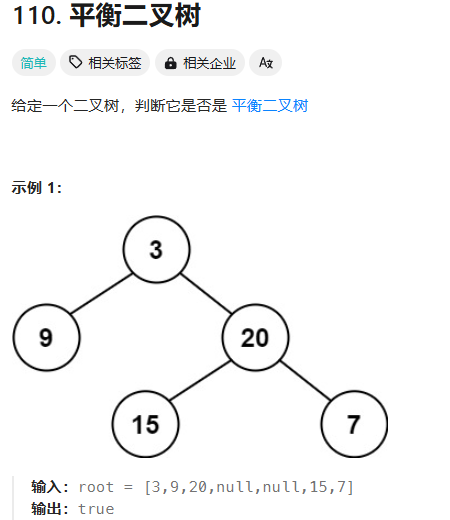
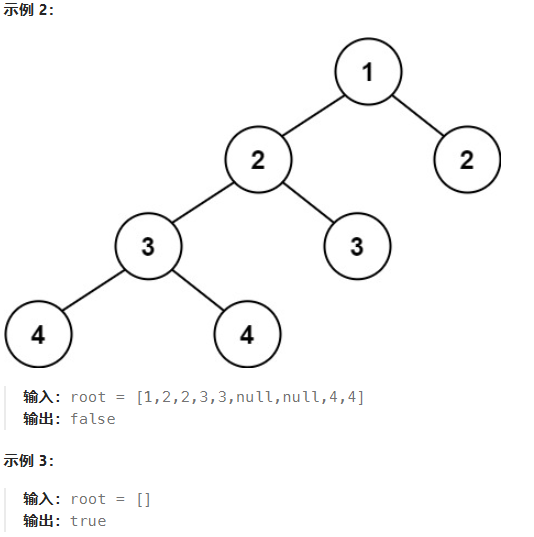
首先得到root节点的左右子树的深度（左右），若深度差绝对值大于1（中），则root为根的树不是平衡二叉树；
否则继续递归root的左右子树，其左右子树都是平衡二叉树时，root才是平衡二叉树。

代码

class Solution {
public:int depth(TreeNode* root){if(root == nullptr)return 0;return max(depth(root->left),depth(root->right)) + 1;}bool isBalanced(TreeNode* root) {if(root == nullptr)return true;int cha = depth(root->left) - depth(root->right);if(cha > 1 || cha < -1)return false;return isBalanced(root->left) && isBalanced(root->right);}};

复杂度

时间复杂度：O(n^2)，n是节点个数

最坏情况，二叉树是满二叉树，需要遍历所有节点，时间复杂度O(n)
对于节点p，如果它的高度是d，则height(p)会被调用d次（即遍历到它的每一个祖先节点时）。而最坏情况下，二叉树是链式结构，高度为n，此时总时间复杂度为O(n^2)

自底向上递归（后序遍历）

思路

代码

class Solution {
public:int height(TreeNode* root){if(root == nullptr)return 0;int lheight = height(root->left);int rheight = height(root->right);   //左右子树不是平衡二叉树就返回-1if(lheight == -1 || rheight == -1)return -1;//以root为根的树不是平衡二叉树也返回-1if(abs(lheight - rheight) > 1) return -1;//以root为根的树是平衡二叉树，则返回以root为根的树的深度return max(lheight,rheight) + 1;}bool isBalanced(TreeNode* root) {return height(root) >= 0;}};

复杂度