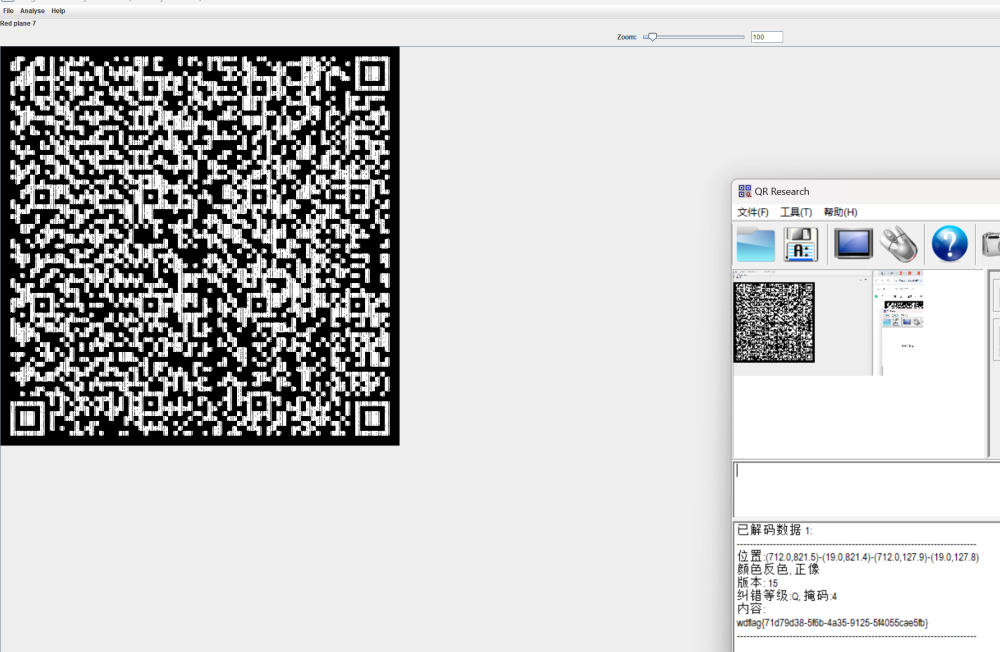
给定一个 R×CR×C 的方格矩阵。
矩阵左上角方格坐标为 (0,0)(0,0),右下角方格坐标为 (R−1,C−1)(R−1,C−1)。
每个方格中要么有南瓜,要么有干草。
南瓜分为大、中、小三种。
初始时,一个农民位于方格 (A,B)(A,B)。
他可以朝上下左右四个方向自由移动,但是他不能走出矩阵,也不能走进有干草的方格。
他每走进一个方格就可以将方格内的南瓜收走。
每个小南瓜价值 11 元,每个中南瓜价值 55 元,每个大南瓜价值 1010 元。
请你计算,他可以收获的全部南瓜的总价值。
保证农名的初始位置有南瓜。
输入格式
第一行包含整数 RR。
第二行包含整数 CC。
接下来 RR 行,每行 CC 个字符,表示方格矩阵的具体分布。其中,大南瓜用 L 表示,中南瓜用 M 表示,小南瓜用 S 表示,干草用 *。
再一行包含整数 AA。
最后一行包含整数 BB。
输出格式
一个整数,表示可以收获的全部南瓜的总价值。
数据范围
1≤R×C≤1051≤R×C≤105,
0≤A<R0≤A<R,
0≤B<C0≤B<C
输入样例1:
6
6
**LMLS
S*LMMS
S*SMSM
******
LLM*MS
SSL*SS
5
1输出样例1:
37样例1解释
矩阵的具体分布图如下所示,农民的可活动范围为黄色区域。
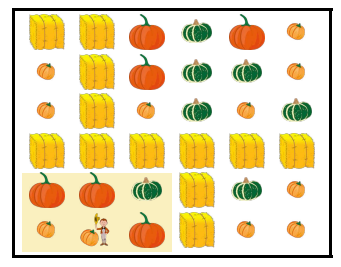
农民一共可以收获 22 个小南瓜,11 个中南瓜,33 个大南瓜,总价值为 2×1+1×5+3×10=372×1+1×5+3×10=37。
输入样例2:
6
6
**LMLS
S*LMMS
S*SMSM
***SLL
LLM*MS
SSL*SS
2
4输出样例2:
88样例2解释
矩阵的具体分布图如下所示,农民的可活动范围为黄色区域。
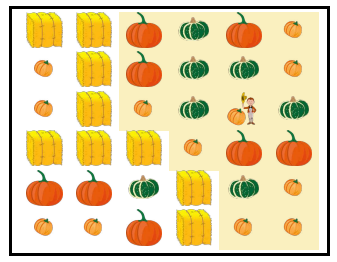
农民一共可以收获 88 个小南瓜,66 个中南瓜,55 个大南瓜,总价值为 8×1+6×5+5×10=888×1+6×5+5×10=88。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>using namespace std;int n, m;
vector<string> g;
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};int get_score(char c)
{if (c == 'S') return 1;if (c == 'M') return 5;return 10;
}int dfs(int x, int y)
{int res = get_score(g[x][y]);g[x][y] = '*';for (int i = 0; i < 4; i ++ ){int a = x + dx[i], b = y + dy[i];if (a < 0 || a >= n || b < 0 || b >= m || g[a][b] == '*') continue;res += dfs(a, b);}return res;
}int main()
{cin >> n >> m;g.resize(n);//表示将vector的大小调整为nfor (int i = 0; i < n; i ++ ) cin >> g[i];int x, y;cin >> x >> y;cout << dfs(x, y) << endl;return 0;
}