洛谷题单指南-二叉堆与树状数组-P3368 【模板】树状数组 2

原题链接：https://www.luogu.com.cn/problem/P3368

题意解读：树状数组应用-区间修改，单点求值

解题思路：

设原数组为s[N]，其差分数组为a[N]

操作一：区间修改

要对s[x] ~ s[y]每个数增加k，相当于对a[x]加k，对a[y + 1]减k，O(n)的操作变成了O(1)的操作,

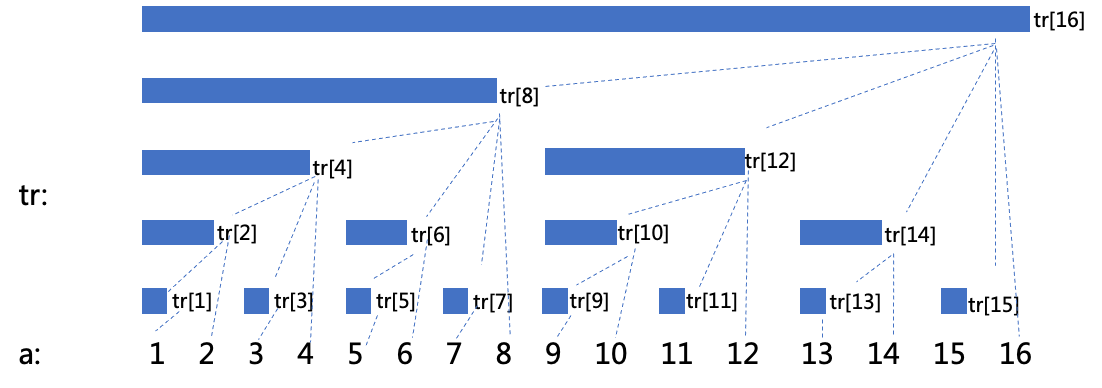
利用树状数组tr[N]的add(x, k), add(y + 1, -k)来实现对于a[N]的操作即可.

操作二：单点求值

要求s[x]的值，相当于求a[1] ~ a[x]所有数的和，

利用树状数组的sum(x)求和即可。

树状数组初始化：

初始化时，要对原数组的值求差分，添加到树状数组。

100分代码：

#include <bits/stdc++.h>
using namespace std;const int N = 500005;
int n, m;
int s[N], tr[N];int lowbit(int x)
{return x & -x;
}void add(int x, int val)
{for(int i = x; i <= n; i += lowbit(i)) tr[i] += val;
}int sum(int x)
{int res = 0;for(int i = x; i != 0; i -= lowbit(i)) res += tr[i];return res;
}int main()
{cin >> n >> m;for(int i = 1; i <= n; i++){cin >> s[i];add(i, s[i] - s[i - 1]); //构造差分的树状数组}int op, x, y, k;while(m--){cin >> op;if(op == 1){cin >> x >> y >> k;add(x, k);add(y + 1, -k);}else if(op == 2){cin >> x;cout << sum(x) << endl;}}return 0;
}