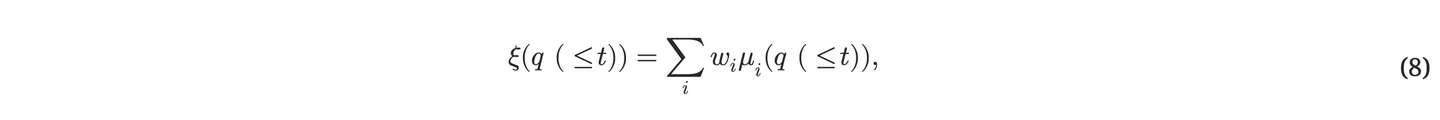T1 选取字符串
warning❗:本题解 前缀 含量过高。
挺典的 kmp。考虑到题目中的串都是一个串的前缀,那么所选出来的串,他们的前缀一定是最短的那个串。不妨直接枚举每一个前缀,也就是枚举每一个串,看他们是否可以作为前缀出现,hash即可,复杂度 \(\mathcal{O}(N^2)\)。换个思路,考虑有多少个串包含某一个前缀,预处理 kmp 的 next 数组可以 \(\mathcal{O}(N)\) 求出每个串的最大公共前后缀,不过前缀的前缀也是自己的前缀,所以需要做一个前缀和来统计每个前缀被多少个串包含。然后枚举前缀,令 \(tot\) 表示当前前缀的前后缀数量(包含自己),\(num\) 表示包含此前缀的串的数量,贡献就是:\((2tot+1)\times \binom{num}{k}\)。至于为什么是 \(2tot+1\),因为当前枚举的这个前缀可以和其它的前缀匹配,因为 \(p,q\) 分别为两种方案,所以乘2,加一是因为 \(p,q\) 可相同。
#include<bits/stdc++.h>
using namespace std;
constexpr int N = 1e6 + 5, M = 998244353;
int nxt[N], fac[N], inv[N], tot[N], num[N];
struct node{ int bg, nxt; }nd[N];
inline int qpow(int a, int k){int res = 1; while(k){if(k & 1) res = (long long)res * a % M;a = (long long)a * a % M; k >>= 1;} return res;
}
inline int add(initializer_list<int> Add){int res = 0;for(int v : Add) res = res + v >= M ? res + v - M : res + v;return res;
}
inline int mul(initializer_list<int> Mul){int res = 1;for(int v : Mul) res = (long long)res * v % M;return res;
}
inline int C(int a, int b){ return b > a ? 0 : mul({fac[a], inv[b], inv[a-b]}); }
int main(){freopen("string.in", "r", stdin); freopen("string.out", "w", stdout);ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int k; string str; cin>>k>>str; int n = str.size();fac[0] = inv[0] = 1;for(int i=1; i<=n+1; ++i) fac[i] = mul({fac[i-1], i});inv[n+1] = qpow(fac[n+1], M-2); for(int i=n; i>=1; --i) inv[i] = mul({inv[i+1], i+1});for(int i=1, j=0; i<n; ++i, j=nxt[i]){tot[i] = tot[nxt[i]] + 1;while(j && str[i] != str[j]) j = nxt[j];nxt[i+1] = j + (str[i] == str[j]);} tot[n] = tot[nxt[n]] + 1;for(int i=1; i<=n; ++i) num[i] = 1;for(int i=n; i>=1; --i) num[nxt[i]] += num[i];int ans = C(n+1, k);for(int i=n; i>=1; --i) ans = add({ans, mul({tot[i]*2+1, C(num[i], k)})});return cout<<ans, 0;
}
T2 取石子
问题模型:取石子(NIM)游戏,要求每个人每次取的石子数不能超过上一个人刚刚取的,第一个人最
开始可以取不超过 \(K\) 个。
考虑策略:
- 如果 \(\sum_i a_i\) 是奇数,先手取 \(1\) 个必胜,因为每个人之后都只能取 \(1\) 个;
- 否则,先手最优一定取偶数个并且后面每个人能取偶数个都只会取偶数个(否则留给对手总和为奇
数的情况,自己必败),所以可以递归到 \(K\gets \lfloor \frac{K}{2} \rfloor , a_i\gets \lfloor\frac{a_i}{2} \rfloor\)。
解得先手必胜当且仅当对于某个 \(t\le \log_2 K\),\(\sum{i=1}^n \lfloor \frac{a_i}{2^t}\rfloor\)模 \(2\) 和
为 \(1\),也即 \(\mathop{\oplus}i a_i \not\equiv 0\pmod {2^{\lfloor \log_2 K\rfloor}}\)。
定义 \(\mathrm{lowbit}(x)\) 表示整除 \(x\) 的最大的 \(2\) 的幂。先手第一步能必胜的策略必定是取
\((2k+1)\cdot \mathrm{lowbit}(\mathop{\oplus}i a_i)\)个。枚举取的堆,假设是第 \(i\) 堆,考虑枚举取
完之后另一个人面对的剩下的异或和的 \(\mathrm{lowbit}\),假设是\(2^t\),那么先手取的个数为 \(a_i - (\mathop{\oplus}{j\ne i} a_j)\oplus 2^t \pmod {2^{t+1}}\)。由于必胜,后手不能取到 \(2^t\),于是自己
这次取的个数也必须小于 \(2^t\)。枚举 \(t\) 依次判断即可。注意处理 \(t=\infty\)(取完之后异或和归零)
的情况。
综上,答案至多 \(O(n\log a)\) 种。
时间复杂度:\(O(n\log a)\)
说点儿人话:考场上手膜样例快睡着了,于是果断放弃。不过想来这个结论还是挺妙的。对于构造,假如除了当前 \(a_i\) 的异或和为 \(sum\),那么我要构造一种取法使得 \(sum\oplus (a_i-x)\) 的前 \(k\) 位一定没有 \(1\)。不妨直接枚举,如果这一位上 \(sum\) 是 \(0\),\(a_i\) 是 \(1\),那么肯定要把它减去(加到答案里),如果是 \(1\) 和 \(0\),就要考虑借位,不过鉴于从小到大枚举,直接减掉即可,后面一定会考虑得到。
#include<bits/stdc++.h>
using namespace std;
constexpr int N = 1e6 + 5;
#define lb(x) ((x) & (-x))
int a[N];
int main(){freopen("nim.in", "r", stdin); freopen("nim.out", "w", stdout);ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int n, k; cin>>n>>k; int sum = 0;for(int i=1; i<=n; ++i) cin>>a[i], sum ^= a[i];if(lb(sum) > k) return cout<<"0", 0;cout<<"1\n";for(int i=1; i<=n; ++i){int nw = a[i], tmp = sum ^ a[i];for(int j=0; j<=30; ++j) if((1 & (tmp >> j)) ^ (1 & (nw >> j))){nw -= 1 << j;if(nw < 0 || a[i] - nw > k) break;cout<<i<<' '<<(a[i] - nw)<<'\n';}} return 0;
}
T3 均衡区间
考虑到并不是所有的数都是有贡献的,那么考虑维护所有有贡献的数。拿 \(\min\) 来说,令 \(r\) 为当前右端点,并把 \(a_r\) 加到单调栈中,那么该单调栈的图像大致为这样:

那么单调栈中的每一个数都对应着一段贡献区间,即在这段区间里所有的点作为左端点到 \(r\) 的区间 \(\min\)都由那个数贡献。最小值不能由左右端点贡献,可以发现,只有红色的部分是合法的。可以以同样的方式处理出维护 \(\max\) 的单调栈,求这两个合法区间交的长度即可。使用线段树复杂度 \(\mathcal{O}(N\log N)\)。
代码有点小bug,应该是从严格大于、小于的点开始维护区间。
#include<bits/stdc++.h>
using namespace std;
constexpr int B = 1 << 13;
char buf[B], *p1 = buf, *p2 = buf, obuf[B], *O = obuf;
#define gt() (p1==p2 && (p2=(p1=buf)+fread(buf, 1, B, stdin), p1==p2) ? EOF : *p1++)
template <typename T> inline void rd(T &x){x = 0; int f = 0; char ch = gt();for(; !isdigit(ch); ch = gt()) f ^= x == '-';for(; isdigit(ch); ch = gt()) x = (x<<1) + (x<<3) + (ch^48);x = f ? -x : x;
}
template <typename T, typename ...TT> inline void rd(T &x, TT &...y){ rd(x), rd(y...); }
#define pt(ch) (O-obuf==B && (fwrite(obuf, 1, B, stdout), O=obuf), *O++ = (ch))
template <typename T> inline void wt(T x){if(x < 0) pt('-'), x = -x;if(x > 9) wt(x / 10); pt(x % 10 ^ 48);
}
#define fw fwrite(obuf, 1, O - obuf, stdout)
constexpr int N = 1e6 + 5;
int n, id, a[N];
namespace ST{#define ls (id << 1)#define rs (id << 1 | 1)struct node{ int l, r, num[3], tag; }t[N<<2];inline void pushup(int id){t[id].num[0] = t[ls].num[0] + t[rs].num[0];t[id].num[1] = t[ls].num[1] + t[rs].num[1];t[id].num[2] = t[ls].num[2] + t[rs].num[2];}inline void build(int id, int l, int r){t[id].l = l, t[id].r = r; t[id].tag = 0;t[id].num[0] = t[id].num[1] = t[id].num[2] = 0;if(l == r) return t[id].num[0] = 1, void();int mid = (l + r) >> 1;build(ls, l, mid), build(rs, mid+1, r);pushup(id);}inline void addtag(int id, int val){if(val == 1){t[id].num[2] += t[id].num[1]; t[id].num[1] = 0;t[id].num[1] += t[id].num[0]; t[id].num[0] = 0;} else if(val == -1){t[id].num[0] += t[id].num[1]; t[id].num[1] = 0;t[id].num[1] += t[id].num[2]; t[id].num[2] = 0;} else if(val == 2){t[id].num[2] += t[id].num[0]; t[id].num[0] = 0;} else {t[id].num[0] += t[id].num[2]; t[id].num[2] = 0;}t[id].tag += val;}inline void pushdown(int id){if(t[id].tag != 0){addtag(ls, t[id].tag);addtag(rs, t[id].tag);t[id].tag = 0;}}inline void modify(int id, int l, int r, int val){if(l > r) return;if(l <= t[id].l && t[id].r <= r) return addtag(id, val);pushdown(id); int mid = (t[id].l + t[id].r) >> 1;if(l <= mid) modify(ls, l, r, val);if(r > mid) modify(rs, l, r, val);pushup(id);}
}
namespace Sub2{int flag[N], Lans[N];struct XiaoLe{int st[N], tl; bitset<N> ok;inline void insert_mn(int x){while(tl && a[st[tl]] > a[x]){if(ok[st[tl]]){ST::modify(1, st[tl-1]+1, st[tl]-1, -1);ok[st[tl]] = 0;}--tl;} st[++tl] = x;if(tl > 1 && !ok[st[tl-1]]){ok[st[tl-1]] = 1;ST::modify(1, st[tl-2]+1, st[tl-1]-1, 1);}}inline void insert_mx(int x){while(tl && a[st[tl]] < a[x]){if(ok[st[tl]]){ST::modify(1, st[tl-1]+1, st[tl]-1, -1);ok[st[tl]] = 0;}--tl;} st[++tl] = x;if(tl > 1 && !ok[st[tl-1]]){ok[st[tl-1]] = 1;ST::modify(1, st[tl-2]+1, st[tl-1]-1, 1);}}}rmn, rmx;struct XiaoLe2{int st[N], tl; bitset<N> ok;inline void insert_mn(int x){while(tl && a[st[tl]] > a[x]){if(ok[st[tl]]){ST::modify(1, st[tl]+1, st[tl-1]-1, -1);ok[st[tl]] = 0;}--tl;} st[++tl] = x;if(tl > 1 && !ok[st[tl-1]]){ok[st[tl-1]] = 1;ST::modify(1, st[tl-1]+1, st[tl-2]-1, 1);}}inline void insert_mx(int x){while(tl && a[st[tl]] < a[x]){if(ok[st[tl]]){ST::modify(1, st[tl]+1, st[tl-1]-1, -1);ok[st[tl]] = 0;}--tl;} st[++tl] = x;if(tl > 1 && !ok[st[tl-1]]){ok[st[tl-1]] = 1;ST::modify(1, st[tl-1]+1, st[tl-2]-1, 1);}}}lmn, lmx;inline void solve(){ST::build(1, 1, n);lmn.st[0] = n+1, lmx.st[0] = n+1;for(int i=n; i>=1; --i){lmn.insert_mn(i);lmx.insert_mx(i);Lans[i] = ST::t[1].num[2];}for(int i=1; i<=n; ++i) wt(Lans[i]), pt(' ');pt('\n'); ST::build(1, 1, n);for(int i=1; i<=n; ++i){rmn.insert_mn(i); rmx.insert_mx(i);wt(ST::t[1].num[2]), pt(' ');} fw, exit(0);}
}
int main(){freopen("interval.in", "r", stdin); freopen("interval.out", "w", stdout);rd(n, id); for(int i=1; i<=n; ++i) rd(a[i]);if(id == 2){for(int i=1; i<=n; ++i) pt('0'), pt(' ');pt('\n');for(int i=1; i<=n; ++i) pt('0'), pt(' ');fw, exit(0);}Sub2::solve();
}
T4 禁止套娃
设选择的外层子序列下标为集合 \(I\),内层为集合 \(J\subseteq I\)。为了方便表述,设占位下标 $0\in
I,J$。同样只计贪心匹配的情况,限制如下:
- \(I\) 中相邻两个数 \(i,i'\),\(a{i+1\sim i'-1}\) 中不存在 \(=a{i'}\) 的值。
- \(J\) 中相邻两个数 \(j,j'\),\(a{I\cap(j,j')}\) 中不存在 \(=a{j'}\) 的值。
考虑对 \(J\) dp。\(f_i\) 表示目前考虑到 \(i\) 且内外层末尾均选 \(i\) 的答案。如果要从 \(f_j\) 转移过来,那
么就要决定 \(a_{j+1\sim i-1}\) 这部分如何选外层,设选择了集合 \(K\),限制如下;
- \(K\) 中相邻两个数 \(k,k'\),\(a{k+1\sim k'-1}\) 中不存在 \(=a{k'}\) 的值。
- \(K\) 中最大值 \(k_r\),\(a_{k_r+1\sim i-1}\) 中不存在 \(=a_i\) 的值。
- \(K\) 中任意 \(k\),\(a_k\ne a_i\)。
一个简洁的处理方法是,对于每一个 \(i\),dp 出 \(>\) 每个 \(j\) 的只需满足 1、3 条件的本质不同子序列
个数 \(g{i,j}\),真正转移时 \(f_i\xleftarrow{+}(g{i,j}-g_{pre_i,j})\cdot f_j\) 即可。最后汇总答案可以弄一个
必选的占位下标 \(n+1\)。
\(g\) 是 2D/0D,\(f\) 是 1D/1D,时间复杂度 \(\mathrm{O}(n^2)\),期望得分 \(100\)。
#include<bits/stdc++.h>
using namespace std;
constexpr int N = 5005, M = 1e9 + 7;
int n, a[N], f[N], g[N][N], pre[N], lst[N], suf[N], h[N];
inline int add(initializer_list<int> Add){int res = 0;for(int v : Add) res = res + v >= M ? res + v - M : res + v;return res;
}
inline int mul(initializer_list<int> Mul){int res = 1;for(int v : Mul) res = (long long)res * v % M;return res;
}
int main(){freopen("nest.in", "r", stdin); freopen("nest.out", "w", stdout);ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);cin>>n; for(int i=1; i<=n; ++i) cin>>a[i], suf[i] = n + 1;for(int i=1; i<=n; ++i) suf[pre[i] = lst[a[i]]] = i, lst[a[i]] = i;for(int i=1, sum=1; i<=n+1; ++i, sum=1) for(int j=i-1; j>=0; --j){g[i][j] = sum; h[j] = a[i] == a[j] ? 0 : sum;sum = add({sum, M-h[suf[j]], h[j]});} f[0] = 1;for(int i=1; i<=n+1; ++i) for(int j=0; j<i; ++j)f[i] = add({f[i], mul({add({g[i][j], M-g[pre[i]][j]}), f[j]})});return cout<<f[n+1], 0;
}