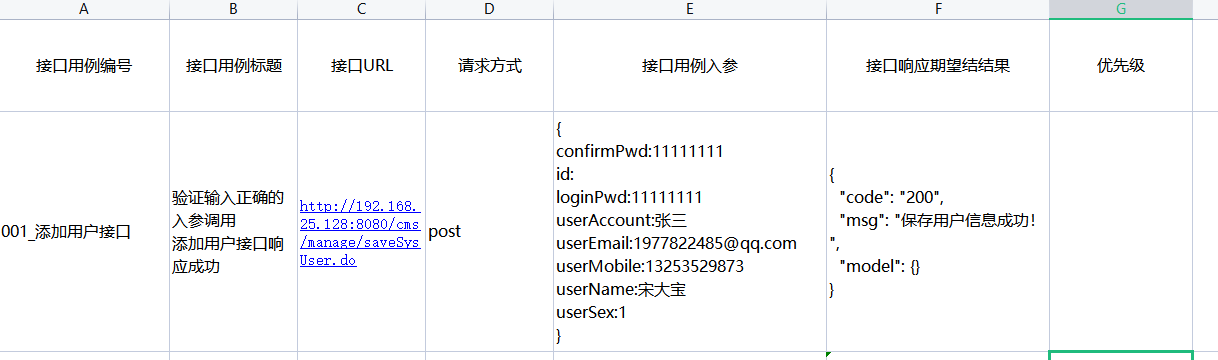
总结
完啦 A 不会做。肯定是神秘贪心题。不太好模拟啊。
算了猜个结论吧。\(m=1\) 是经典问题,把这个稍微引申一下。得到了一个 multiset 维护的做法。
然后猜对了。15min 切掉。很快码了一个对拍然后一直拍到比赛结束。
看 B。感觉不难。尝试设计 DP。
发现我啥也不会,所以先写个暴力找规律吧。
法克,暴力咋写。先跳吧。
C 一眼不可做啊。基本上没怎么想。看 D。
\(20\) 分不难。暴力排个序就好。\(n=2000\) 平方带 \(\log\) 能过吗?……时限 6s 那没事了。
想想性质 A。这不暴力,每次求个区间内的后继,然后最多只会跳 \(\log\) 次吗?主席树启动!
然后 \(60\) 到手。好水啊。
正解是不可能的。润了。回到 B。
稍微画了几个图模拟了一下,差不多在 10:50 左右的样子得到了一个很劣而且很没前途的解法。复杂度未知,大概能得 \(55\) 分。
写了很久,中间的关键部分重构了三四次。发现是 \(\mathcal O(n^5)\) 的。或许 \(40\) 分。
但是样例不过啊。调了很久(差不多在结束前 10min)过了样例。
结果跑得很快啊。最后一个大样例只跑了 6s。卡常启动!
然后时间太紧了只卡到 4.9s。不管了交吧。
\(100+60+0+20\)。T4:if (l1 == r1 && l2 == r2)。
总结
好的:
- T2 写完+调完了。虽然和正解 几乎没有关系。
不足:
- T4 若只错误。白丢 \(40\)。
- 基本没给 T3 的思考时间。
知识
T1:贪心,mutiset
T2:DP,组合
T4:复杂度分析,主席树
题解
A. 机械师 II
贪心。数据结构维护当前每个机械玩偶已经解决的 \(r\) 最大的事件。将事件按 \(r\) 排序,每次找到数据结构中 \(\le l_i\) 的最大的机械玩偶,让它做 \(i\)。找不到就跳过这个事件。
不难发现这个数据结构可以是 multiset。
B. 守墓人
首先求 \(f(u)\) 表示 \(u\) 的子树有多少种 dfs 方法。不难发现:
显然一个子树内的点在 dfs 序上是连续的。或者说,遍历到 \(u\) 后,接下来遍历的 \(sz_u\) 个点一定是 \(u\) 的子树。
画个小图。比如我们想求 \(v\) 的答案。
那么 dfs 序一定长这样:
其中两个蓝色括号里,一定会填上 \(1,3,4\) 这些子树。比如:
此时还有一段前缀和一段后缀未确定。因为这些点是 \(u\) 子树外的。
于是我们可以只对子树外的点的顺序计数。令 \(g(u,x)\) 表示 dfs 序第 \(x\) 个位置是 \(u\),这个前缀和后缀的方案数。显然答案为 \(g(u,x) \times f(u)\)。
如何转移?考虑 \(g(u) \to g(v)\) 的转移。
分别枚举 \(u\) 在 dfs 序中的位置和 \(v\) 在 dfs 序中的位置,不妨设为 \(i, j\),且 \(i < j\)。
根据上面说的,\([i+1,j-1]\) 这一段肯定要填上 \(\{1,3,4\}\) 的子集的子树。剩下的要填在后面。dfs 序中剩下的位置已经被 \(g(u,i)\) 考虑了,不用管它。
还是这张图。如果这样填:
那么转移条件是 \(sz_4+sz_1=j-i-1\)。然后 \(g(u,i) \times f(4) \times f(1) \times f(3) \to g(v, j)\)。
显然这一坨 \(f\) 的乘积可以最后一块考虑。我们只需要考虑 \(f(u,i) \to f(v,j)\)。也就是求有多少个 \(\{1,3,4\}\) 的子集的 \(sz\) 和为 \(j-i-1\)。
这是一个背包问题。对于一个 \(v\) 而言,计算这个答案的复杂度是立方级别的。也就是总复杂度 \(\mathcal O(n^4)\)。
注意到子树 \(2\) 的根对应的这个集合是全集(\(\{1,2,3,4\}\))去掉一个元素。于是考虑先对全局做一遍背包,然后每次退掉一个元素。也就是 [P4141消失之物](P4141 消失之物 - 洛谷 | 计算机科学教育新生态) 了。
提交记录 #719496 - 梦熊联盟
D. 先知
考虑这样操作:
- 找到 \([l1,r1]\) 中的最大值 \(x\)。
- 找到 \([l2,r2]\) 中最大的 \(<x\) 的值 \(y\)。
- 如果 \(y \ge \lfloor x / 2 \rfloor\) 则说明答案为 \(x+y\),直接退出。
- 否则,找到 \([l1,r1]\) 中最大的满足 \(\lfloor x' /2 \rfloor \le y\) 的 \(x'\)。如果 \(x' > y\) 则说明答案为 \(x+y\),直接退出。
- 否则,\(x \gets x'\),回到第二步。
正确性显然。
复杂度为啥正确?
如果第三步没有退出,一定有 \(y < \lfloor x / 2 \rfloor\)。如果第四步没有退出,一定 \(x' \le y\)。也就是说如果这一轮没有结束那么 \(x\) 一定减少一半。
所以复杂度是 \(\log\) 的。
找区间内一个数的前驱可以主席树。总复杂度 \(\mathcal O(n \log V \log n)\)。