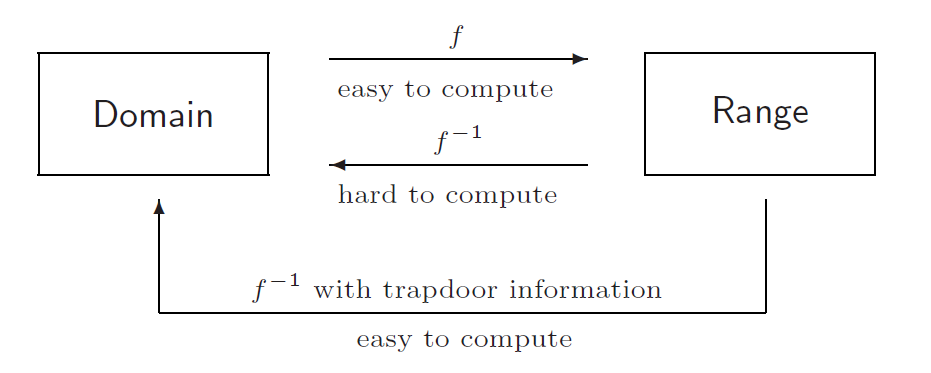
概念 1 单向函数和陷门信息
单向函数是一种可逆函数,其正向计算容易,但反向计算却非常困难。
安全的公钥加密系统(Public Key Cryptosystem, 简称PKC)基于具有陷门的单向函数。陷门是一种辅助信息,利用它可以轻松计算单向函数的反函数。
“陷门”一词来源于物理或机械陷阱的概念:单向性:就像一个带有单向机关的门,可以轻松通过,但无法轻易逆转回来。陷门信息:如果掌握了打开机关的关键(即陷门信息),逆转就会变得简单。
公钥(或非对称)密码系统的密钥由两个部分组成:私钥 $ k_{\text{priv}} $ 和公钥 $ k_{\text{pub}} \(。在实际中,\) k_{\text{pub}} $ 通常通过某种密钥生成算法从 $ k_{\text{priv}} $ 计算得出。对于每一对公钥/私钥 $ (k_{\text{priv}}, k_{\text{pub}}) $,都存在一个加密算法 $ e_{k_{\text{pub}}} $ 和一个相应的解密算法 $ d_{k_{\text{priv}}} $。加密算法 $ e_{k_{\text{pub}}} $ 是公开的,并且计算简单。同样,解密算法 $ d_{k_{\text{priv}}} $ 对于持有私钥 $ k_{\text{priv}} $ 的人来说计算简单,但对于仅知道公钥 $ k_{\text{pub}} $ 的人来说则非常困难。
人们认为私钥 $ k_{\text{priv}} $ 是函数 $ e_{k_{\text{pub}}} $ 的陷门信息,因为没有陷门信息时,计算 $ e_{k_{\text{pub}}} $ 的逆函数非常困难,但有了陷门信息后,这一计算就变得简单。此外,特别需要注意的是,从 $ k_{\text{priv}} $ 创建 $ k_{\text{pub}} $ 所使用的函数本身必须难以逆向计算,因为 $ k_{\text{pub}} $ 是公开信息,而 $ k_{\text{priv}} $ 允许高效解密。
概念 2 离散对数问题
设 $ p $ 为一个(较大的)素数。由于有限域的乘法群 \(\mathbb{F}_p^*\) 是循环群,取循环群的生成元 \(g\),这意味着 $ \mathbb{F}_p $ 中的每个非零元素都等于 $ g $ 的某个幂次。换句话说,以下元素列表:
是 $ \mathbb{F}_p^* $ 的所有元素的一种排列。
设 $ g $ 是 $ \mathbb{F}_p $ 的一个本原根,且 $ h $ 是 $ \mathbb{F}_p $ 的一个非零元素。离散对数问题(DLP)的定义是找到一个指数 $ x $,使得
我们称 $ x $ 为以 $ g $ 为底的$ h $ 的离散对数,记作 $ \log_g(h) $。
容易证明 \(\log_g(ab) = \log_g(a) + \log_g(b), \quad \forall a, b \in \mathbb{F}_p^*。\),而且由费马小定理可知因此, \(\log _g(h) \pm p-1\) 仍然满足式 \((1)\),所以 \(\log _g(h)\) 通常是在 \(\mathbb{Z}/(p-1)\mathbb{Z}\) 上定义的。离散对数 \(\log _g\) 是一个从乘法群 \(\mathbb{F}_p^*\) 到加法群 \(\mathbb{Z} /(p-1) \mathbb{Z}\) 的群同构。
Diffie–Hellman 密钥交换的思想和算法以及安全性分析
Diffie–Hellman 密钥交换算法解决了以下难题:
问题:
Alice 和 Bob 想要共享一个密钥来用于对称加密,但他们的通信渠道不安全。任何信息交换都会被窃听者 Eve 观察到。在这种情况下,Alice 和 Bob 如何共享一个密钥而不让 Eve 获取它?
解决方法:
Diffie 和 Hellman 利用有限域 $ \mathbb{F}_p^* $ 上离散对数问题的困难性提供了一种可能的解决方案。
算法步骤:
-
公开参数选择:
Alice 和 Bob 共同选择一个大的素数 $ p $ 和一个模 $ p $ 的非零整数 $ g $,并将 $ p $ 和 $ g $ 作为公开信息。例如,他们可以将这些值发布在各自的网站上。因此,Eve 也能获取这些值。为了更高的安全性,通常要求所选择的 $ g $ 的阶为有限域 $ \mathbb{F}_p^* $ 中的一个大素数。
-
私钥选择:
- Alice 随机选择一个私密整数 $ a $(称为 Alice 的私钥),并对任何人保密。
- Bob 随机选择一个私密整数 $ b $(称为 Bob 的私钥),也对任何人保密。
-
计算公钥:
- Alice 计算 $ A \equiv g^a \pmod{p} $ 并将 $ A $ 发送给 Bob。
- Bob 计算 $ B \equiv g^b \pmod{p} $ 并将 $ B $ 发送给 Alice。
Eve 通过监听通信渠道可以获得 $ A $ 和 $ B $ 的值。
-
计算共享密钥:
- Alice 使用 Bob 发送的 $ B $ 和自己的私钥 $ a $ 计算 $ K_A \equiv B^a \pmod{p} $。
- Bob 使用 Alice 发送的 $ A $ 和自己的私钥 $ b $ 计算 $ K_B \equiv A^b \pmod{p} $。
实际上,计算结果 $ K_A $ 和 $ K_B $ 是相同的,因为:
\[K_A \equiv B^a \equiv (g^b)^a \equiv g^{ba} \equiv g^{ab} \equiv (g^a)^b \equiv A^b \equiv K_B \pmod{p}. \] -
最终结果:
Alice 和 Bob 共享的密钥 $ K \equiv g^{ab} \pmod{p} $ 成为后续对称加密的密钥。
由于 Eve 仅能观察到 $ p \(、\) g \(、\) A $ 和 $ B $,但无法高效地计算 $ a $ 或 $ b $,因此她无法获得共享密钥 $ K $。
Diffie–Hellman 密钥交换算法总结:
| 步骤 | Alice 的操作 | Bob 的操作 | Eve 的可见信息 |
|---|---|---|---|
| 1 | 选择 $ a $,计算 $ A \equiv g^a \pmod{p} $ | 选择 $ b $,计算 $ B \equiv g^b \pmod{p} $ | $ p, g $ |
| 2 | 发送 $ A $ | 发送 $ B $ | $ A, B $ |
| 3 | 计算 $ K_A \equiv B^a \pmod{p} $ | 计算 $ K_B \equiv A^b \pmod{p} $ | 无法计算共享密钥 $ K $ |
最终,Alice 和 Bob 共享的密钥是 $ K\equiv K_A \equiv K_B \equiv g^{ab} \pmod{p} $。
注意,这种方法仅能实现密钥的秘密共享,而不是信息的秘密传输,因为在过程执行完毕之前 Alice 和 Bob 并不能事先确定所共享的具体密钥。
由于 Diffie–Hellman 密钥交换算法的安全性依赖于离散对数问题(DLP)的困难性,以下是对其安全性的详细分析:
Eve 的挑战(DHP 问题):
-
已知信息:
$ g, p, A = g^a \mod p, B = g^b \mod p $
Eve 需要计算 Alice 和 Bob 的共享密钥 $ g^{ab} \mod p $。 -
方法 1:解决 DLP
如果 Eve 能高效解决离散对数问题(DLP),她可以从 $ A = g^a \mod p $ 或 $ B = g^b \mod p $ 推导出 $ a $ 或 $ b $。接着,她可以轻松计算共享密钥 $ g^{ab} \mod p $。 -
问题所在:
实际上,Eve 不需要完整地解决 DLP 来计算共享密钥。她面临的问题被定义为 Diffie–Hellman 问题(DHP),这是一个可能更简单的计算任务。
Diffie–Hellman 问题(DHP)的定义:
问题描述:
设 $ p $ 为素数,$ g $ 为整数。已知 $ g^a \mod p $ 和 $ g^b \mod p $,计算 $ g^{ab} \mod p $。
DHP 与 DLP 的关系:
-
DHP 不难于 DLP:
如果 Eve 能高效解决 DLP,她可以推导出 $ a $ 和 $ b $,然后轻松计算 $ g^{ab} \mod p $。因此,DHP 的难度不超过 DLP。 -
DHP 是否等价于 DLP:
假设 Eve 有一个高效解决 DHP 的算法,问题是她是否可以利用该算法同样高效地解决 DLP。
当前结论: 尚不清楚。换句话说,目前没有证据表明 DHP 与 DLP 在计算复杂性上是等价的。
实际安全性:
-
当前的安全标准建议选择:
- $ p $ 为一个大约 1000 位的素数(即 $ p \approx 2^{1000} $)。
- $ g $ 为 $ \mathbb{F}_p^* $ 中一个阶为大素数(大约为 $ p/2 $)的元素。
-
这些选择使得:
- 暴力破解 DHP 或 DLP 的计算成本极高。
- 即使 Eve 使用现代计算能力,也无法在合理的时间内解决这些问题。
-
然而,DLP 和 DHP 之间的复杂性关系仍未完全确定,这是一项重要的研究课题,决定了 Diffie–Hellman 算法的长期安全性。
总结:Diffie–Hellman 算法的安全性主要依赖于 DHP 的计算难度,而 DHP 不难于 DLP。尽管解决 DHP 并不需要完整解决 DLP,但尚未明确两者是否是同等难度的计算问题。这是 Diffie–Hellman 算法安全性研究的一个核心问题。