LeetCode 367[有效的完全平方数]

题目

链接

LeetCode 367[有效的完全平方数]

详情

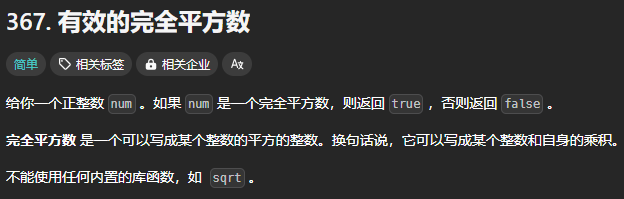
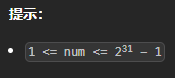
实例

提示

题解

思路

求算术平方根，逐渐遍历的话，数值小应该是没问题的，但是数值大的话时间应该会超出限制

本质是：给定一个数字，在范围内找一个数字的平方为该数，找到了则输出ture，找不到则输出false

转换一个思路，即给定一个数字，在范围内找出该数，也就是查找问题，最基本的方法就是二分查找

 

初始值设定最小值 iMin 为 0，最大值 iMax 为给定值 num

开始循环：

求取中间值 iMid = (iMin + iMax) / 2

取中间值的平方 iMul = iMid * iMid

若 iMul 等于 num，则可以找着算术平方根，即返回 true

若 iMul > num，即 iMid > sqrt(num)，即所求值小于 iMid，需要在 iMin 到 iMid -1 范围中查找，即 iMax = iMid - 1

若 iMul < num，即 iMid < sqrt(num)，即所求值大于 iMid，需要在 iMid + 1 到 iMax 范围中查找，即 iMin = iMid + 1

继续执行循环，直到 iMin > iMax，退出循环，此时为找不到算术平方根，故返回false

代码

class Solution {
public:bool isPerfectSquare(int num) {int iMin = 0;int iMax = num;while (true){long long iMid = (iMin + iMax) / 2;long long iMul = iMid * iMid;if (num == iMul)return true;if (num > iMul)iMin = iMid + 1;elseiMax = iMid - 1;if (iMin > iMax)return false;}}
};