题目传送门
题目大意：
给定一颗无根树，有一个节点是源点，度数为 \(1\) 的点是汇点，树上的边有最大流量。除源点和汇点外，其它点不储存水，即流入该点的水量之和等于从该点流出的水量之和。整个水系的流量定义为原点单位时间内能发出的水量。
现在需要求出：在流量不超过最大流量的前提下，选取哪个点作为源点，整个水系的流量最大，输出最大值。
思路：
朴素的想法是枚举某个点作为源点，然后做树形 dp，设 \(f_u\) 表示从点 \(u\) 往下流向子树的最大流量，不难得出状态转移方程：
\[f_u = \sum\limits_{j\in Son(u)}\begin{cases}\min(w_i, f_j) & \deg_j > 1\\w_i & \deg_j = 1\end{cases}
\]
对于每个点都这样做一遍，取 \(\max\)，时间复杂度 \(O(n^2)\)。
暴力 \(\texttt{Code:}\)
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 200010, M = 400010;
typedef long long ll;
int T, n;
int h[N], e[M], ne[M], w[M], idx;
int deg[N];
ll f[N];void init() {for(int i = 1; i <= n; i++)deg[i] = 0, h[i] = -1;
}inline void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}void dfs(int u, int fa) {f[u] = 0;for(int i = h[u]; ~i; i = ne[i]) {int j = e[i];if(j == fa) continue;dfs(j, u);if(deg[j] == 1) f[u] += w[i];f[u] += min(f[j], (ll)w[i]);}
}void solve() {scanf("%d", &n);init();for(int a, b, c, i = 1; i < n; i++) {scanf("%d%d%d", &a, &b, &c);add(a, b, c), add(b, a, c);deg[a]++, deg[b]++;}ll ans = 0;for(int i = 1; i <= n; i++) dfs(i, -1), ans = max(ans, f[i]);printf("%lld\n", ans);
}int main() {scanf("%d", &T);while(T--) {solve();}return 0;
}
因为这个题是一个无根树，而我们又要枚举根节点，所以不难想到用换根 dp 来代替源点的枚举。
所以考虑用换根 dp 来优化。
来回顾一下换根 dp 的基本思路：
- 第一次 dfs，任选一个点为根进行方才的树形 dp；
- 第二次 dfs，从相同的根出发，再扫描一遍从父节点向子结点更新信息，这里多半会用到剔除贡献的问题，要么记最大/次大值和具体从哪个点更新（这个主要用于最大/最小的不满足可减性的信息），要么从第一遍 dfs 的信息更新处倒推（这个一般用于满足可减性的信息）。
对应到这个题上就是思考子节点流向父节点的信息怎么计算。
先画个图：
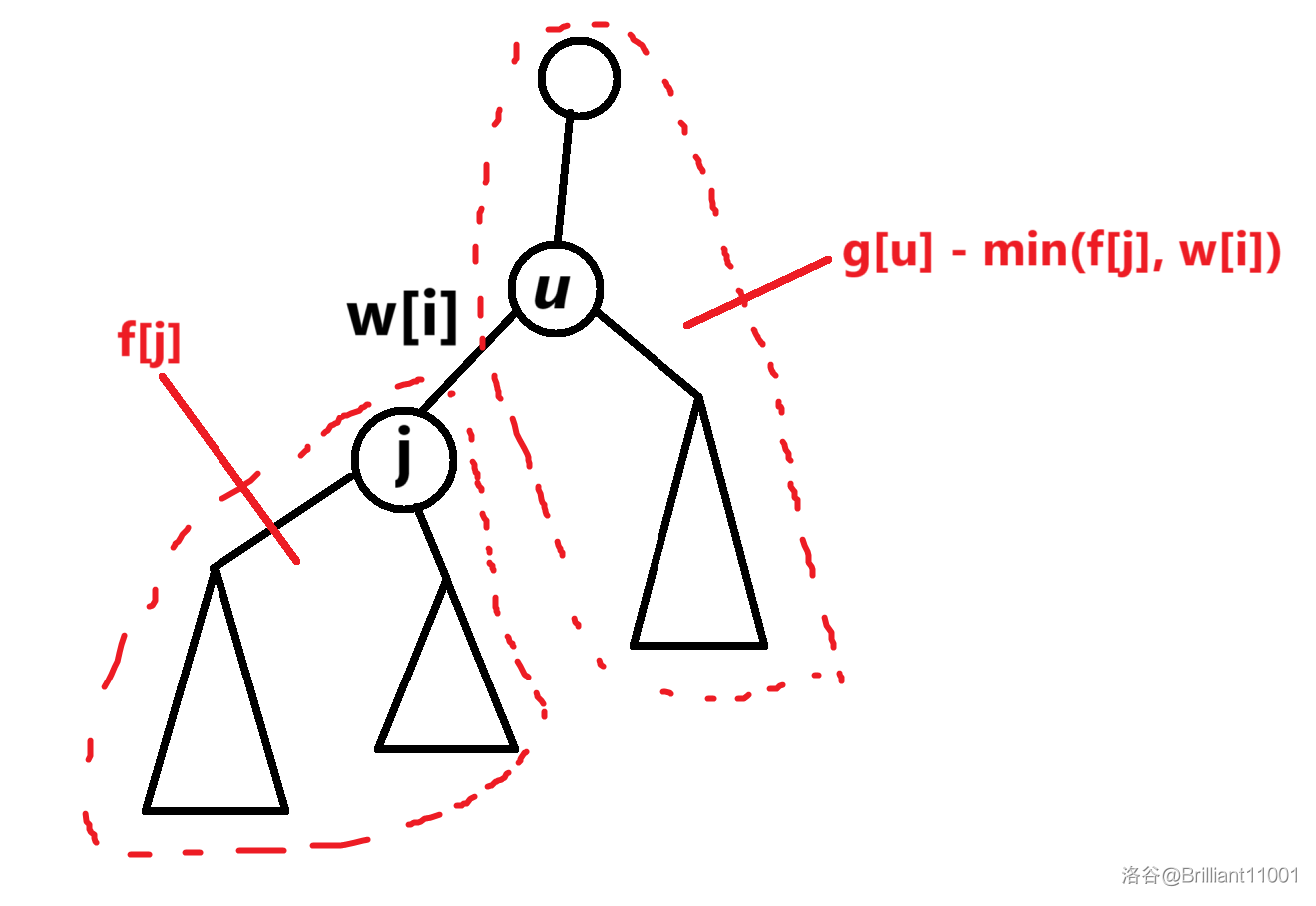
这里 \(g_u\) 表示 \(u\) 为源点的最大流量。
这道题的信息显然具有可减性。
如图，我们可以考虑先去掉 \(j\) 子树对 \(g_u\) 的贡献得到以 \(u\) 为源点的其他贡献，然后这一部分实际就是从 \(j\) 往上流的最大流量，直接和 \(f_j\) 相加就得到了 \(g_j\)。
但是这里有个魔鬼细节，需要考虑节点的度数，因为度数为 \(1\) 的点在第一遍 dfs 时是直接加上的 \(w_i\)，所以在去掉贡献的时候需要判一下。父节点也基本同理。
那么这道题就结束了，时间复杂度 \(O(n)\)。
\(\texttt{AC Code:}\)
#include <cstring>
#include <iostream>
#include <algorithm>using namespace std;const int N = 200010, M = 400010;
typedef long long ll;
int T, n;
int h[N], e[M], ne[M], w[M], idx;
int deg[N];
ll f[N], g[N];void init() {for(int i = 1; i <= n; i++)deg[i] = 0, h[i] = -1;
}inline void add(int a, int b, int c) {e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}void dfs(int u, int fa) {f[u] = 0;for(int i = h[u]; ~i; i = ne[i]) {int j = e[i];if(j == fa) continue;dfs(j, u);if(deg[j] == 1) f[u] += w[i];else f[u] += min(f[j], (ll)w[i]);}
}void dfs2(int u, int fa) {for(int i = h[u]; ~i; i = ne[i]) {int j = e[i];if(j == fa) continue;g[j] = f[j];if(deg[u] == 1) g[j] += w[i];else if(deg[j] == 1) g[j] += min((ll)w[i], g[u] - (ll)w[i]);else g[j] += min((ll)w[i], g[u] - min((ll)w[i], f[j]));dfs2(j, u);}
}void solve() {scanf("%d", &n);init();for(int a, b, c, i = 1; i < n; i++) {scanf("%d%d%d", &a, &b, &c);add(a, b, c), add(b, a, c);deg[a]++, deg[b]++;}dfs(1, -1);g[1] = f[1];dfs2(1, -1);ll ans = 0;for(int i = 1; i <= n; i++)ans = max(ans, g[i]);printf("%lld\n", ans);
}int main() {scanf("%d", &T);while(T--) {solve();}return 0;
}
