大模型--QLoRA、GPTQ：模型量化02--24

目录

• 1. 参考
• 2. 量化简介
• 3. QLoRA
  • NF4 数据类型
• 4. GPTQ
  • OBD：Optimal Brain Damage
  • OBS：Optimal Brain Surgeon
  • OBC
  • GPTQ 的创新点
• 5 各大开源模型量化实现
• 6 后续方向探讨

1. 参考

https://zhuanlan.zhihu.com/p/646210009?utm_psn=1845389883864133633

2. 量化简介

模型量化是将浮点数值转化为定点数值，同时尽可能减少计算精度损失的方法。

具体而言，模型量化是一种压缩网络参数的方式，它将神经网络的参数（weight）、特征图（activation）等原本用浮点表示的量值换用定点（整型）表示，在计算过程中，再将定点数据反量化回浮点数据，得到结果。

模型量化实现建立在深度网络对噪声具有一定的容忍性上，模型量化相当于对深度网络增加了一定的噪声（量化误差），如果量化位数合适，模型量化基本不会造成较大的精度损失。

为什么要做量化？
模型量化既能减少资源消耗，也能提高运行速度，使大规模推理服务的性能提升。

对哪些数值做量化？
可以对模型参数（weight）、激活值（activation）或者梯度（gradient）做量化。

通常而言，模型的参数分布较为稳定，因此对参数 weight 做量化较为容易。
然而，模型的激活值往往存在异常值，直接对其做量化，会降低有效的量化格点数，导致精度损失严重，因此，激活值的量化需要更复杂的处理方法（如 SmoothQuant）。

常见的量化精度有哪些？
通常可以将模型量化为 int4、int8 等整型数据格式。

量化方法有哪些分类？

• QAT（Quant-Aware Training） 也可以称为在线量化（On Quantization）。它需要利用额外的训练数据，在量化的同时结合反向传播对模型权重进行调整，意在确保量化模型的精度不掉点。
• PTQ （Post Training Quantization）也可以称为离线量化（Off Quantization）。它是在已训练的模型上，使用少量或不使用额外数据，对模型量化过程进行校准，可能伴有模型权重的缩放。

PTQ （Post Training Quantization）又可以分两种：

• 训练后动态量化（PostDynamic Quantization）不使用校准数据集，直接对每一层 layer 通过量化公式进行转换。QLoRA 就是采用这种方法。
• 训练后校正量化（Post Calibration Quantization）需要输入有代表性的数据集，根据模型每一层 layer 的输入输出调整量化权重。GPTQ 就是采用这种方法。

在线性量化下，浮点数与定点数之间的转换公式如下：

R 表示量化前的浮点数
Q 表示量化后的定点数
S（Scale）表示缩放因子的数值
Z（Zero）表示零点的数值

对称量化中，量化前后的 0 点是对齐的，因此不需要记录零点。它适合对分布良好且均值为 0 的参数进行量化。因此对称量化常用于对 weight 量化。

非对称量化（如右图所示）中，量化前后 0 点不对齐，需要额外记录一个 offset，也就是零点。非对称量化常用于对 activation 做量化。

稍后要介绍的 QLoRA 和 GPTQ 都是对 weight 做量化，因此均采用对称量化的方法。

模型量化具体是怎么实现的？
对称量化中，零点 Z = 0，一般不记录，我们只需要关心如何求解 Scale
由于 weight 几乎不存在异常值，因此我们可以直接取 Scale 为一个 layer 或 block 内所有参数的最大绝对值，
于是所有的参数都在 [-1, 1] 的区间内。

这里需要引入 Block-wise quantization 的概念。通常情况，为了避免异常值（outlier）的影响，我们会将输入 tensor 分割成一个个 block，每个 block 单独做量化，有单独的 scale 和 zero，因此能使量化的精度损失减少（见下图橙色的误差部分）。

这个图的下半部分没看懂

3. QLoRA

QLoRA 同时结合了模型量化 Quant 和 LoRA 参数微调两种方法
因此可以在单张48GB的 GPU 上对一个65B 的大模型做 finetune。
QLoRA 的量化方法（由 bitsandbytes 库提供 backend）也是 Transformers 官方的模型量化实现。

运用 QLoRA 的微调方法训练的模型 Guanaco 在多项任务上表现强劲，
Guanaco-65B 模型在 Open LLM Leaderboard 排名第二，大幅超越了原始的 llama-65B。
正因为 QLoRA 的高效训练方法和在下游任务的优秀表现，自公开 Guanaco 模型后，QLoRA 的这套方法也开始得到许多人的关注。

QLoRA 针对模型权重（weight）做量化，采用的是对称量化算法，量化过程基本同上面讲述的方法一致。我们主要来看它的量化创新点。

• 采用新的NF（NormalFloat） 数据类型，它是对于正态分布权重而言信息理论上最优的数据类型，同时，NF 类型有助于缓解异常值的影响；
• Double Quant，对于量化后的 scale 数据做进一步的量化；
  这两点很重要。。

NF4 数据类型

normal float 4
新的数据类型，可以看成新的格点分配策略。我们用一张图说明 int4 数据类型和 NF4 数据类型的区别。

解释：
int4 的格点分布是均匀的，然而模型的权重通常服从均值为 0 的正态分布，因此格点的分布和数据的分布不一致。这会导致格点“供需”的不匹配。
靠近 0 点的数据很多，但可用的格点数就相对较少，这样大量参数 round 的粒度较粗，会导致模型量化的精度受损；
远离 0 点的数据较少，而可用的格点数相对多，这部分的少量数据不需要太高的量化精度，因此部分格点就被浪费了。
NF4 的格点按照正态分布的分位数截取，格点分布两端稀疏，中间密集，格点分布与数据分布一致。这样格点分配的效率就大大增加了，同时精度受损也不会太大。

4. GPTQ

GPTQ 的思想最初来源于 Yann LeCun 在 1990 年提出的 OBD 算法，随后 OBS、OBC（OBQ） 等方法不断进行改进，而 GPTQ 是 OBQ 方法的加速版。GPTQ 的量化有严谨的数学理论推导，所有的算法步骤都有理论支撑。为了理解 GPTQ 的思想，我们需要先介绍 OBD -> OBS -> OBQ 的演进过程。

OBD：Optimal Brain Damage

OBD 实际上是一种剪枝方法，用于降低模型复杂度，提高泛化能力。
剪枝直接权重置为0
量化是float-->int-->float存在精度的损失

如果要在模型中去除一些参数（即剪枝），直觉上想，我们希望去除对目标函数 E 影响小的参数。

其中：
为参数的一阶偏导
为海森矩阵（参数的二阶偏导）的一个元素

OBD 做了一些假设，对上式进行简化：

• 不考虑高阶项
• 模型训练已充分收敛 一阶偏导均为 0
• 假设删除任意一个参数后，其他参数对目标函数的影响不变--（这个不成立呀）于是也可以不考虑海森矩阵中的交叉项：

进一步简化：

删除一个参数对目标函数的影响就是所以我们只要计算海森矩阵 就可以知道每个参数对目标的影响。
然后就可以按照影响从小到大给参数排个序，这样就确定了参数剪枝的次序。

OBS：Optimal Brain Surgeon

OBS 认为，参数之间的独立性不成立，我们还是要考虑交叉项，

用向量/矩阵形式表达会更加简明：

删除一个权重 也就是的第 q 维固定为。但其他维度的值可变，可以用于减少删除该权重带来的目标偏离。 -- 这句话很关键 这也是逐层量化的 思想来源

上面的约束条件，我们可以表示为一个等式：

是一个 one-hot 向量，第 q 个位置是 1 ，其余位置是 0。

思想：冻住某一行（剪枝就是全部置为0）其他的参数可以优化，减小由于剪枝或者量化带来的损失。
我们希望找到最合适的权重使得删除它对目标的影响最小。这可以表示为一个最优化问题：

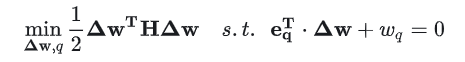
Lagrange 乘数法求解：

得到：

于是，我们也只需要求解海森矩阵的逆就可以计算每个参数对目标的影响。
然后就可以按照影响从小到大给参数排个序，这样就确定了参数剪枝的次序。同时，每次剪枝一个参数，其他的参数也按照更新一次。

这个公式就能告诉wq对于L的影响，从小到大排序，决定剪枝哪个，其他的参数根据更新。

这里的思想一直沿用到了 GPTQ 算法：
对某个block内的所有参数逐个量化，每个参数量化后，需要适当调整这个 block 内其他未量化的参数，以弥补量化造成的精度损失。

OBC

OBD 和 OBS 都存在一个缺点，就是剪枝需要计算全参数的海森矩阵（或者它的逆矩阵）。
在动辄上亿参数的神经网络下求解海森矩阵显然不可能。
于是，可以假设参数矩阵的同一行参数互相之间是相关的，而不同行之间的参数互不相关，这样，海森矩阵就只需要在每一行内单独计算就行啦。

为了求解海森矩阵，需要确定目标函数的具体形式。
令参数矩阵W的维度为OBC 论文的目标函数定义为：

一行一行的计算损失，总损失为每一行损失之和。

直观来看，就是参数量化前后，给同样的输入（具有代表性的校准数据），输出结果的差异要尽可能小。

由于每一行的参数独立，所以我们只需要对每一行的量化后参数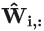求海森矩阵：

这个很关键呀！！！！

如果我们对一行共个参数删除 k 个参数，那么 OBC 的算法流程如下：

从 for 循环开始逐行分析：
Line 1：找到对目标函数影响最小的参数 p
Line 2：对参数 p 剪枝，并更新其他参数
Line 3：删除海森矩阵的 p 行 p 列，再求逆（这里用了数学的等价表达，降低了计算复杂度）

该算法的时间复杂度为

OBQ （和OBC是同一篇文章）指出，剪枝是一种特殊的量化（即剪枝的参数等价于量化到 0 点），我们只需要修改一下 OBC 的约束条件即可：

OBQ 对一行做量化的时间复杂度为 ，因此对整个参数矩阵做量化的时间复杂度为 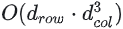。至此，GPTQ 的前置介绍就基本结束了。

GPTQ 的创新点

OBQ 的算法复杂度还是太高了，GPTQ 对 OBQ 做了一些算法和性能上的优化，因而可以实现大模型的高效量化。

• OBS 采用贪心策略，先量化对目标影响最小的参数；但 GPTQ 发现直接按顺序做参数量化，对精度影响也不大。
• Lazy Batch-Updates，延迟一部分参数的更新，它能够缓解 bandwidth 的压力；
• Cholesky Reformulation，用 Cholesky 分解求海森矩阵的逆，在增强数值稳定性的同时，不再需要对海森矩阵做更新计算，进一步减少了计算量。

其中第三点的优化（即不再需要对海森矩阵做更新计算）是靠 Cholesky 分解的数学特性去实现的，如果感兴趣，可以进一步研读 GPTQ 的论文和代码。

5 各大开源模型量化实现

MOSS：采用 GPTQ 量化算法，同时用自己的 calibration 数据集，权重包含：

• qweight，量化后权重，int32
• qzeros，量化后零点，int32
• scales，fp16
• g_idx，int32，推测应该是 group_index 的意思
  模型推理以 OpenAI Triton 作为 backend，主要做推理过程的反量化计算。

目前以 LLaMA 为基底的模型，多数都有开源社区的 GPTQ 量化实现，可能是 GPTQ 的影响力和知名度更大吧，但它未必是模型量化的最优选择，毕竟 GPTQ 仍然无法解决异常值问题和 Activation 量化。

6 后续方向探讨

1. Hopper 架构的 FP8 精度计算
   NVIDIA H100/H800 开始支持 FP8 的 kernel 运算。
   如果能训练出一个 FP8 预训练模型，那么我们无需量化就可以做 FP8 的推理服务。相比于 FP16，FP8 能带来 2 倍的 FLOP/s 提升，所需显存大大降低，同时通讯量也能有所降低。相比于 int8 量化，FP8 推理不需要量化/反量化的计算过程。

考虑到 H100 SXM 的带宽为 3TB/s，在计算强度最优，也就是计算时间和通讯时间均衡的情况下，单机推理的 batch size 至少可以增大到 256 或 512，这能有效地将 LLM 扩展到许多用户。

同时，原有的 FP16 模型也可以量化到 FP8。并且（在小模型场景下）FP8 量化模型的精度要显著优于 int8。
因此，基于 FP8 的训练和推理流程值得进一步研究。

2. Activation quant 的理论和应用
   对激活值做量化，可以大幅减少训练/推理过程的显存需求（以及在模型并行等情况下，显著减少通讯量）。SmoothQuant 就是一种比较有效的对 weight 和 activation 量化的方法。
   尽管对 Activation 量化要困难许多，现有的研究也正在探索 weight + activation 量化的最优方法，以此提升大模型训练与推理的整体速度，降低推理延迟，同时大幅度降低显存。