【论文精读】
Lora:Low-rank adaptation of large language models
论文地址:Lora:Low-rank adaptation of large language models
年份:2021
引用量:8000+
关键词:LLM的高效微调
- 【论文精读】
- Lora:Low-rank adaptation of large language models
- 1. 背景
- 2. Lora方法
- 3. 实验
- 3.1 实验设置
- 3.2 与其他的微调方法进行对比:
- 3.3 在四个模型上进行了实验
- 3.4 消融实验
- 4. 待更新:为什么\(\Delta W\)是低秩的?
1. 背景
现在,LLM训练的主要方法是:首先在通用任务上进行大规模的预训练,然后对预训练好的模型进行微调,以便更好的适应下游任务。
那么如何对模型进行微调呢?
一个简单的想法是:使用特定的任务,对模型的全部参数进行微调。这种方法叫做全量微调。
但是,LLM的参数量非常大,以GPT3为例,GPT3拥有大约175B个参数,如果对GPT3进行全量微调的话,这个成本太高了,令人无法接受。
因此,就提出了各种各样的方法来优化微调过程,这些优化方法统称为高效微调。
本文提出的Lora就是高效微调方法的一种,也是近年来最知名的一种。
2. Lora方法
Lora的基本思想是什么呢?
假设预训练后,模型的参数矩阵是$W_0\in\mathbb{R}^{d\times d} \(,在微调过程中,梯度是\)\Delta W \in\mathbb{R}^{d\times d} \(,那么在微调后,模型的参数矩阵变为\)W_0+\Delta W$。
作者认为,实际上,\(\Delta W\)的秩是很低的,因此,可以把\(\Delta W\)分解成两个低维的矩阵,即 \(\Delta W = BA\),其中\(B\in \mathbb{R}^{d\times r},A\in \mathbb{R}^{r\times d}\),且\(r\ll d\)。
那么,微调时只需要分别更新\(B,A\)两个矩阵,最后再计算二者的乘积\(BA\),就可以得到梯度\(\Delta W\)。
这样一来,直接更新\(\Delta W\)时,需要更新的参数有\(d^2\)个;但是将\(\Delta W\)分解为\(B,A\)的乘积后,只需要更新$d\times r + r \times d = 2rd \(个参数。由于\)r\ll d$,因此\(2rd\ll d^2\),大大减少了参数量。
还是以GPT3-175B为例,当\(d=12288\)时,令\(r\)等于1或者2,就能达到很好的微调效果。
若模型的输入为\(x\),前向传播后,模型的输出为\(h = W_0x\),那么在梯度更新之后,模型的输出为
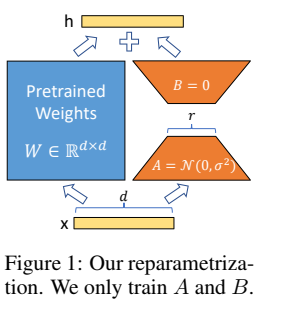
在微调开始时,将\(A\)初始化为随机高斯分布,将\(B\)初始化为零矩阵。此外,我们在梯度\(BA\)前乘一个缩放因子\(\frac{\alpha}{r}\),其中\(\alpha\)是常数,\(r\)是\(B\)和\(A\)的维度。这种缩放机制的好处是,当我们需要改变\(r\)的值时,不必频繁地调整其他超参数。
并且,对于Transformer结构的LLM,在使用Lora进行微调时,作者冻结了其中MLP层的参数,仅仅对Attention层的参数进行了微调。
可以用一张图来表示Lora的计算过程
3. 实验
结论:实验结果表明,使用LoRA方法进行微调,比起其他微调方法,不仅参数量更少,而且在多数任务上得分更高。
3.1 实验设置
- 为了简单起见,在绝大多数实验中,作者使用Lora对Attention层中的\(W_q\),\(W_v\)进行微调,其他的参数保持冻结状态。
3.2 与其他的微调方法进行对比:
-
全量微调(\(FT\))
在微调过程中,所有模型参数都进行梯度更新。一种简单的变体是仅更新某些层而冻结其他层,例如可以仅仅调整最后两层\(FT^{top2}\)。
-
\(BitFit\):仅仅调整偏置(bias),冻结其他所有参数。
-
前缀Embedding微调\(PreEmbed\):在输入文本前添加一串特殊标记作为"前缀"。这些标记不具有实际含义,而是充当可训练的参数。微调时,只需要对前缀进行训练。推理时,我们将训练好的前缀添加到新的输入中,模型就能输出满足特定任务需求的结果。
-
前缀层微调\(PreLayer\):前缀层微调不仅为输入添加前缀,还直接为每个Transformer层添加单独的前缀。具体来说,在普通的前缀微调中,前缀仅在输入时起作用;而在前缀层微调中,当数据流经模型的每一层时,都会遇到专门为该层设计的前缀参数。在推理时,新的输入会依次通过这些带有专属前缀的层,从而得到更精准的任务输出。
-
适配器微调:最早的设计(\(Adapter^H\))是在每个注意力模块和MLP模块后添加适配器层。后来的研究者提出了多种改进版本:\(Adapter^L\)和\(Adapter^P\)仅在MLP模块后添加适配器,而\(Adapter^D\)则通过选择性地删除一些适配器层来进一步提升效率。
3.3 在四个模型上进行了实验
-
\(\mathrm{RoBERTa}_{base},\mathrm{RoBERTa}_{large}\)
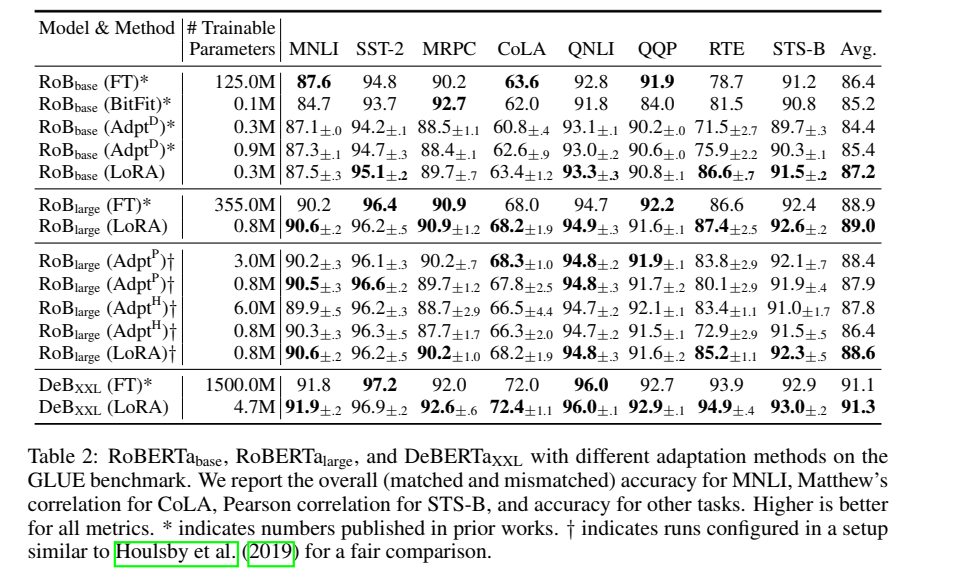
\(\mathrm{RoBERTa}\)是\(\mathrm{BERT}\)的升级版。作者从 HuggingFace Transformers 库中获取预训练好的 \(\mathrm{RoBERTa}_{base}\)(1.25 亿参数)和 \(\mathrm{RoBERTa}_{large}\)(3.55 亿参数),并比较不同高效微调方法在 GLUE 基准任务上的性能。为了确保公平比较,在与适配器比较时,作者对 LoRA 的评估方式进行了两个关键更改。首先,对所有任务使用相同的批量大小,并使用长度为 128 的序列以匹配适配器baseline。其次,对于 MRPC、RTE 和 STS - B 任务,我们将模型初始化为预训练模型,而不是像全量微调baseline那样初始化为已经适应 MNLI 任务的模型。
-
\(\mathrm{DeBERTa}\)
\(\mathrm{DeBERTa}\)也是 BERT 的一个变体。作者主要比较了在GLUE上,LoRA 是否与完全微调的\(\mathrm{DeBERTa}\ XXL\)(15 亿参数)的性能相匹配。
-
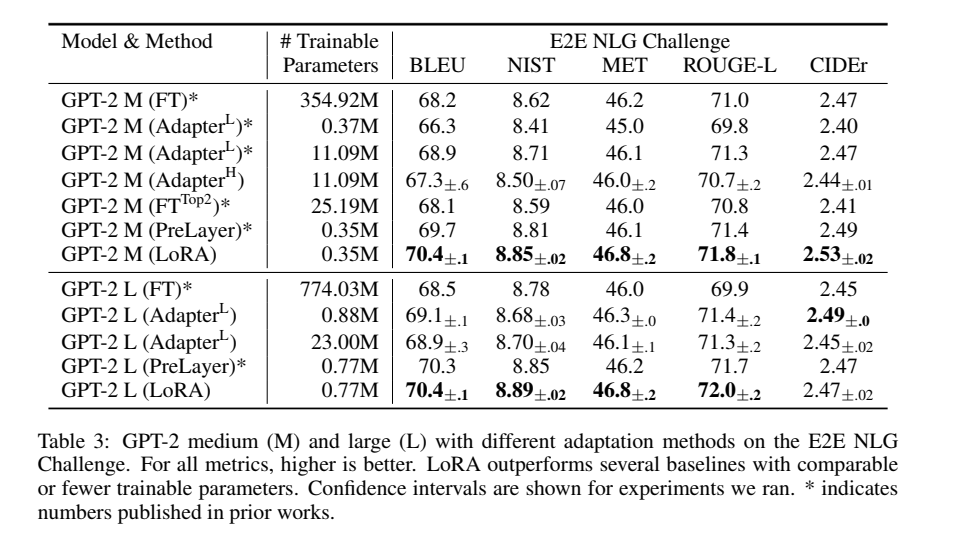
\(\mathrm{GPT-2}_{medium},\mathrm{GPT-2}_{large}\)
在表明 LoRA 可以成为自然语言理解(NLU)中全量微调的替代方案之后,作者希望回答: LoRA 在自然语言生成(NLG)模型(如 GPT - 2 中型和大型)上是否仍然占优。由于空间限制,表 3 仅展示在端到端自然语言生成挑战(E2E NLG Challenge)上的结果。
-
\(\mathrm{GPT-3} \ \ 175B\)
如表 4 所示,对于\(\mathrm{GPT-3} \ \ 175B\),LoRA 在三个数据集上都达到或超过了全量微调baseline。
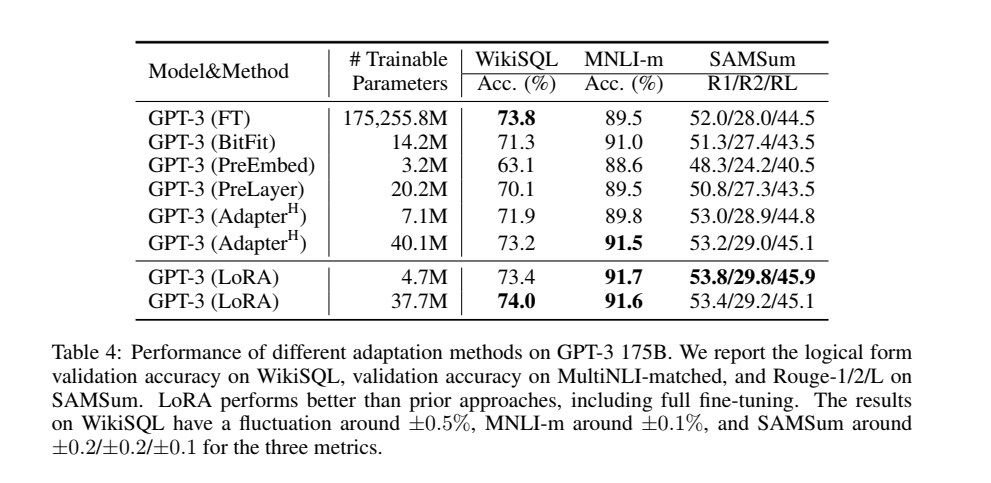
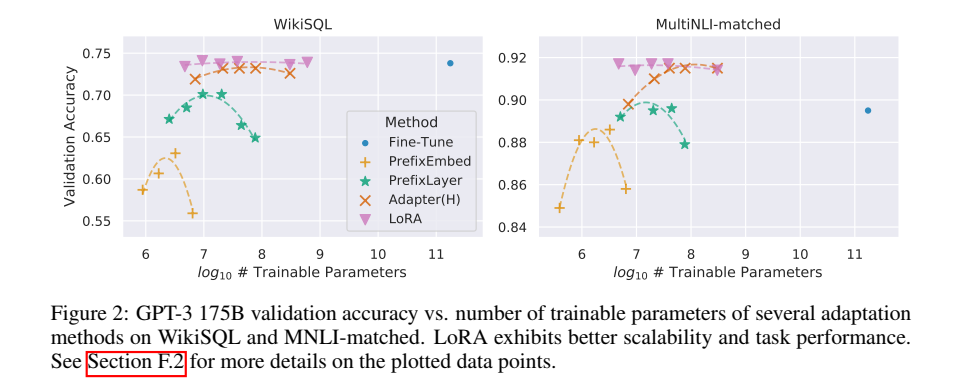
请注意,并非所有方法都能从更多的可训练参数中单调受益,如图 2 所示。作者观察到,当使用超过 256 个特殊标记进行前缀嵌入调优或超过 32 个特殊标记进行前缀层调优时,性能会显著下降。作为对比,当可训练参数增加时,Lora表现出了更强的可扩展性。
3.4 消融实验
作者在\(\mathrm{GPT-3}\)上进行了消融实验,实验表明:
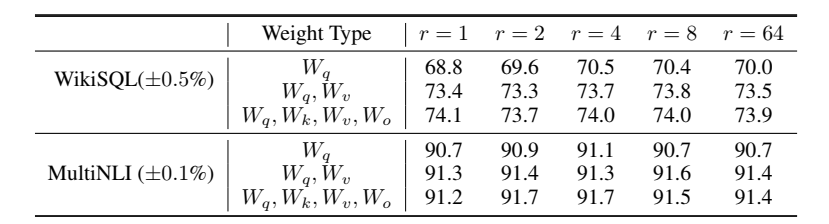
- 在固定训练参数量的前提下,不断调整训练的矩阵以及\(r\)的大小,最终发现,同时训练Attention层中的所有权重矩阵得分最高。
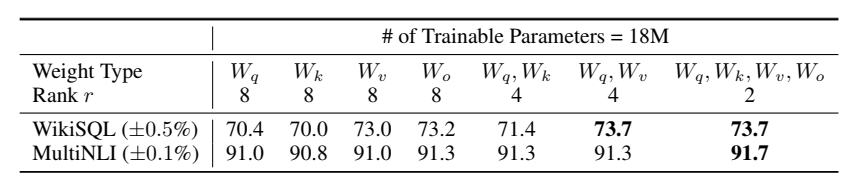
- 不固定训练参数量,直接调整\(r\)的大小,发现\(r=2,4\)时得分较高。