【评价指标】ROC曲线与AUC

一、前置知识

​ 真阳性(TPR)：正样本被正确分类个数与所有正样本的总数的比值

\[TPR = \frac{TP}{TP+FN} \]

​ 假阳性(FPR)：负样本被错误分类个数与所有负样本的总数的比值

\[FPR=\frac{FN}{FN+TN} \]

​ 其中，TP表示正确分类的正样本，TN表示正确分类的负样本，FN表示错误分类的负样本，FN表示错误分类的负样本

二、ROC基本内容

[!tip]

在机器学习与深度学习模型中，模型输出阈值\(\tau\)的设置会直接影响到结果的判断

​ 在二分类中一般采用Sigmoid激活函数输出结果。如图所示，x轴表示最后模型的输出概率，y轴表示经过sigmoid的变换后的输出结果，对应的TPR、FPR如表示所示，可以发现不同阈值的结果不同。

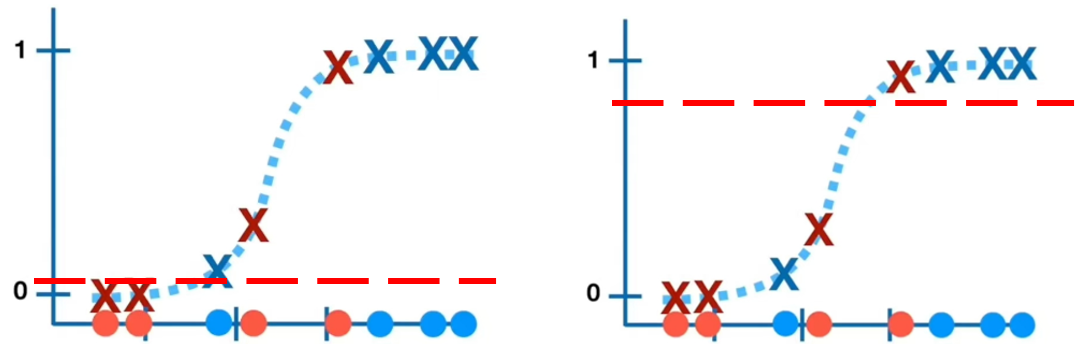
	TPR	FPR
左图	0.5	1
右图	0.75	0.75

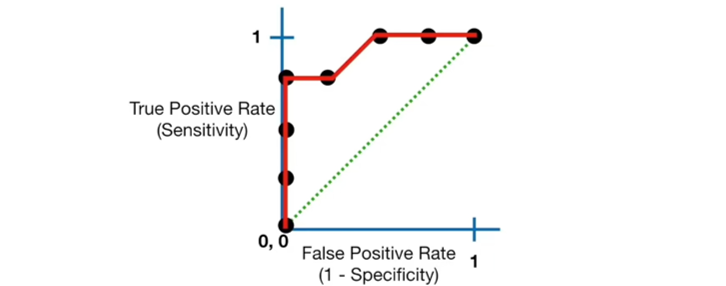
​ 不同阈值的设置会造成大量的参数和结果，为此，ROC曲线以FPR为x轴，TPR为y轴绘制二维图像，在ROC图上的特殊线：

• y = 1：表示正样本全部判断正确，并且x值越小模型的效果越好；
• x = 0：表示负样本全部没有误判，并且y值越大模型的效果越好；
• y = x：表示TPR = FPR，（1，1）点表示正样本全部判断正确，负样本全部错判；

三、代码实现

def calculate_roc_acc(y, y_prop):y = np.array(y)y_prop = np.array(y_prop)sorted_indexs = np.argsort(-y_prop) # 默认从小到大将索引排序，所以从大到小需要负号y = y[sorted_indexs]y_prop = y_prop[sorted_indexs]posNum = sum(y)negNum = len(y) - posNum# 记录不同阈值下的TPR和FPRTPRS = [0]FPRS = [0]# 阈值初始化thresholds = y_prop[np.argsort(-y_prop)]for threshold in thresholds:TP = np.sum((y_prop >= threshold) & (y == 1))  # 预测为正且实际为正FP = np.sum((y_prop >= threshold) & (y == 0))  # 预测为正但实际为负TPRS.append(TP / posNum)FPRS.append(FP / negNum)AUC = 0for i in range(1, len(FPRS)):AUC += (FPRS[i] - FPRS[i - 1]) * (TPRS[i] + TPRS[i - 1]) / 2return FPRS, TPRS, AUC

四、可视化代码

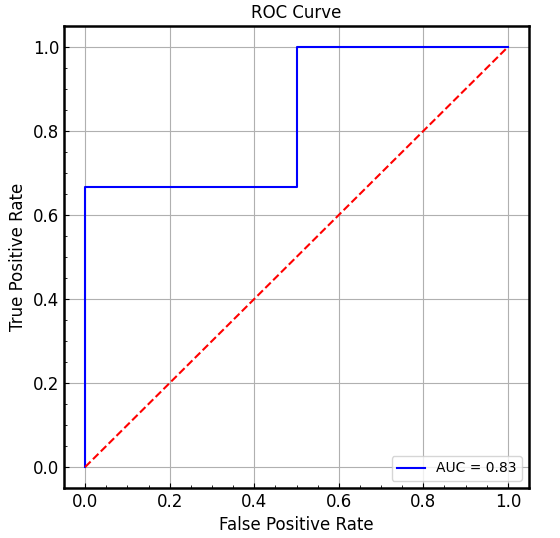
def plot_roc_curve(FPR, TPR, auc):plt.rcParams["axes.linewidth"] = 1.8plt.rcParams["axes.labelsize"] = 12plt.rcParams["xtick.minor.visible"] = Trueplt.rcParams["ytick.minor.visible"] = Trueplt.rcParams["xtick.direction"] = "in"plt.rcParams["ytick.direction"] = "in"plt.rcParams["xtick.labelsize"] = 12plt.rcParams["ytick.labelsize"] = 12plt.rcParams["xtick.top"] = Falseplt.rcParams["ytick.right"] = False# plt.rcParams['font.sans-serif'] = ['SimHei']plt.figure(figsize=(6, 6))plt.plot(FPR, TPR, label=f"AUC = {auc:.2f}", color='blue')plt.plot([0, 1], [0, 1], 'r--')plt.title("ROC Curve")plt.xlabel("False Positive Rate")plt.ylabel("True Positive Rate")plt.legend(loc="lower right")plt.grid()plt.show()