前言

        之前我们已经介绍过一种非顺序数据结构，是散列表。

JavaScript散列表及其扩展http://t.csdn.cn/RliQf        还有另外一种非顺序数据结构---树。

树数据结构

        树是一种分层数据的抽象模型。公司组织架构图就是常见的树的例子。

        

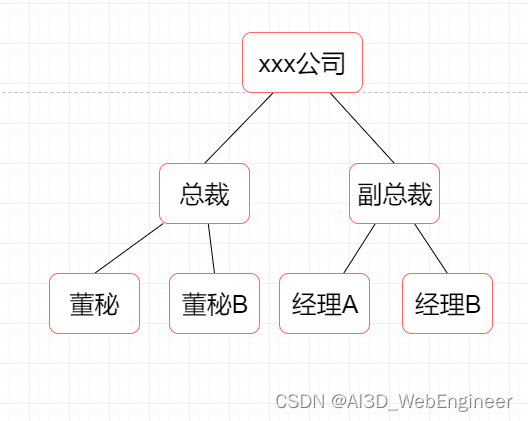
相关术语

        一个树结构，包含若干父子关系的节点。每个节点（除了根节点）都有一个父子点以及0个或多个子节点。

        树中的每个元素都叫做节点。

        位于树的顶部的节点叫做根节点。

        节点分为外部节点和内部节点。外部节点没有子节点。内部节点有子节点。

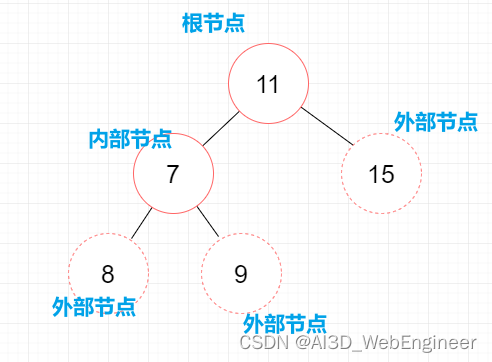
        一个节点（除了根节点）可以有祖先和后代。

        祖先节点包括 父节点、祖父节点、曾祖父节点等。

        后代节点包括子节点、孙子节点、曾孙节点等。

         

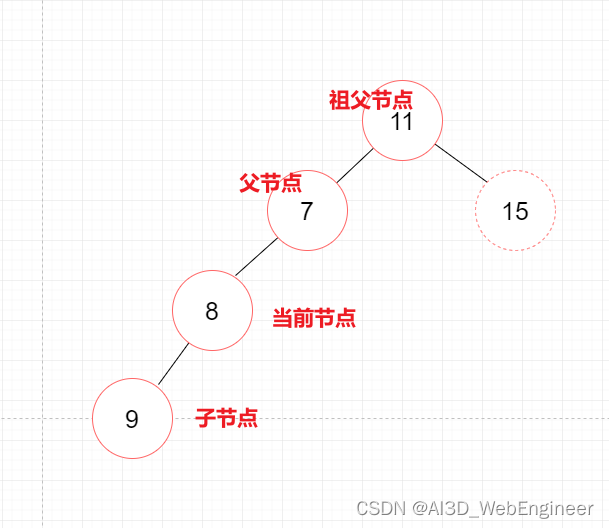
        子树：由节点和它的后代组成 

         节点的一个属性是深度。节点的深度取决于它的祖先节点的数量。

        树的高度属性取决于所有节点深度的最大值。

二叉树

         二叉树的节点最多只能有两个子节点。 

        

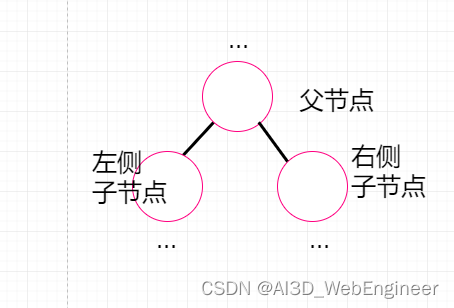
         二叉树的设计是为了让我们写出更高效地在树中插入、查找和删除节点的算法。

        二叉搜索树

        二叉树中的一种，只允许你在左侧节点存储（比父节点）小的值。在右侧节点存储（比父节点）大的值。

创建BinarySearchTree类（二叉搜索树）

        我们需要先设计节点类。

        通过示意图我们可以发现二叉树的节点跟链表的子节点很像。链表的节点包含值和前后引用。而树的节点包含了值和左右两侧节点的引用。

        在树相关的术语中，我们也把树的节点称之为键。

        键类：

export class Node {constructor(key) {this.key = key;this.left = undefined;this.right = undefined;}toString() {return `${this.key}`;}
}

        二叉查询树类：

export default class BinarySearchTree {constructor() {// 根节点this.root = undefined;}
}

        向二叉查询树中插入一个键：

import { defaultCompare } from '../util';
export default class BinarySearchTree {constructor(compareFn = defaultCompare) {this.compareFn = compareFn;this.root = undefined;}
}

 这里需要导入自定义的对比方法（为了对比插入节点值和想要比较的节点的节点值），这里展示一个常用的比较方法。当然你完全也可以自定义自己的比较方法。

const Compare = {LESS_THAN: -1,BIGGER_THAN: 1,EQUALS: 0
};
export function defaultCompare(a, b) {if (a === b) {return Compare.EQUALS;}return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}

insert(value) {if (this.root == null) {this.root = new Node(value)}else {this.insertNode(this.root, value)   }
}

insertNode(node, key) {if (this.compareFn(key, node.key) === Compare.EQUALS)  {// 重复节点不生成return false ;}else if (this.compareFn(key, node.key) === Compare.LESS_THAN) {if (node.left == null) {node.left = new Node(key);} else {this.insertNode(node.left, key);}} else if (node.right == null) {node.right = new Node(key);} else {this.insertNode(node.right, key);}
}

 测试：

const bbb = new BinarySearchTree();
bbb.insert(11)
bbb.insert(22)
bbb.insert(9)
bbb.insert(15)

得到：

完整代码：

class Node {constructor(key) {this.key = key;this.left = undefined;this.right = undefined;}toString() {return `${this.key}`;}
}
const Compare = {LESS_THAN: -1,BIGGER_THAN: 1,EQUALS: 0
};
function defaultCompare(a, b) {if (a === b) {return Compare.EQUALS;}return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}
class BinarySearchTree {constructor(compareFn = defaultCompare) {this.compareFn = compareFn;this.root = undefined;}insert(value) {if (this.root == null) {this.root = new Node(value)}else {this.insertNode(this.root, value)  }}insertNode(node, key) {if (this.compareFn(key, node.key) === Compare.EQUALS)  {// 重复节点不生成return false ;}else if (this.compareFn(key, node.key) === Compare.LESS_THAN) {if (node.left == null) {node.left = new Node(key);} else {this.insertNode(node.left, key);}} else if (node.right == null) {node.right = new Node(key);} else {this.insertNode(node.right, key);}}
}

树的遍历

三种方法：中序、先序、后序

中序遍历

中序遍历是一种以上行顺序访问树节点的遍历方式。

中序遍历不是从中间开始遍历，至于为什么叫中序遍历，请看后文。

应用于：对树进行排序操作。

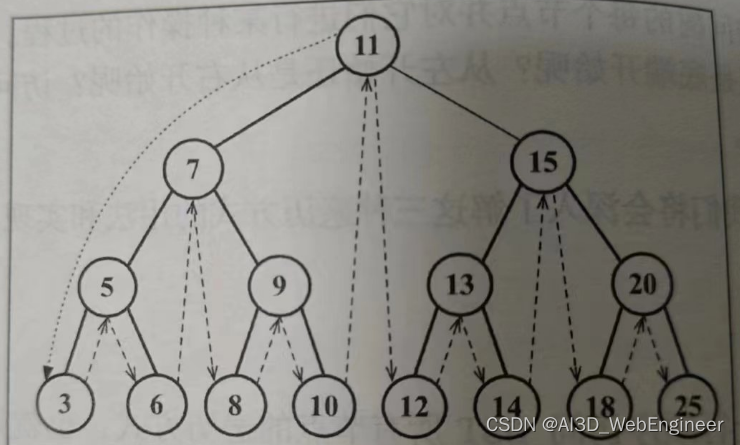
  inOrderTraverseNode(node, callback) {if (node != null) {this.inOrderTraverseNode(node.left, callback);callback(node.key);this.inOrderTraverseNode(node.right, callback);}}

这里的逻辑用了递归的思想。从上至下遍历到最左边最下面的节点然后再自下往上开始回调。

写个实例试试：

 添加遍历方法：

class BinarySearchTree {...inOrderTraverse(callback) {this.inOrderTraverseNode(this.root, callback);}inOrderTraverseNode(node, callback) {if (node != null) {this.inOrderTraverseNode(node.left, callback);callback(node.key);this.inOrderTraverseNode(node.right, callback);}}...
}

var aa = new BinarySearchTree()
aa.insert(11)
aa.insert(7)
aa.insert(15)
aa.insert(5)
aa.insert(9)
aa.insert(13)
aa.insert(20)
aa.insert(3)
aa.insert(6)
aa.insert(8)
aa.insert(10)
aa.insert(12)
aa.insert(14)
aa.insert(18)
aa.insert(25)

开始遍历：

const printCb = (value) => console.log(value)
aa.inOrderTraverse(printCb);

输出：

 

插图（方便下文排序的理解）

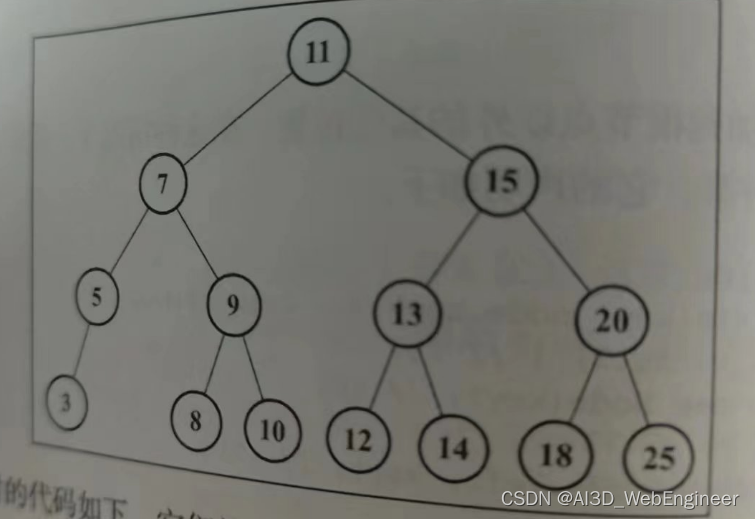
先序遍历

以优先于后代节点的顺序访问每个节点。

常用的应用场景是打印一个结构化文档。

preOrderTraverseNode(node, callback) {if (node != null) {callback(node.key);this.preOrderTraverseNode(node.left, callback);this.preOrderTraverseNode(node.right, callback);}
}

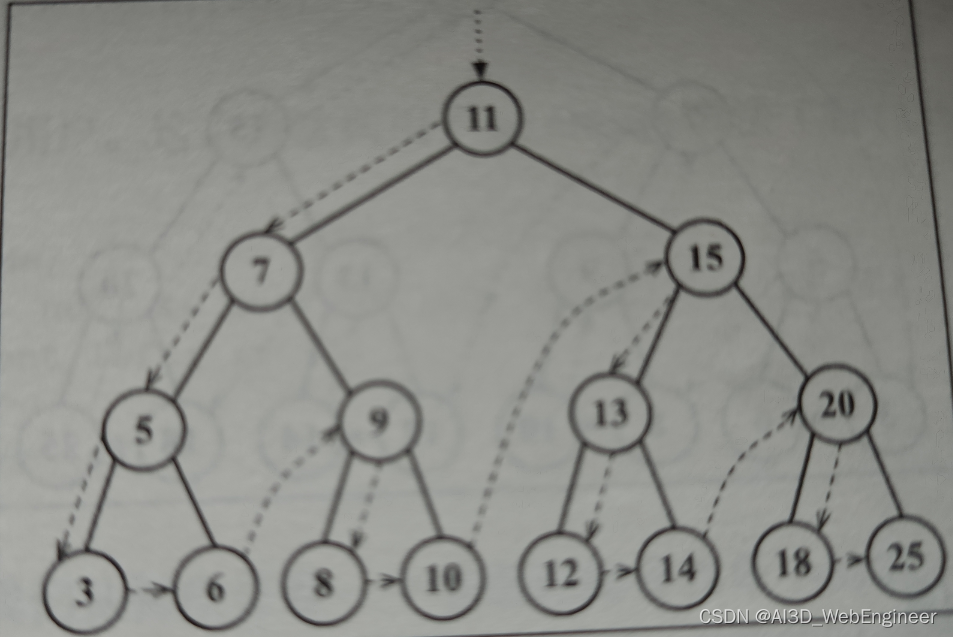
 和中序遍历不同的是：先序遍历会先访问节点本身，然后再访问它左侧的子节点，最后是右侧子节点。

  preOrderTraverseNode(node, callback) {if (node != null) {callback(node.key);this.preOrderTraverseNode(node.left, callback);this.preOrderTraverseNode(node.right, callback);}}preOrderTraverse(callback) {this.preOrderTraverseNode(this.root, callback);}

输出：11  7  5  3 6  9  8 10 15 13 12 14  20 18 25

后序遍历

后序遍历先访问节点的后代节点。再访问节点本身。

应用场景：计算一个目录及其子目录中所有文件所占空间的大小。

由上文可知，后序遍历的逻辑是：

 postOrderTraverse(callback) {this.postOrderTraverseNode(this.root, callback);}postOrderTraverseNode(node, callback) {if (node != null) {this.postOrderTraverseNode(node.left, callback);this.postOrderTraverseNode(node.right, callback);callback(node.key);}}

输出：

3 6 5  8 10  9  7 12 14 13 18 25 20 15 11

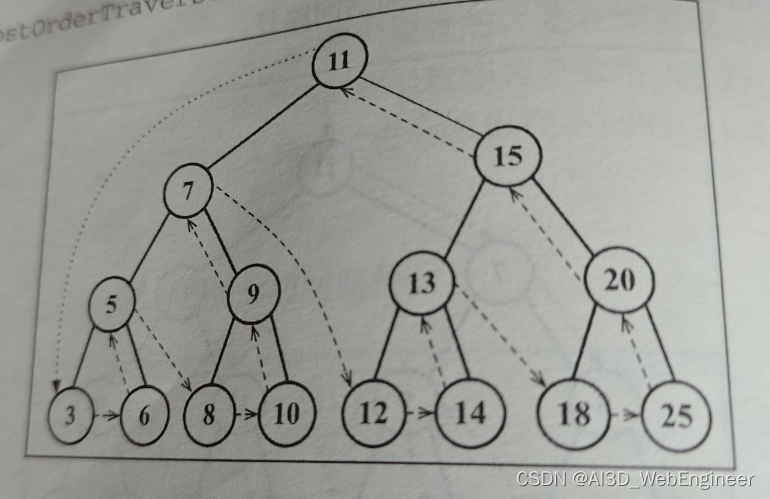
树的搜索

在树中，常用搜索有三种：

• 搜索最小值
• 搜索最大值
• 搜索特定值

我们来看看上文提到的insert方法：

insertNode(node, key) {if (this.compareFn(key, node.key) === Compare.LESS_THAN) {if (node.left == null) {node.left = new Node(key);} else {this.insertNode(node.left, key);}} else if (node.right == null) {node.right = new Node(key);} else {this.insertNode(node.right, key);}}

这里不考虑插入相等的节点值（因为这样违背了二叉搜索树的应用前提）

在学习树的搜索之前，我们必须再深刻认识一下二叉搜索树的模型。

加深认识

我们特别关注这个方法：

insertNode(node, key) if (this.compareFn(key, node.key) === Compare.LESS_THAN) {if (node.left == null) {node.left = new Node(key);} else {this.insertNode(node.left, key);}} else if (node.right == null) {node.right = new Node(key);} else {this.insertNode(node.right, key);}
}

在书写上面的实例的时候，你一定有疑惑，树的插入顺序到底会不会影响树的结果？

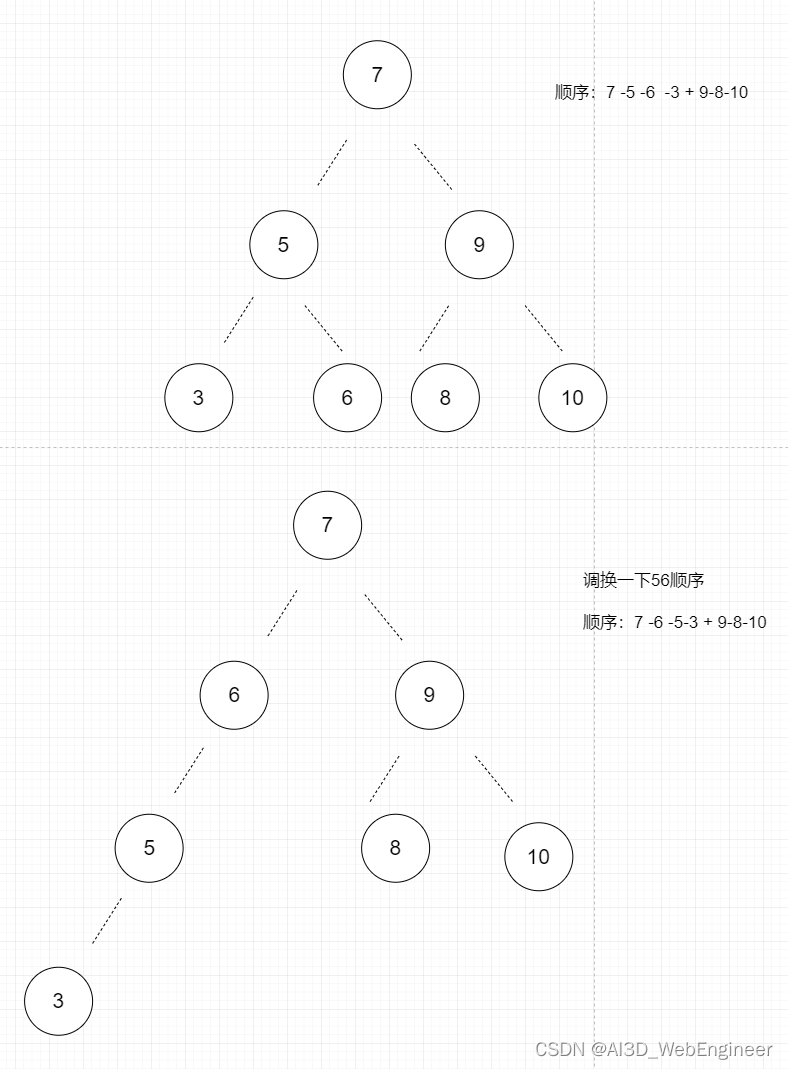
比如现在有这么个树：

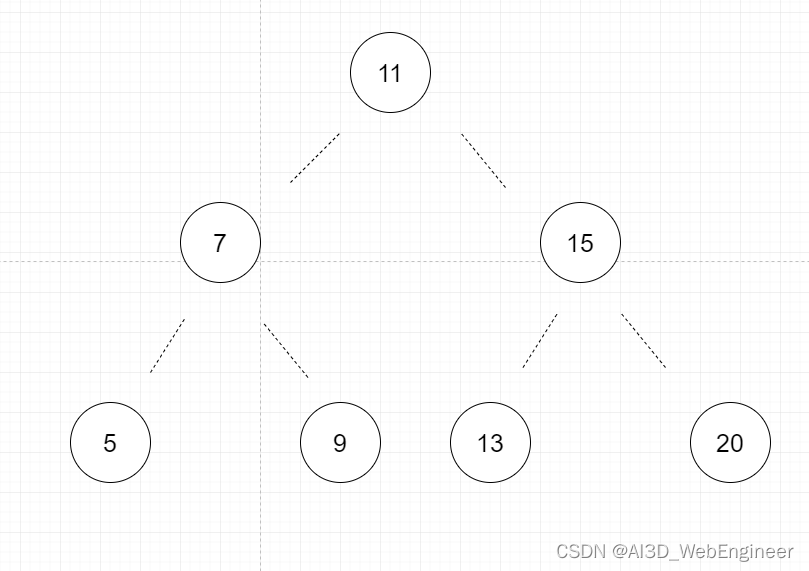
 除了顶部节点11必须第一个插入，其他的节点 7 5 9 15 13 20是否有插入顺序限制呢？

我们再仔细咀嚼代码。可知：

规律一，顶点左侧树永远小于顶点节点值。右侧永远小于顶点节点值。

 也就是左侧的树节点群（7 5  9  3  6  8 10）的顺序不会影响右侧树节点群（15 13 20）的顺序

当我们进入到下一个节点，比如插入了7之后，5  3 6的插入顺序又不会影响9  8 10...

以此，形成多个独立嵌套块

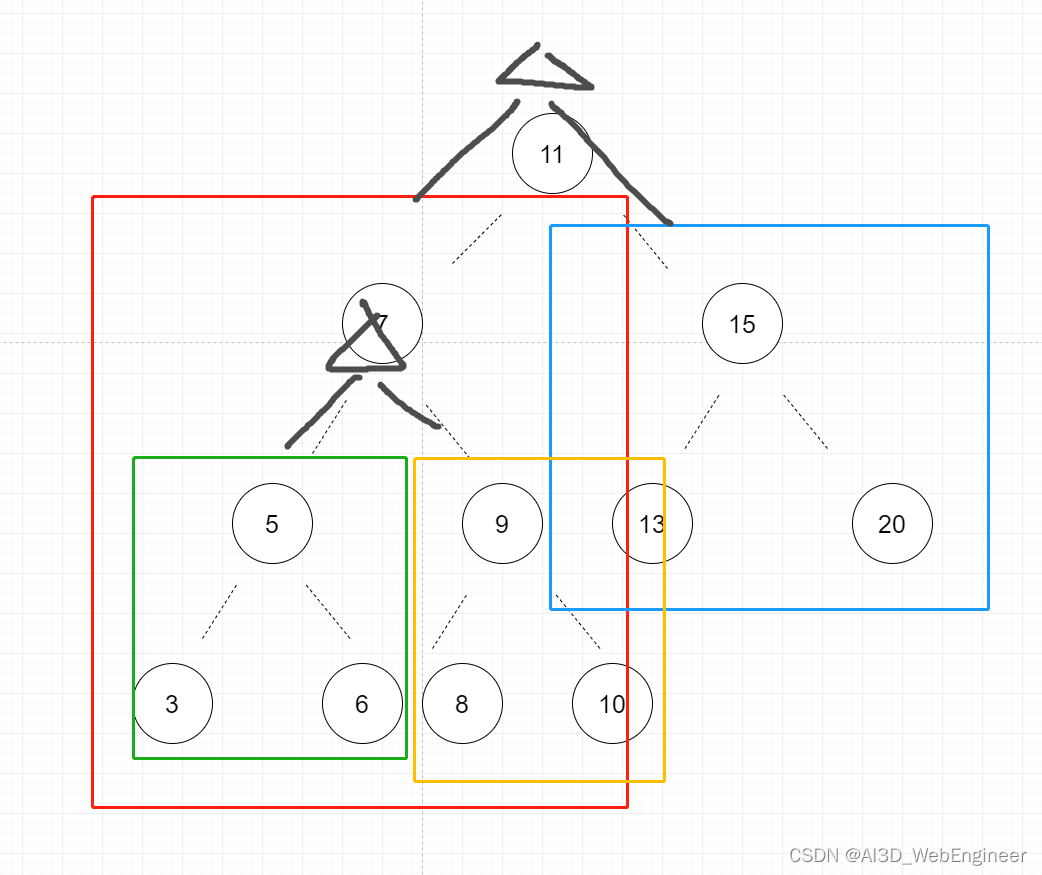
 块里面的顺序会影响树结构。比如7-5-9可以被7-6-9替代

最大值最小值搜索

 显而易见，右边大的越大，左边小得越小

所以最大值最小值我们只需要遍历找到最底部的左右侧节点值。

//  找最小键
getMin() {return  this.minNode(this.root)
}
minNode(node)   {let current  = node;while (current !=  null &&  current.left !== null ) {current = current.left}return current
}
//  找最大键
getMax() {return  this.maxNode(this.root)
}
maxNode(node)   {let current  = node;while (current !=  null &&  current.right!== null ) {current = current.right}return current
}

特定值节点搜索

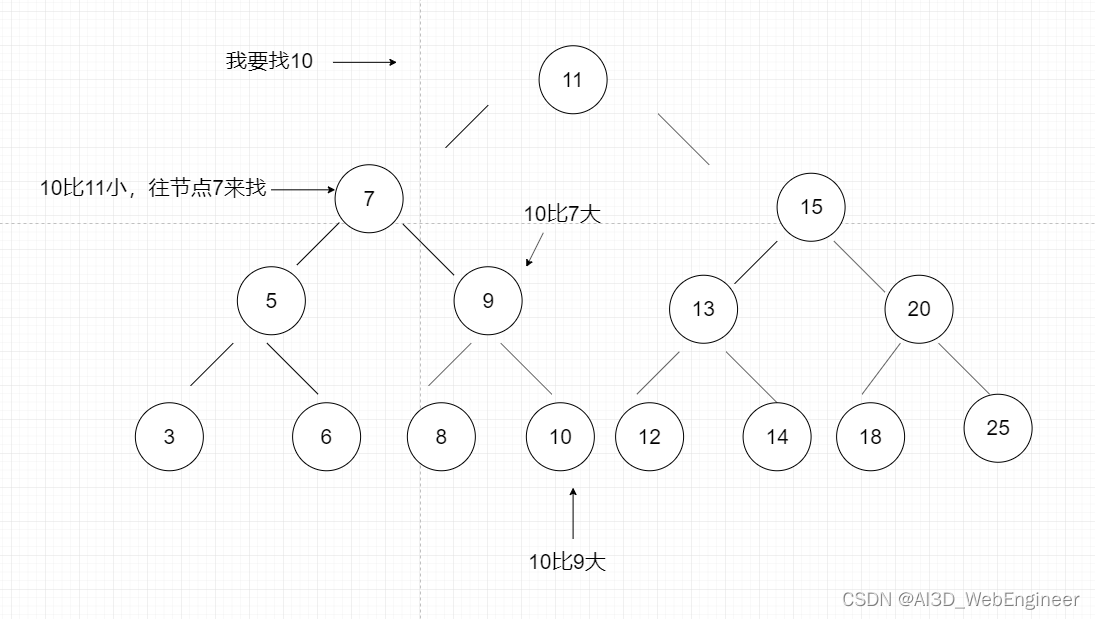
给出一个特定的节点值，我们应该如何快速地去找到他的位置呢？

还是利用二叉树的左小右大原理：

searchNode(node,key)  {if  (node == null) {//  没有找到节点return false}if (this.compareFn(key,node.key) === Compare.LESS_THAN)   {// 比它小往左边找return this.searchNode(node.left,key)}else if (this.compareFn(key,node.key) === Compare.BIGGER_THAN){// 比它大往右边找return this.searchNode(node.right,key) }else {// 找到return node}
}

移除节点

很复杂，需要认真理解。

remove(key) {this.root = this.removeNode(this.root, key);
}

这里选择将root赋值为removeNode的返回值。是理解的难点。

removeNode(node, key) {if (node == null) { // {1}return undefined;}if (this.compareFn(key, node.key) === Compare.LESS_THAN) {node.left = this.removeNode(node.left, key);return node;} else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) {node.right = this.removeNode(node.right, key);return node;if (node.left == null && node.right == null) {node = null;return node;}if (node.left == null) {node = node.right;return node;} else if (node.right == null) {node = node.left;return node;}const aux = this.minNode(node.right);node.key = aux.key;node.right = this.removeNode(node.right, aux.key);return node;
}

实现思路：

{1}如果正在检测的节点为null，则说明该键不存在于树中，返回null。

通过比大小往左下或右下找节点。当找到我们要删除的节点后。需要处理三种情况：

①移除一个叶节点（无左右子节点）

②移除有一个左侧或右侧子节点的节点

③移除有左侧和右侧子节点的节点

第①种情况是最简单的情况。

         比如我们当前要删除节点3.除了把节点3赋NULL之外，还会影响的节点只有一个。即3号节点的父节点五号节点。所以需要通过返回null来将对应的父节点指针赋予null值。

        现在节点的值是null了，父节点指向它的指针也会收到这个值。这也就是为什么我们要在函数中返回节点的值。父节点总是会接收到函数的返回值。

if (node.left == null && node.right == null) {node = null;return node;
}

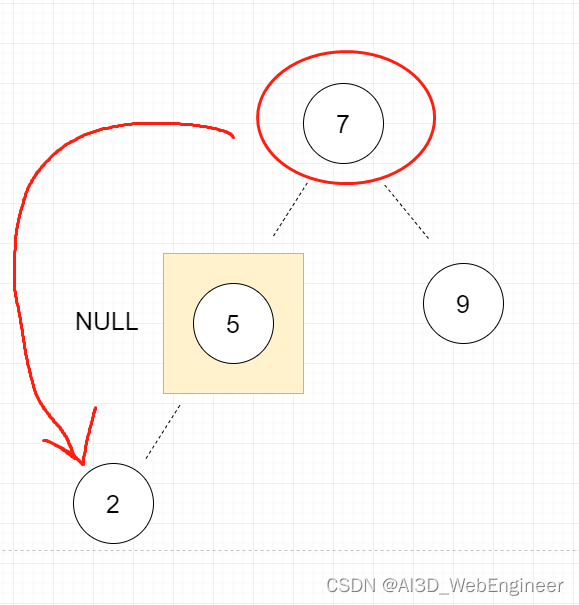
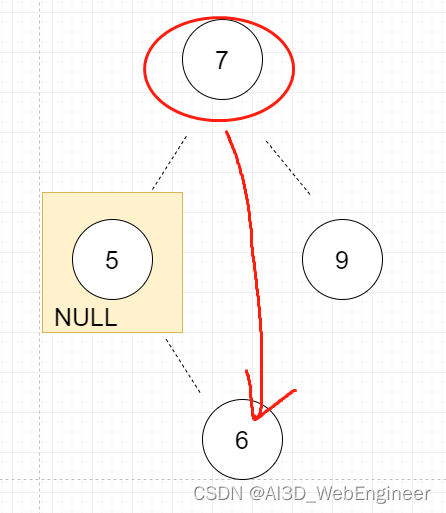
第②种情况，需要跳过这个节点。将父节点指向它的指针指向子节点。

 if (node.left == null) {node = node.right;return node;
} else if (node.right == null) {node = node.left;return node;
}

第①第②种情况摘除节点都不会影响到树的结构。第①种没子节点的不说。第②种带子节点的摘除中间节点并不会影响树节点的大小排列关系。

第③种情况，也是最复杂的情况。

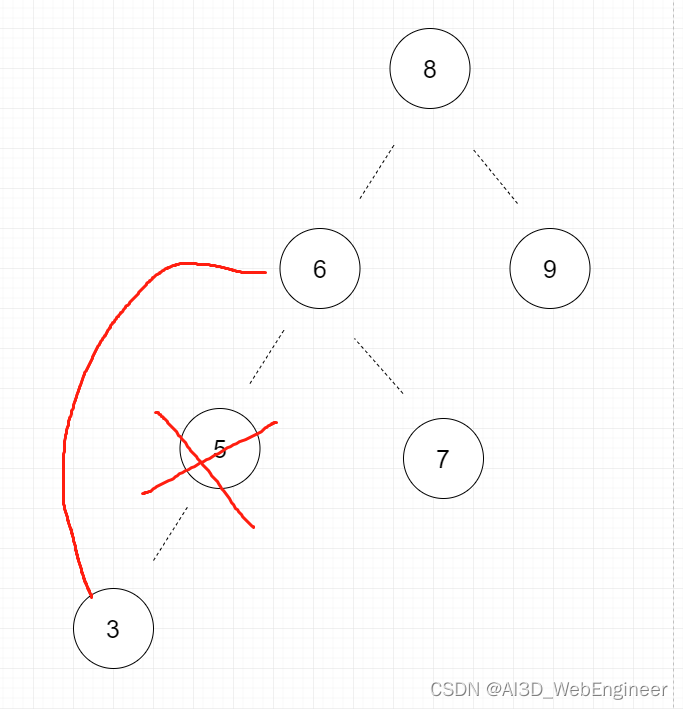
 前文已经提到了。节点的右边子节点排列并不会影响左边子节点排列。而摘掉5号节点。3<5,5<6,变成3<6也完全衔接得上。所以①②两种情况需要执行的步骤很少。麻烦的是去除的节点包含了左右子节点。

比如我们现在要删掉15节点。那么删掉15节点之后，那个节点肯定不能为null，因为它下面还挂着子节点。所以我们必须找一个子节点来替换他。

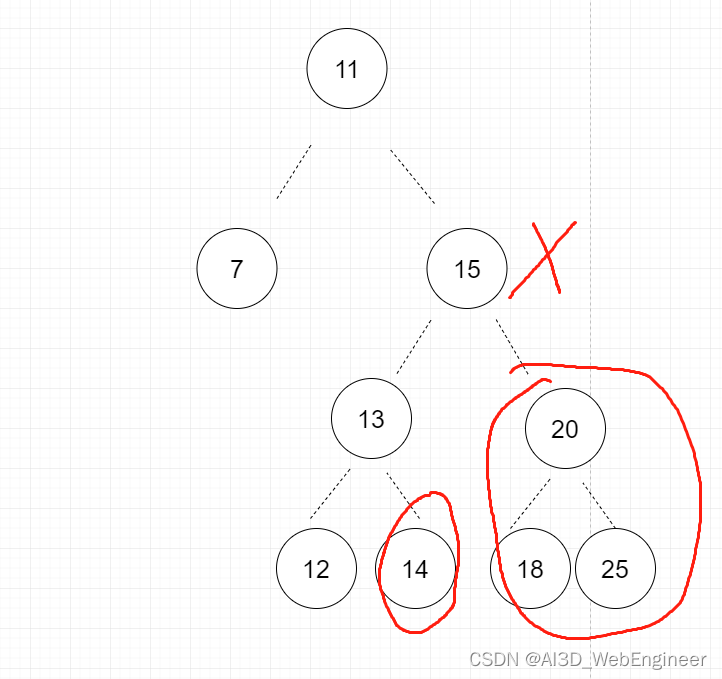
 画圈的都可以。但是13  12不行。

选13填15位置。会变成这样：

 选12，13就得放右边了，更不合理。

那么选谁来替换15呢？为了保证树的结构的统一性。我们选叶节点来替换是最好的。就剩下14 18 25 。然后我们排除25，因为25比20大。20不能作为右叶存在了。所以剩下两个：

14和18。

也就是被删除节点左子树里最大的一个。和右子树里最小的一个。那么两者都可以吗？

 在样例树上，确实可以将左子树中最大叶节点替换被删除节点。但是如果是这样：

 左侧子树没有右子树，所以最大的节点在13节点。此时与上面不同，因为13没有右侧节点，所以他可以顶替15。所以删除存在左右节点的节点。可以找他左树最大的节点和右数最小的节点。

const aux = this.minNode(node.right);
node.key = aux.key;
node.right = this.removeNode(node.right, aux.key);
return node;