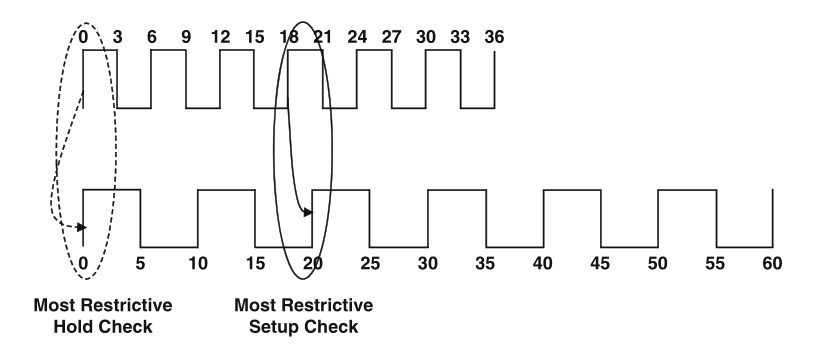
Problem


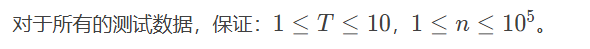
Solve
首先任意更换相邻元素任意次等同于在可交换范围内随便移动
这题是求最优解,直观想到DP和贪心,但是容易反应过来本题DP的话很难做到无后效性,且状态较多,故尝试贪心
不难发现,我们从左往右遍历的某个时刻进行交换后所得到的局部最优解总是答案的一种方案的一部分
原因很简单,我们不会因为我们为了让当前的某一列相等而做出的调度导致更加坏的结果,我们所进行的调度都会做出贡献,所以不管怎么影响后面的操作,结果都不会比啥也不干还坏
大概思路有了,现在来讲一下实现:
把每个可以随意交换的区间导出来(两列可以一起混在一个地方记录),记录其中1和0的个数,无需记录范围
导出的过程中把每个格子所属于的区间记下来,这样就可以瞬间查询所属区间的0/1储备情况
然后开始遍历每一列,采取如下步骤:
如果这一列全都被固定,直接计算
如果有一列被固定,进行调度(比如当前格子(未固定)所属区间编号为x,该去年当前与固定的格子相同的有f[x][0]个,那么f[x][0]--)
如果都没固定,看看什么元素二者区间都有,然后进行调度,如果没有就拉倒
调度成功或者匹配成功就ans++
注意,没有固定的格子在导出区间之后我们就不关心它具体的值了,我们可以认为它一定是调度来的(先假设在别的地方,再回来)
Code
#include<bits/stdc++.h>
using namespace std;
int T,n;
int f[2][100005],col;
string a,b,s1,s2;
struct p{int x,y;int sum(){return x+y;}
};
vector<p> g;
void input(){g.clear();g.push_back({-1,-1});col=1;cin>>n;getline(cin,a);getline(cin,a);getline(cin,b);getline(cin,s1);getline(cin,s2);a="#"+a;b="#"+b;s1="#"+s1;s2="#"+s2;
}
void solve1(){int cx=0,cy=0;for(int i=1;i<=n;i++){if(s1[i]=='1'){if(a[i]=='1')cx++;else cy++;f[0][i]=col;}else{if(cx||cy){g.push_back({cx,cy});col++;cx=cy=0;}f[0][i]=0;}}if(cx||cy){g.push_back({cx,cy});col++;cx=cy=0;}for(int i=1;i<=n;i++){if(s2[i]=='1'){if(b[i]=='1')cx++;else cy++;f[1][i]=col;}else{if(cx||cy){g.push_back({cx,cy});col++;cx=cy=0;}f[1][i]=0;}}if(cx||cy){g.push_back({cx,cy});col++;cx=cy=0;}
}
int solve2(){int ans=0;for(int i=1;i<=n;i++){if(!f[0][i]&&!f[1][i])ans+=(a[i]==b[i]);else if(!f[0][i]){if(a[i]=='1'){if(g[f[1][i]].x)g[f[1][i]].x--,ans++;else g[f[1][i]].y--;}else{if(g[f[1][i]].y)g[f[1][i]].y--,ans++;else g[f[1][i]].x--;}}else if(!f[1][i]){if(b[i]=='1'){if(g[f[0][i]].x)g[f[0][i]].x--,ans++;else g[f[0][i]].y--;}else{if(g[f[0][i]].y)g[f[0][i]].y--,ans++;else g[f[0][i]].x--;}}else{if(g[f[0][i]].x&&g[f[1][i]].x){g[f[0][i]].x--;g[f[1][i]].x--;ans++;}else if(g[f[0][i]].y&&g[f[1][i]].y){g[f[0][i]].y--;g[f[1][i]].y--;ans++;}else{if(g[f[0][i]].x){g[f[0][i]].x--;g[f[1][i]].y--;}else{g[f[0][i]].y--;g[f[1][i]].x--;}}}}return ans;
}
int main(){cin>>T;while(T--){input();solve1();cout<<solve2()<<endl;}return 0;
}