AGC032 VP记录

A 17:35 +0

B 39:51 +0

C 80:28 +4

A.Limited Insertion

简要题面：

最初有一个空序列，每次操作选定一个 \(i\) 并把 \(i\) 插入到位置 \(i\) ，给定最终序列，构造一种合法方案或者输出 -1 。

\(n \leq 100\)

做法：

简单思考发现每次操作出来的数一定从后往前对应了最终序列中的相同数。

这提示我们在操作的过程中我们可以实时知道当前序列中的数对应在最终序列的位置。

每次操作从后往前枚举操作决策即可。

时间复杂度 \(O(n^2)\)

B.Balanced Neighbors

简要题面：

给定一个整数 \(n\) ，构造一个 \(n\) 个点的简单无向联通图，使得每个点的邻点的点编号和相等。

$ 3\leq n \leq 100$

做法：

样例里给了 \(n=3\) 的构造，尝试手造 \(n=4\) 。

手造+打表 \(n \leq 7\) 的情况，发现都有一个合法图满足邻点编号和为 \(\frac{n(n+1)}{2} - n - [n\mod 2=0]\) 。

所以直接考虑对这个东西构造，容易发现断掉每个点的一条出边即可。

时间复杂度 \(n^2\) 。

C.Three Circuits

简要题面：

给定一个 \(n\) 个点 \(m\) 条边的简单无向联通图，判断这个图的所有边是否可以划分为三个不交的非空集合，使得每个集合内的边构成一个可以重复经过点的环。

\(n,m \leq 10^5\)

做法：

首先原图所有点的度数必须均为偶数。

接下来只需要考虑能否拉出来三个环。

这里提供两个解法，一个是 VP 时的奶龙解法，一个是更好的解法。

奶龙解法

直接跑 dfs ，每次拉出来一个不经过重复点的环，跑两遍以后看还有没有多余的边。

充分性易证，必要性完全没有。

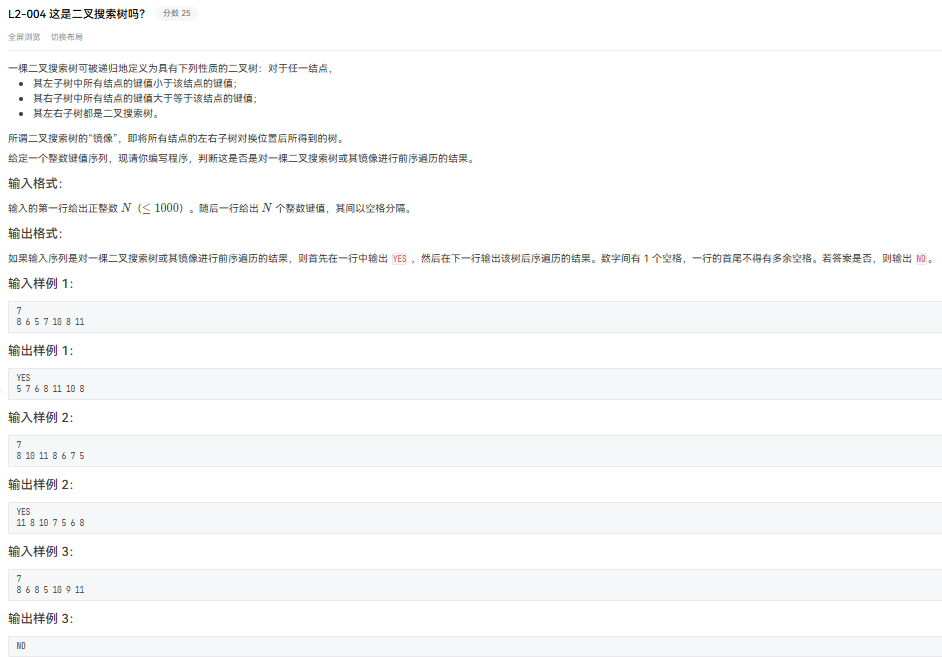
容易发现以下图片中的图便是一个必要性的反例。

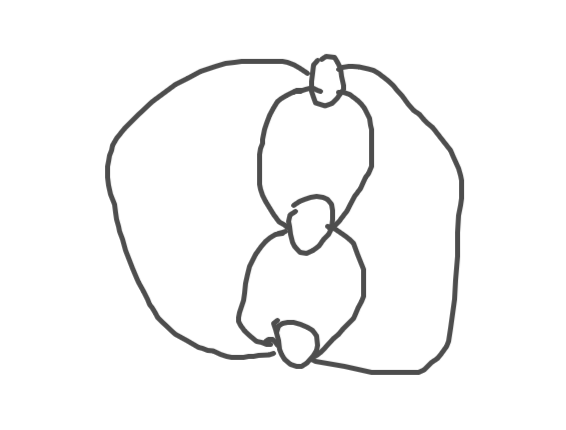
解决这个问题也比较容易，直接随机选出边跑 10 次就行了！

时间复杂度 \(O(Tn \log n)\) ，\(T\) 为跑的次数，log 是因为删边比较麻烦所以用 set 维护导致的。

更好的解法

首先图内如果有一个节点度数大于等于 6 ，从这个点拉出来三个环就行了。

所以还不合法的图所有点的度数不超过 4 。

显然有至少三个度数为 4 的节点合法。

恰好两个的情况比较特殊，需要判是否拉出一个环出来会使得图不联通。

时间复杂度 \(O(n)\) 。

D.Rotation Sort

简要题面：

给定一个长度为 \(n\) 的排列 \(p\) 和两个整数 \(a,b\) ，每次操作可以消耗 \(a\) 的代价把某个数向后插入到任意位置或者消耗 \(b\) 的代价把某个数向前插入到任意位置，问把整个序列变为升序的最小代价。

\(n \leq 5000, 1\leq a,b \leq 10^9\)

解法：

容易发现每个数只会被操作一次，同时决策了每个数被操作的方向以后我们就不关心这个数原本的位置了，只需要保证每个数可以被操作到合法位置即可。

设计 dp ，令 \(f_{i,j}\) 表示前 \(i\) 个数中最后一个没有被操作的数为 \(j\) 的可以使这个前缀合法的最小代价。

转移是简单的，如果固定的数较小就往后移或者不动，否则就必须往前移。

时间复杂度 \(O(n^2)\)

E.Modulo Pairing

简要题面：

给定 \(n,m\) 与一个长度为 \(2n\) 的整数序列 \(a\) ，决策一种匹配，使得每个数正好与另一个数匹配，同时每对匹配的数的和 \(\mod m\) 的最大值最小。

\(n \leq 10^5, 1\leq m\leq 10^9, 0\leq a_i < m\)

做法：

非常厉害调整。

参考了 粉兔的题解 。

先把 \(a\) 排序。

如果把和小于 \(m\) 的匹配连蓝边，大于等于 \(m\) 的匹配连红边，最终的答案一定形如某个前缀中都是蓝边的匹配，且最大和最小依次匹配，后缀中都是红边且最大和最小依次匹配。

证明和匹配的形式粉兔的题解中有很清晰的图片。

知道了这个结论之后就可以二分边界点了，因为靠左的分界点答案更小，合法的分界点一定是一个后缀。

这意味着我们可以二分，时间复杂度 \(O(n\log n)\)

F.One Third

非常恐怖推式子，回家补。