- 引
- 线性量化 (Linear Quantization)
- 对称量化
- 非对称量化
- 非线性量化
- Power-of-X
- Rounding
- Deterministic rounding
- Stochastic rounding
[1] 进击的程序猿-模型压缩-神经网络量化基础.
[2] Przewlocka-Rus D., Sarwar S. S., Sumbul H. E., Li Y. and De Salvo B. Power-of-two quantization for low bitwidth and hardware compliant neural networks. tinyML Research Symposium, 2022.
[3] Li Y., Dong X. and Wang W. Additive powers-of-two quantization: an efficient non-uniform discretization for neural networks. ICLR, 2020.
[4] Xia L., Anthonissen M., Hochstenbach M. and Koren B. Improved stochastic rounding. 2020.
引
整理了一下量化中的基础概念和方法. 其实, 在计算机中, 我们所见之浮点数也只不过是真正数字的一个高精度量化 (e.g, FP32), 但是随着模型的逐步增加, 我们需要将模型进一步'精简'. 当然了, '精简'的法子有很多: 裁剪 (pruning), 蒸馏 (distillation), 包括这里讲到的量化 (quantization). 个人感觉, 相较于裁剪和蒸馏, 量化是一种即插即用的方法 (虽然会有一些追求极限精度的量化方法需要一些校准). 本文讨论如下的例子:
线性量化 (Linear Quantization)
对称量化

-
\(x_q = Q(x_f)\) 的对称量化过程如下:
- 确定 \(x_f\) 的(绝对值)范围: \(\Delta_f = \max_i(|x_f[i]|)\);
- 确定 \(x_q\) 的范围: \(\Delta_q = 2^{N-1} - 1\), \(N\) 表示量化后的精度, 比如 Int8 时 \(\Delta_q = 127\).
- 量化:\[x_q = Q(x_f) := \text{round}(\frac{x_f}{\Delta_f} \cdot \Delta_q). \]
-
如上图所示, \(\Delta_f\) 首先将 \(x_f\) 压缩到 \([-1, 1]\) 之中, 然后再映射回 \([-128, 127]\) 的量化后的精度中.
def quant(f: torch.Tensor, N: int = 8):delta_f = f.abs().max()delta_q = 2 ** (N - 1) - 1return (f * delta_q / delta_f).round().to(torch.int), delta_f- 利用上述代码可得:
- 反解的过程:\[\hat{x}_f = Q^{-1}(x_q) := \frac{x_q}{\Delta_q} \cdot \Delta_f. \]
def dequant(q: torch.Tensor, delta_f: torch.Tensor, N: int = 8):delta_q = 2 ** (N - 1) - 1return (q * delta_f / detal_q).float()- 得到:\[[-3.1000, -0.0244, 0.0976, 1.1961]. \]
非对称量化

-
\(x_q = Q(x_f)\) 的非对称量化过程如下:
- 确定 \(x_f\) 的(绝对值)范围: \(\Delta_f = x_f^{\max} - x_f^{\min}\);
- 确定 \(x_q\) 的范围: \(\Delta_q = 2^{N} - 1\), \(N\) 表示量化后的精度, 比如 UInt8 时 \(\Delta_q = 255\).
- 确定零点偏移量: \(x_{offset} = -x_f^{\min}\)
- 量化:\[x_q = Q(x_f) := \text{round}(\frac{x_f + x_{offset}}{\Delta_f} \cdot \Delta_q). \]
-
注意到:
\[x_f + x_{offset} = x_f - x_f^{\min} \in [0, \Delta_f]. \]
def quant(f: torch.Tensor, N: int = 8):offset = -f.min()delta_f = f.max() + offsetdelta_q = 2 ** N - 1return ((f + offset) * delta_q / delta_f).round().to(torch.int), delta_f, offset-
通过如上代码可得量化结果:
\[[0, 182, 190, 255] \] -
通过如下方式进行反解:
\[\hat{x}_f = Q^{-1}(x_q) := \frac{x_q}{\Delta_q} \cdot \Delta_f - x_{offset}. \]
def dequant(q: torch.Tensor, delta_f: torch.Tensor, offset: torch.Tensor, N: int = 8):delta_q = 2 ** N - 1return (q * delta_f / delta_q).add(-offset).float()- 得到:\[[-3.1000, -0.0310, 0.1039, 1.2000] \]
非线性量化
-
其实, 一般的量化都可以用如下的过程统一表示:
- 将 \(x_f\) normalize 到 \(\phi(x) \in [0/-1, 1]\) 区间内;
- 在该区间内设置 \(2^N\) (或者 \(2^N - 1\)) 个点, 记为:\[\mathcal{Q} = \{q_i\}_{i \in \mathcal{I}}. \]
- 寻找最近邻的作为量化结果:\[Q(x) = \mathop{\text{argmin}} \limits_{i \in \mathcal{I}} |\phi(x) - q_i|. \]
-
之前的线性量化实际上就是:
\[\mathcal{Q} = \{i / (2^{N - 1} - 1)\}_{i \in \mathcal{I}}, \\ \mathcal{I} = \{-(2^{N-1} - 1), \ldots, 0, 1, \ldots, 2^{N-1} - 1\}, \]和
\[\mathcal{Q} = \{i / (2^{N} - 1)\}_{i \in \mathcal{I}}, \\ \mathcal{I} = \{0, 1, \ldots, 2^{N} - 1\}. \] -
而 round 就是一种自动的 nearest 的搜索方式.
-
当然了, \(\mathcal{Q}\) 的分布不必像线性量化一样那样的均匀, 实际上这种分布往往不是最优的. 容易感觉到, 最优的分布应当在 \(x_f\) 中比较稠密的范围分布较多的量化点, 否则会造成大量的浪费. 当然了, 这种非线性量化的方式相较于线性量化有它的不足之处, 就是得根据数据'找'一个合适的分布, 这个'找'的过程往往是比较耗时的.
Power-of-X
-
Power-of-X 的特点就是 \(\mathcal{Q}\) 的分布是服从指数分布的:
\[\mathcal{Q} = \{\alpha^{i-1} \}_{i \in \mathcal{I}} \cup \{\mathcal{Q}_0 = 0\}, \\ \mathcal{I} = \{1, \ldots, 2^{N} - 1\}. \]其中 \(\alpha \in (0, 1)\).
-
其量化过程为:
- 确定 \(x_f\) 的(绝对值)范围: \(\Delta_f = \max_i(|x_f[i]|)\);
- 确定 \(x_q\) 的范围: \(\Delta_q = 2^{N-1} - 1\), \(N\) 表示量化后的精度, 比如 Int8 时 \(\Delta_q = 127\).
- 量化:\[x_q = Q(x_f) := \text{sign}(x_f) \cdot \text{clip} \Bigg( \text{round}\bigg(\log_{\alpha} \bigg(\frac{|x_f|}{\Delta_f}\bigg) + 1 \bigg), 0, \Delta_q \Bigg). \]
- 反解的过程为:\[\hat{x}_f = \text{sign}(x_q) \cdot \alpha^{|x_q| - 1} \cdot \Delta_f. \]
注: 这里 \(+1, -1\) 是为了将 \(0\) 保留给真正的 0 值.
def quant(f: torch.Tensor, alpha: float, N: int = 8):sign, f = f.sign(), f.abs()delta_f = f.max()delta_q = 2 ** (N - 1) - 1logalpha = math.log2(alpha)return (f / delta_f).log2().div(logalpha).add(1).round().clip(0, delta_q).mul(sign).to(torch.int), delta_fdef dequant(q: torch.Tensor, alpha: float, delta_f: torch.Tensor, N: int = 8):sign, q = q.sign(), q.abs()return (alpha ** q.add(-1)).mul(delta_f).mul(sign)
-
如上图所示, \(\alpha \rightarrow 0\), 不均匀性大大增加. 这个性质在有些时候会很有用, 因为很多数据的分布是形容高斯分布的, 此时采用不均匀的会更加高效.
-
需要声明的一点是, \(\alpha \rightarrow 1\) 的时候, 整体会显得更加均匀一点, 但是并不能等价线性量化, 注意到:
\[\alpha^{2^N} \mathop{\longrightarrow} \limits^{\alpha \rightarrow 1} 1. \]这意味着, 除了 \(0\) 之外, \(\mathcal{Q}\) 所能表示的最小值会随着 \(\alpha\) 增加逐步增大. 这其实是另一种极为严重的 '不均匀' 性质.
-
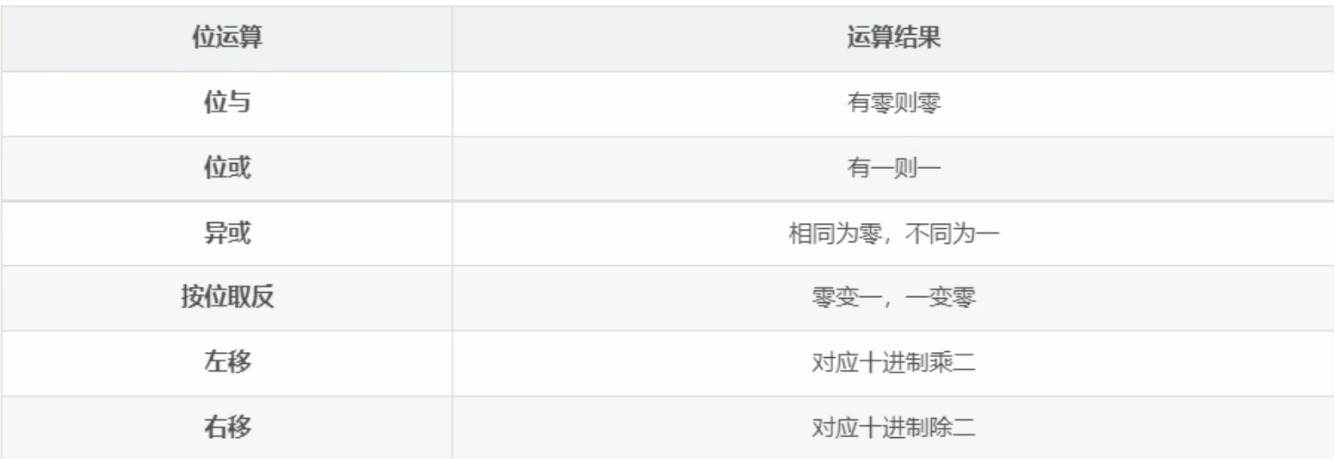
此外 \(\alpha = 0.5\) 是比较特殊的一种情况, 可以通过位操作加速.
Rounding
有些时候 Rounding 的方式也很重要, 毕竟它是误差的来源.
Deterministic rounding
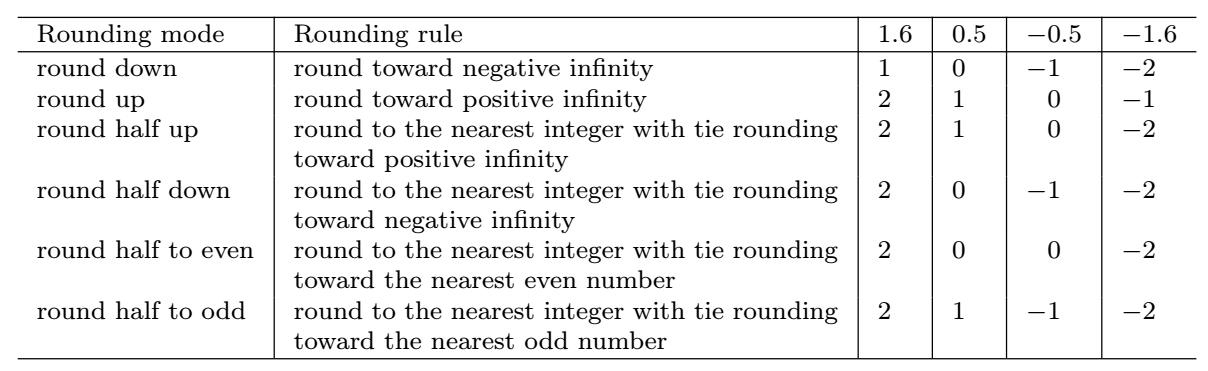
Stochastic rounding
-
随机 rounding 形式如下:
\[\text{round}(x) = \lfloor x \rfloor + \mathbb{I}\big[x - \lfloor x \rfloor \xi \big], \quad \xi \sim \mathcal{U}([0, 1]). \]其中 \(\lfloor x \rfloor\) 表示 round down 操作.
-
举个例子, 对于 \(0.4\), 它有 0.4 的概率为 \(1\) 有 \(0.6\) 的概率为 0. 对于 \(-1.6\), 它有 \(0.6\) 的概率为 \(-2\), 有 \(0.4\) 的概率为 \(-1\).
-
一个比较好的性质是:
\[\begin{array}{ll} \mathbb{E}[\text{round}(x)] &= \lfloor x \rfloor + \mathbb{E}\bigg[\mathbb{I}\big[x - \lfloor x \rfloor \xi \big] \bigg] \\ &= \lfloor x \rfloor + 1 \cdot (x - \lfloor x \rfloor) \\ &= x \end{array}. \]