1. CDCL伪代码
CDCL(CNF):副本 = CNF // 创建CNF的副本,不更改原CNFwhile true:while 副本含有单位子句:对副本使用单位传播;if 副本中含有取值为假的子句: // 发现冲突if 现在的决策层是0:return false; // 不能满足C = 子句学习(CNF, 副本) // 吸取教训根据C回到一个更早的决策层; // 调整策略else:if 所有变量都被赋值:return true; // 可满足else: // 进行一次决策(决策就是一次尝试,令某个文字为真,撞大运)开始一个新的决策层;找到一个未赋值的文字l;副本 = 副本∧{l}// 给l赋值为真// 加入l构成的单位子句,使得副本要满足就是l要满足,变相地要求l为真// 对于变量x,若给x赋值为真,就令l = x;若给x赋值为假,就令l = ¬x
2. 迹(Trail)与决策层
2.1 迹(Trail)
迹的作用是记录当前变元的赋值是怎么被推断出来的。迹是一串连在一起的文字,里面出现的每个文字代表这个文字赋值为真;同时我们要记录为什么这个文字赋值为真,于是在文字的右上角标注原因。当文字是因为决策取真时,我们就标“决策”;当文字因为副本中的某个子句而被迫取真时,我们就标注这个子句。
2.2 决策层
决策层是指通过某种策略H(x)挑选出一个还未赋值的变元,对它进行赋值(moms策略及satz中up探测挑选出来的变元,都可以说是决策层),即变元的赋值不是由单子句传播(UP)推断出来的。
2.3 例子
^0dbd6b
有下面一个迹:
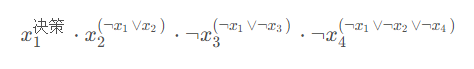
首先\(x_1\)在第一次决策中被赋值为真,在cnf中又有子句\(\lnot x_1 \lor x_2\),为了使这个子句为真可以推断出\(x_2\)的值为真,于是我们在\(x_2\)右上角标注推断出\(x_2\)值的这个句子,依次类推,因cnf中含有子句\(\lnot x_1 \lor \lnot x_3\),其中\(x_1\)在第一次决策时已经被赋值为真,为了使这个子句为真,\(\lnot x_3\)就必须为真,于是我们在\(\lnot x_3\)的右上角标上子句\(\lnot x_1 \lor \lnot x_3\),最后的\(\lnot x_4\)也是同样的道理。
2.4 根据[[CDCL#^0dbd6b|1.3的例子]]可以推导出迹的维护规则
- 如果算法做出决策使文字\(l\)为真,那么在迹的末尾添加\(l^{\text{决策}}\)
- 如果子句\(C = \{l_1 \lor l_2 \lor l_3 \lor l_4 \lor ... \lor l_k \lor l\}\)因单子句传播导致\(l_1 \lor l_2 \lor l_3 \lor l_4 \lor ... \lor l_k\)都为假时,为了使子句\(C\)为真,文字\(l_k\)就只能取真,那么就在迹的末尾加上\(l^C\)
- 如果算法回溯了,那么我们将相关的元素从迹的末尾删除
根据上述规则,可以得出:
1、一个迹中决策层的数目是该迹中文字右上角标有决策的个数;
2、从一个右上角标有决策的文字开始(包含该文字)到下一个右上角标有决策的文字之前(不包含该文字)所有的文字都属于同一个决策层,且右上角标有决策文字之后的所有文字的值都是该决策文字推导出的(直接或者间接导致的);
3. 蕴含图(Implication Graph)、子句学习和回溯
- 原贴
4. 分支策略
4.1 VSIDS(Variable State Independent Decaying Sum)
- 每个文字有一个计数器,记录该文字在子句集中出现的次数,初始为 0;
- 每当一个子句添加到子句集中,该子句中所有文字的计数器均增加;
- 每次分支选择未赋值且计数器最高的文字进行赋值;
- 在有多个相等计数器的情况下,随机选择一个文字进行赋值;
- 周期性地,所有文字的计数器均除以一个常数。
4.2 VSIDS 策略的延伸
这些策略为每个变量(而不是文字)设置一个计数器,称为得分,初始为 0。另一方面,当搜索遇见冲突并产生学习子句时,不仅增加学习子句中变量的得分,而是将与冲突分析过程有关变量的得分都增加。另外,每隔一个周期,所有变量的得分均乘以一个浮点数\(\alpha(0 \lt \alpha \lt 1)\),因此不经常出现在最新学习子句中的变量的得分就会降低。
4.2.1 EVSIDS 策略(Exponential VSIDS)
EVSIDS 策略在每次发生冲突时将与冲突有关变量的得分增加 \(g^n\),其中\(g=\frac 1f (0\lt f \lt 1)\) ,n为目前发生的冲突次数,其它与该冲突无关的变量得分保持不变。显然,\(g^n\)是一个与冲突有关的变量,并且随着冲突次数的增加而逐渐增加,这样就能优先考虑最新的学习子句。
优点:\(g^n\)是一个与冲突有关的变量,并且随着冲突次数的增加而逐渐增加,这样就能优先考虑最新的学习子句。
4.2.1 ACIDS(Average Conflict Index Decision Score)
与 EVSIDS 一样,ACIDS 策略为每个变量设置一个计数器,称为得分,不同的是每次发生冲突并产生学习子句时,与冲突有关变量的得分更新为\(\frac {s+n}2\),其中 s 为冲突之前变量的得分,n 为目前发生的冲突次数,与冲突无关的变量得分保持不变。
优点: ACIDS 策略不仅优先考虑最新发生的冲突,而且使较早发生的冲突对搜索的影响随着冲突次数的增加呈指数阶下降,这是因为学习子句的作用会随着搜索的进行而减小。
5. 学习子句删除策略
5.1 基于子句活性的删除策略
求解器BerkMin的作者提出一种基于子句活性的学习子句删除策略。学习子句被存储在一个后进先出的栈中,因此最新的学习子句将处于栈顶的位置,称为栈顶子句。根据学习子句在栈中的位置,将学习子句大致分为新子句和旧子句两类,新子句指的是从栈顶子句开始整个栈的前\(15 \over 16\)的子句,其他的子句称为旧子句。另外,每个学习子句设有一个计数器,存储与该学习子句有关的冲突次数,称为子句活性。求解器 BerkMin 删除的学习子句可分为以下三部分:
- 已经满足的学习子句;
- 子句长度大于 42 并且子句活性小于 7 的新子句;
- 子句长度大于 9 并且子句活性小于临界值的旧子句(BerkMin 的实现中临界值初始设为 60,并逐渐递增)。
求解器 BerkMin 根据子句活性和子句长度删除学习子句,子句活性反应了该学习子句对之前发生的冲突的贡献,子句长度短的学习子句将不会根据子句活性被删除,而是一直被保留。
5.2 基于 LBD 的删除策略
该策略由 Glucose求解器的作者提出,定义如下:
设C 是一个子句,P 是根据当前赋值对子句C 中文字的一个划分,划分P将子句C中的文字按照决策层划分为n个子集,则子句C的LBD为n 。
例子:
设有子句\(C=x_1 \lor x_2 \lor x_3 \lor x_4\),如果\(x_1,x_2,x_3,x_4\)所属的决策层分别是2,2,3,4,则该子句的LBD值为3。
一个学习子句的 LBD 值反应出为了得到该学习子句而做出的决策次数,LBD 值越大,决策次数越多。不难看出,LBD 值为 2 的学习子句是很重要的。并且大量的实验表明,在冲突分析和布尔约束传播过程中,LBD 值小的学习子句比 LBD 值大的学习子句使用的次数更多,因此更为重要。求解器 Glucose 实现的学习子句删除策略描述如下。每当产生一个学习子句,计算相应的 LBD 并保存。无论原子句集的大小,每隔\(20000+500*x\)次冲突就删除50%的学习子句,其中x指此次子句删除之前已经执行的子句删除的次数。LBD 大的子句被删除,而 LBD 小的子句将被保留。
6. lazy数据结构
主要思想:将操作向后延迟或者操作执行不完全。
例如:cdcl中vsids策略每次决策的时候需要取出的分最高的自由变元,而每个变元的得分也在动态变化,我们可以使用一个优先队列,这样我们就不用每次遍历一遍整个变元的得分情况,找到得分最大的那个变元,从而降低了时间复杂度。但是在单子句传播的过程中,可能会有很多的变元被赋值,所以我们就需要进行一个操作,将那些已经不是自由变元的变元从队列中删除,这个时候我们并不需要立即调整优先队列,而是等到下一次决策的时候直至取到一个为自由变元的堆顶元素(如果堆顶元素为非自由变元,将其从队列中删除),这样就相当于把这个操作向后延迟了。当然,从堆顶取出决策变元后,优先队列中依然存在非自由变元,这也是上面说的操作不完全。
想想上面这个例子的这种延迟操作有什么好处?如果在单子句传播的过程中,一个变元的值被推断出来,我们立即将这个变元从优先队列中删除,并且此次单子句传播产生了冲突,那么我们就需要回溯,回溯又会导致我们需要将这些被删除的变元重新放回队列中,这样就会增加时间开销。而放到从堆顶元素取决策变元的时候,再将已经不是自由变元的变元进行删除,并且可以顺便找到决策变元(如果是自由变元也就是我们要找的决策变元),一举两得。
6.1 two laterals watched(2WL)
对于一个子句,我们只用对其中的两个文字进行监督(相当于没被监督的文字不可见),就能知道这个子句满足情况
- 当其中一个被监督的文字值为假时
- 如果另外一个被监督的文字值为真,该子句已经满足,不用做什么操作
- 如果另外一个被监督的文字还没有赋值,且找不到另外可监督的文字了(即其余未被监督的文字取值全为假),那么此子句已经成为一个单子句,可以进行单子句传播
- 如果另外一个被监督的文字还没有赋值,但是可以找到重新监督的文字(取值为非假的文字),那就取消对之前文字的监督,重新监督找到的文字
- 如果另外一个被监督的文字值也为假,且找不到另外可监督的文字了,那么此子句已经成为了一个空子句,即产生了冲突
7. 重启技术
在CDCL算法中应用非时序回溯后,导致分支搜索深度差异巨大,部分分支深度过大,这种现象称为重尾现象。通俗来说,就是求解器在求解的过程中,可能会陷入一片无解的空间,从而浪费许多时间,这时候我们可以通过采取”重启“的方式,回溯到决策层的第0层(第0层变元的赋值已经确定,重新从第1决策层开始决策),即决策树根部的位置,并且保留冲突之后加入进来的学习子句,以及其他的信息,利用这些信息,重新构造决策树,从而避免在本身无解的空间里花费太多的搜索时间。
一次重启如下:
- 停止求解过程
- 重新构建决策树,清除所有文字的赋值
- 保留整个子句库,包括原始子句、冲突产生的子句和蕴含推导子句
- 重新分支决策和文字赋值
7.1 主要的重启策略
7.1.1 固定间隔重启策略
最初的重启策略,通过统计回溯的次数进行重启,采用固定间隔进行重启,每次冲突数达到该数目进行一次重启。
- Siege 求解器每隔 16000 次冲突调用一次重启,表示为(16000, 1)
- zChaff 求解器每隔 700 次冲突调用一次重启,表示为(700, 1)
- BerkMin 求解器每隔 550 次冲突调用一次重启,表示为(550, 1)
7.1.2 几何序列调度策略
几何序列调度策略值在求解过程中,冲突数积累按照几何调度序列公式变化而进行重启的一种策略。设置一个初始值作为初始重启间隔,之后每次间隔序列呈现几何级数增加,通常这个级数为 1.5。
例如:设置初始重启间隔为 200 次冲突,则初始间隔\((limit,l)\ l=200\),随后\(l_{n+1} = l_n*1.5\),即表现为形如200, 300, 450……的几何序列,表示为\(G(200,1.5)\)。
固定间隔的冲突数列可以表示成一个公差为 0 的等差数据;几何序列调度策略产生的冲突数列就是一个公比为 1.5 的等比数列。
7.1.3 Luby序列重启策略
无限循环序列 Luby-sequence 由 Luby 于 1993 年提出并应用,是增量序列调度策略中的一种序列,已被证明为未知随机搜索空间的最佳调度方法。表现为:
1
1 1 2
1 1 2 1 1 2 4
1 1 2 1 1 2 4 1 1 2 1 1 2 4 8
......
其序列用公式可以表现为:
SAT 求解过程中,每产生一个冲突的时候是没有必要进行回溯的,因此,在实际应用中,这个序列被乘以一个因子得到一个新的序列,作为重启序列。这个因子被称为单元运行因子\((Unit\ Run,u)\)。
重启策略表示为\((Luby, u)\),即第 i 次重启间隔积累的冲突次数为\(u*t_i\)。
例如 \(Luby(16)\),u = 16 时,重启序列表现为:16,16,16,32,16,16,32,16,16,32,64,......
8. 子句化简
8.1 recursive clause minimization

一句话总结rcm就是:如果子句中的某个文字的值在蕴含图中是被该子句中其他文字所推导出的,那么该文字就能够被简化掉。