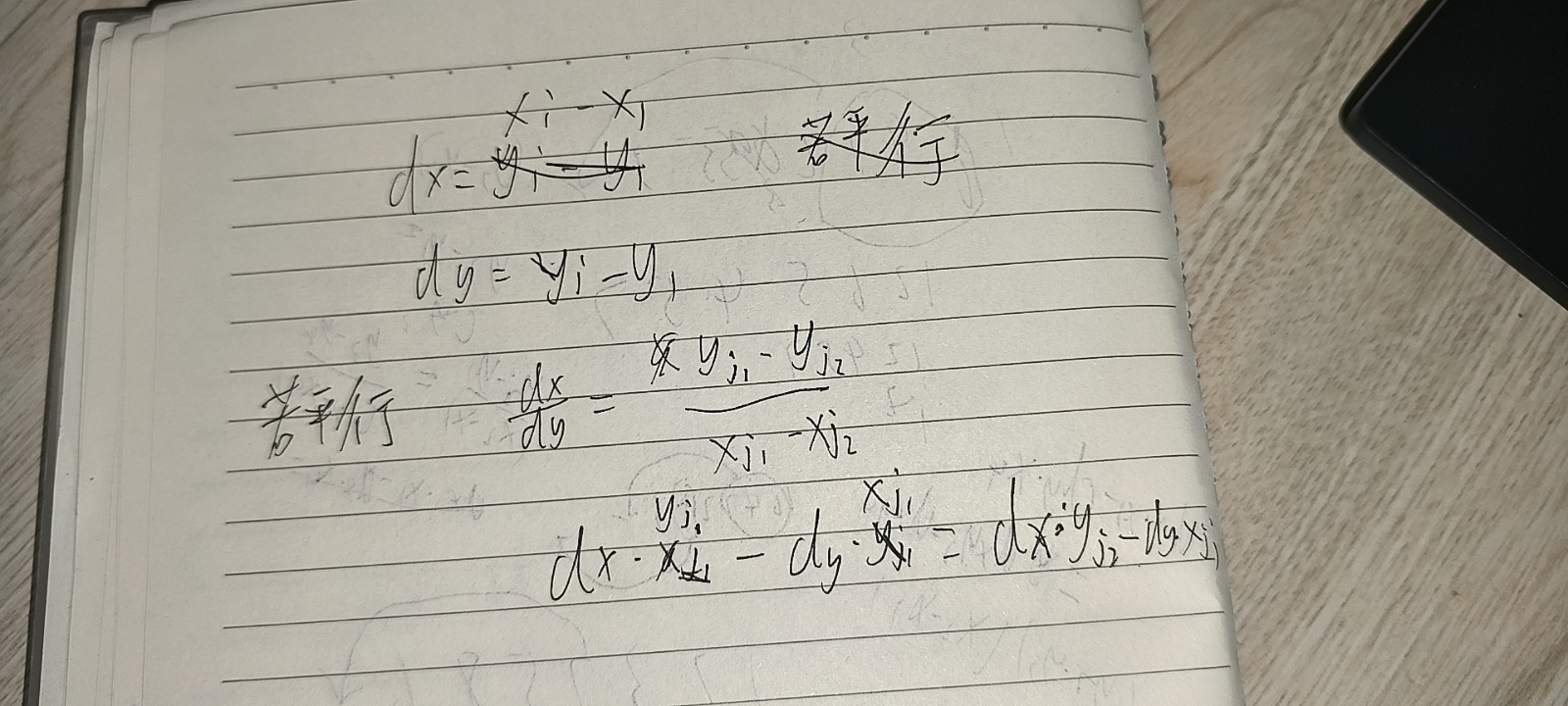acwing语法基础课总结（未完结）

news/2024/12/5 1:17:08/文章来源:https://www.cnblogs.com/PeachyGalaxy/p/18540310/1205p

题单
https://www.acwing.com/activity/content/10/

1>基础概念

权重(609)

和比列不同，例如

A的成绩是90，权重为3.5；B的成绩是95，权重是7.5

平均成绩就是(90 * 3.5 + 95 * 7.5) * 1.0 / (3.5 + 7.5)

pow函数

返回值类型为double类型

取整函数

ceil函数
向上取整
头文件 cmath
返回值是double类型
double a = ceil(x);
int b = (int) ceil(x);
floor函数
向下取整
头文件 cmath
返回值类型double
double a = floor(x);

isdigit函数

判断一个字符是否为数字字符，是数字则返回非0值
头文件cctype

find_first_of函数

string s; cin >> s;
s.find_first_of("01");  //在s字符串中寻找最先出现的括号中字符串的字符，返回下标；本例中寻找1或者0，看谁先出现就返回谁的下标

sort函数

对数组进行排序
sort(a, a + n);
对容器进行排序
sort(a.begin(), a.end());

去重

a.erase(unique(a.begin(), a.end()), a.end());

大写转小写

处理整个字符串

<algorithm>
<cctype>
transform(str.begin(), str.end(), str.begin(), tolower);

处理单个字符

<cctype>
str[i] = tolower(str[i]);

结束输入

while(cin >> n)
while(cin >> n, n) 附加条件：n为正数，，等价于while(cin >> n && n)
while(cin >> a >> b, a, b)

以,作为分割符的读取

//absdf, efwf, csad
getline(cin, s1, ',');
getline(cin, s2, ',');
getline(cin, s3, ',');

约数

例如a能被b整除，a % b == 0，则b是a的约数，a也是a的约数

2>优化思路

钞票问题（653）

普通做法
定义多个变量用来存储每种钞票的数量，对数字不停地进行除和取余的操作
优化方法
利用循环

int money[8] = {100, 50, 20, 10, 5, 2, 1};   //先将所有面额存入数组money
int n; cin >> n;
for(int i = 0; i < 7; i++)
{cout << n / money[i] << "张" << i << "元" << endl;n % = money[i];
}

钞票和硬币问题（656）

不同点 面额又有整数又有小数，不能存到一个数组里面
解决方法 那就将小数都变成整数，所有数据*100

double n;
cin >> n;
int num = n * 100;
int money[15] = {10000, 5000, 2000, 1000, 500, 200, 100, 50, 25, 10, 5, 1};
for(int i = 0; i < 12; i++)
{printf("%d  %.2lf\n", num / money[i], money[i] * 1.0 / 100);num %= money[i];
}

动物（670）

对于每个字符串，不用单独提取某个字符用switch或if逐次进行判断
优化将它们拼接到一起，比较一个字符串即可

string a, fix;
for(int i = 0; i < 3; i++)
{cin >> a;if(i != 2) fix += a[0];else fix += a[2];   //因为第三列单词其中有两个首字母拼接相同，所以用第三个字母
}
if(fix == "var") cout << "aguia";
else if(fix == "vai") cout << "pomba";
//省略....

DDD(671)

常规解法 多个switch或者if依次判断
较短代码 将两类数据存入一个vector,按数字寻找再输出

#include <iostream>
#include <vector>using namespace std;
typedef pair<int, string> PII;  //存储数字和对应的城市名称
vector<PII> all = {{61, "Brasilia"}, {71, "Salvador"}, ....};  //后面省略，all是一个<int, string>类型的容器int main()
{int n;cin >> n;//在all中寻找n，for循环太慢，用二分查找int l = 0, r = all.size() - 1;while(l < r){int mid = l + r >> 1;if(all[mid].first >= n) r = mid;else l = mid + 1;}if(all[r].first != n) cout << "DDD nao cadastrado";  //判断n是否存在与all中else cout << all[l].second;
}

为什么这个二分查找不用先排序
因为我们并不是要返回下标；不排序也能进行查找，但是返回的是排好序之后的下标（虽然我们未进行排序操作）
要想知道排好序以前的下标该怎么办
初始就将下标和数字对应起来，可以放在一个二维数组，也可以放在一个<int, int>类型的vector容器中

余数（715）

普通方法
每个数都遍历一遍并判断余数是否为规定值
优化
跳过某些元素，直接输出正确的值

//要输出(1, 10000)所有除以n余2的数字
int n, ans = 2;
cin >> n;
while(ans < 10000)
{cout << ans << ' ';ans += n;
}

完全数（725）和质数（726）

以完全数为例分析

普通方法 <可能tle
时间复杂度为O(n * x)
优化方法
仔细想想：：一个数x，它的一个约数a一定<= sqrt(x),另一个约数b一定>= sqrt(x),用x / a就能得到b，所以我们只用遍历到sqrt(x)

int t; cin >> t;   //有t组数据
while(t--)
{int x, sum = 0; cin >> x;if(x == 1) cout << "no"; continue;for(int i = 1; i <= sqrt(x); i++){int j = x / i;if(x % i == 0)if(i != j) sum += i + j;else sum += i;   //若i和j相同，例如25 = 5 * 5，约数只有5，不能加两次}if(sum == x) cout << "yes" << endl;else cout << "no" << endl;
}

质数

#include <iostream>
#include <cmath>using namespace std;int main()
{int n; cin >> n;while(n--){int x;cin >> x;bool goal = true;for(int i = 2; i <= sqrt(x); i++){if(x % i == 0) {goal = false;break;}}if(goal || x == 2) cout << "yes" << endl;else cout << "no" << endl;}
}

菱形（727）

普通做法
有很多种做法，简单版找规律 / 复杂版找规律
优化
曼哈顿距离
d = abs (x1 - x2) + abs (y1 - y2)
输出n阶菱形，其实就是在n行n列的方格中寻找与中心点的曼哈顿距离<= n / 2 的格子

int n; cin >> n;
int sx = n / 2, sy = n / 2;
for(int i = 0; i < n; i++)
{for(int j = 0; j < n; j++){if(abs(sx - i) + abs(sy - j) <= n / 2) cout << '*'; //我是备注else cout << ' ';}cout << endl;
}

如何输出单层菱形
将上面有备注的一行中改成abs (sx - i) + abs (sy - j) == h ,h是你想要输出的特定的一层（就是曼哈顿距离=h的所有格子）

数组的右上部分（745）以及 746，747，748，749，750，751，752

普通做法
需要用到4个for循环，两个用来输入读取，两个用来判断计算
优化
只用两个for循环

745

寻找规律！ 设行为i，列为j，每一个绿色格子都满足 i < j

int sum = 0;
for(int i = 0; i < 12; i++)
{for(int j = 0; j < 12; j++){cin >> x;if(j > i) sum += x;}
}

747

找规律！ 每一个绿色格子都满足 i + j < 11
749

找规律！ 这张图的蓝色部分其实就是上面两张图重叠的部分
所以每一个绿色格子同时满足上面两个条件 i < j && i + j < 11

平方矩阵I（753）

法一：每一层的数字就是当前层每一边离最外层的最小距离

int n;
while(cin >> n, n)  //结束条件是k为0
{for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){cout << min(min(i, j), min(n - i + 1, n - j + 1)) << ' ';}cout << endl;}cout << endl;
}

法二：利用与中心点的最大距离

int n;
while(cin >> n, n)
{double x, y;if(n % 2) x = (n + 1) / 2.0, y = x;else x = (n + 1) / 2.0, y = x;for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){cout << (x - max(fabs(x - i), fabs(x - j))) << ' ';}cout << endl;}cout << endl;
}

法三：对角线翻折
亦可用于754
沿着对角线所有元素都对称，翻折后可以重叠
稍微复杂一点，要用数组存起来，再输出

int n;
while(cin >> n, n)
{int a[100][100] = {0};for(int i = 1; i <= n; i++){for(int j = i; j <= n - i + 1; j++){a[i][j] = a[j][i] = i;  //处理横着的元素再翻折a[n - i + 1][j] = a[j][n - i + 1] = i;  //处理竖着的元素再翻折}}for(int i = 1; i <= n; i++){for(int j = 1; j <= n; j++){cout << a[i][j] << ' ';}cout << endl;}cout << endl;
}

平方矩阵II（754）

num = abs(i - j) + 1;

平方矩阵III(755)

num = (int) pow(2, i + j);
或者
num = (1 << i) * (1 << j);

蛇形矩阵（756）

定义偏移量数组

int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};

int n, m, x = 0, y = 0, h, l, dr = 1;  //初始化向右
cin >> n >> m;
int a[101][101] = {0};
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
for(int i = 1; i <= n * m; i++)
{a[x][y] = i;h = x + dx[dr], l = dy + dy[dr];  //准备好下次的x, y再取判断是否成立if(h < 0 || l < 0 || h >= n || l >= m || a[h][l]){//不成立的原因：超出边界，重复dr = (dr + 1) % 4;h = x + dx[dr], l = y + dy[dr];}x = h, y = l;
}
for(int i = 0; i < n; i++)
{for(int j = 0; j < m; j++){cout << a[i][j] << ' ';}cout << endl;
}

信息加密（767）

普通
z变到a进行特判
优化
直接char put =（s[i] - 'a' + 1) % 26 + 'a';
或者char put = (s[i] - 'A' + 1) % 26 + 'A';

倒排单词（775）
法一：用字符串数组存储，再倒序输出

string s[100];
int i = 0;
while(cin >> s[i++]);
for(int j = i - 1; j >= 0; j--) cout << s[j] << ' ';

法二：叠加

string res, str;
while(cin >> str)
{res = str + ' ' + res;
}
cout << res;

字符串移位包含问题（776）

思路：既然一次移位，第一个字母就要移到最后一位，那么直接将该字符串复制粘贴，便能体现所有移位结果的相邻关系

string a, b;
cin >> a >> b;
a += a;
if(a.find(b) != std::string::npos) cout << "yes";
else cout << "no";

3>不知如何取名的一部分

斐波拉契数列的多直接问法与方法

输出第n项的值

输出前n项的值

递推

int n; cin >> n;
int a = 0, b = 1, c;
while(n--)
{c = a + b;a = b, b = c;cout << c << ' ';
}

递归

#include <iostream>using namespace std;int f(int n);
int main()
{int n; cin >> n;for(int i = 1; i <= n; i++) cout << f(i) << ' ';
}
int f(int n)
{if(n == 1) return 0;else if(n == 2) return 1;else return f(n - 1) + f(n - 2);}

输出前n项的和
在上面的代码中加上sum = 0, 依次sum += c 和 sum += f(i)

判断回文序列

法一：双指针

string a; cin >> a;
int l = 0, r = a.size() - 1;
bool goal = true;
while(l < r)
{if(a[l++] != a[r--]) {goal = false;break;}
}
if(goal) cout << "yes";
else cout << "no";

法二：reverse 函数

<algorithm>
string a; cin >> a;
string b = a;   //因为reverse是直接对a进行操作，所以要将a存到b中，方便之后比较
reverse(a.begin(), a.end());
if(a == b)  cout << "yes";
else cout << "no";

最小与最大重复单元

最小重复单元

法一

<algorithm>
string a; cin >> a;
for(int i = a.size(); i > 0; i--)  //以i作为重复次数
{if(a.size() % i == 0)  //说明i可以作为重复次数，能够整除，a.size() / i则是周期{int t = a.size() / i;string b;for(int j = 1; j <= i; j++) b += a.substr(0, t);if(a == b) cout << i << endl;}
}

法二

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/846960.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！