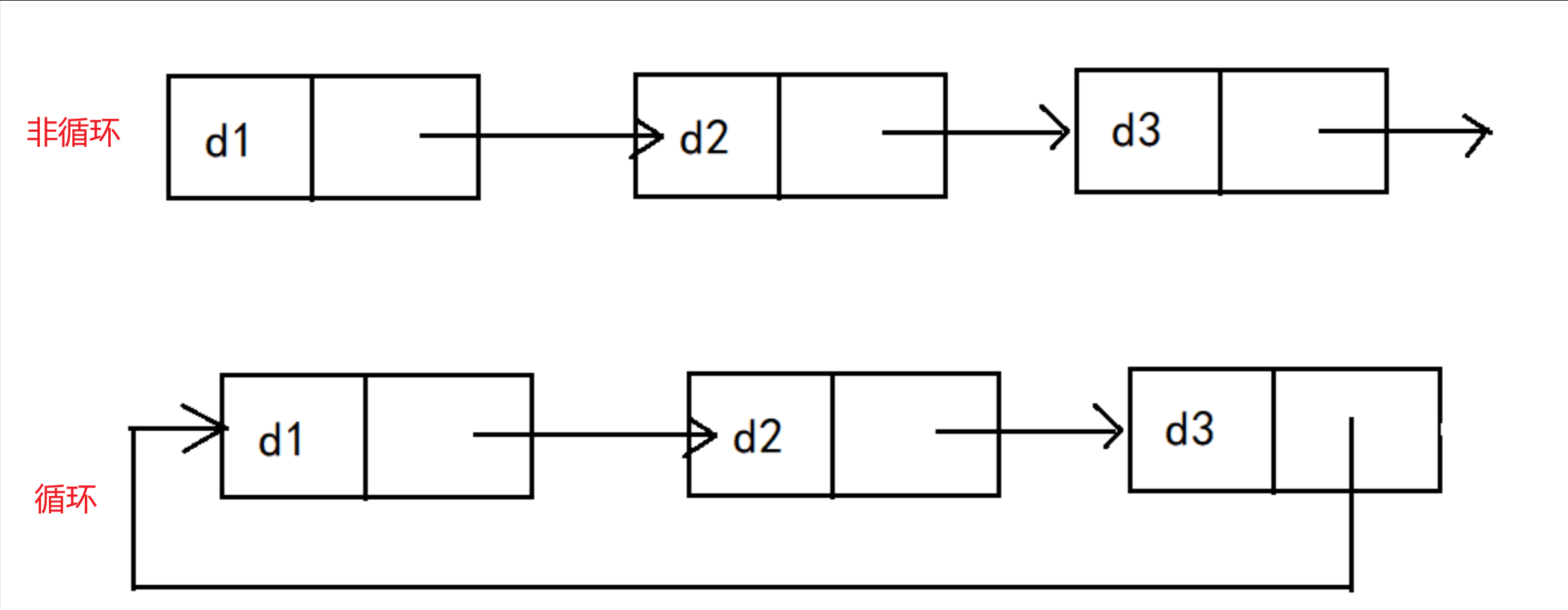
复数几何意义:https://zhuanlan.zhihu.com/p/646598747
https://zhuanlan.zhihu.com/p/359502624
Motivation & Abs
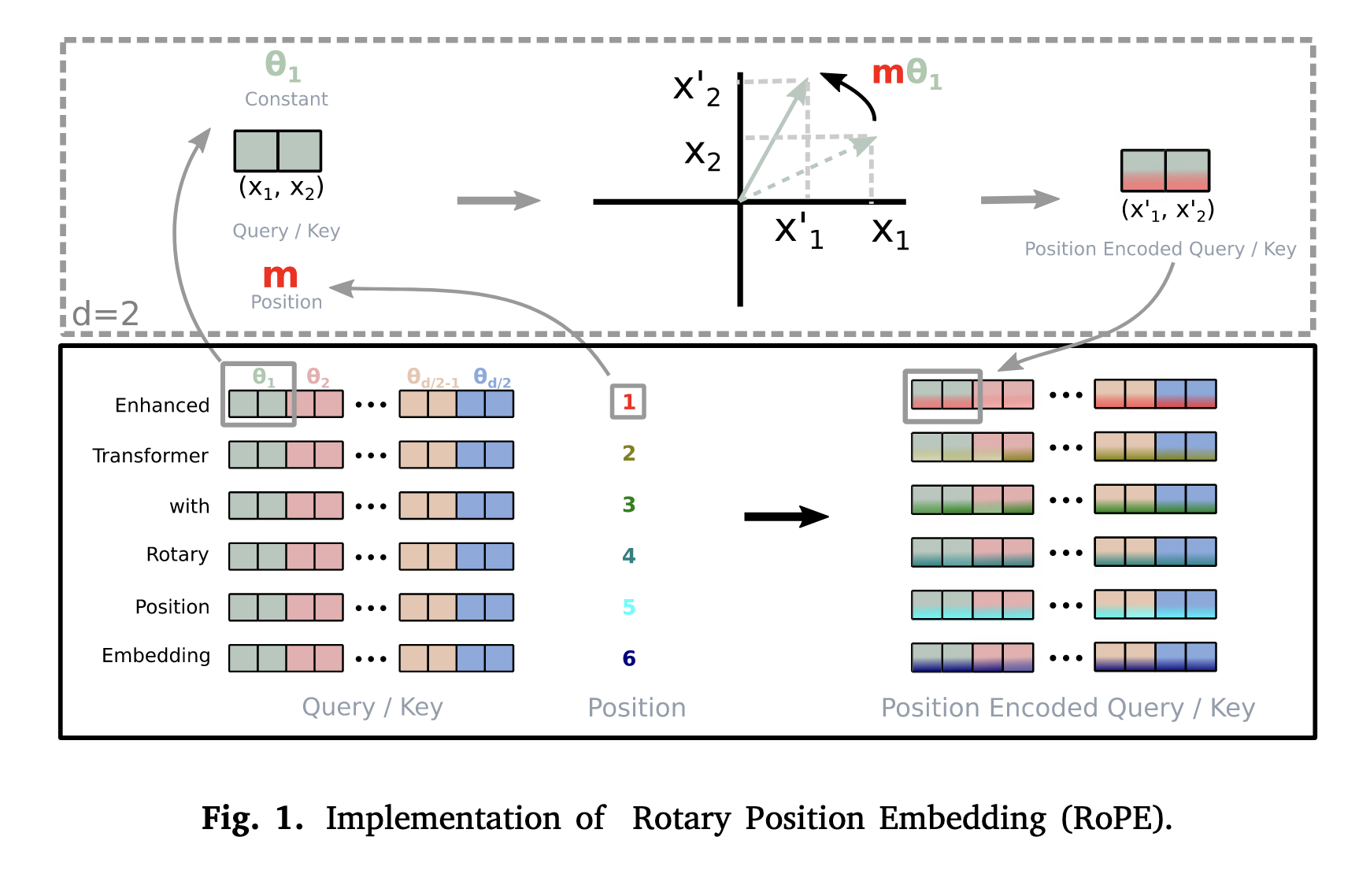
作者提出了旋转位置编码( Rotary Position Embedding, RoPE) 的新方法来有效利用位置信息。RoPE使用旋转矩阵对绝对位置进行编码,同时在自注意公式中纳入了明确的相对位置依赖性。RoPE 实现了序列长度的灵活性、随着相对距离的增加而衰减的标记间依赖性,以及为线性自注意力配备相对位置编码的能力。
Background
令\(\mathbb{S}_N=\{w_i\}_{i=1}^N\)为N个输入token构成的序列,对应的word embedding表示为\(\mathbb{E}_N=\{\textbf{x}_i\}_{i=1}^N\),其中\(\textbf{x}_i\in \mathbb{R}^d\)为d维的词嵌入,不包含任何的位置信息。自注意力首先将位置信息引入词嵌入,之后将其变为q、k、v:
\(\textbf{q}_m=f_q(\textbf{x}_m, m),\textbf{k}_n=f_k(\textbf{x}_n,n),\textbf{v}_n=f_v(\textbf{x}_n,n)\),其中\(\textbf{q}_m,\textbf{k}_n,\textbf{v}_n\)通过\(f\)函数引入了\(m\)和\(n\)的位置信息。
自注意力计算:
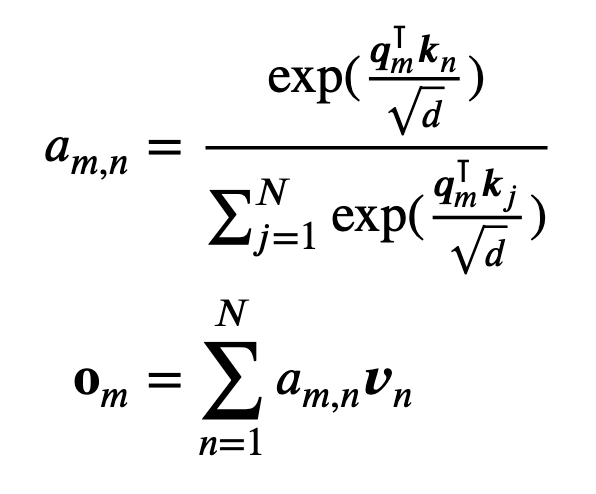
现有的基于transformer的位置编码方法旨在找到一个合适的函数\(f\)。
Method
Formulation
基于 Transformer 的语言建模通常通过自注意机制来利用单个标记的位置信息。\(\textbf{q}_m^{\top}\textbf{k}_n\)通常支持在不同位置的token之间进行信息的传递。想要引入相对位置信息,需要一个函数\(g\)计算\(\textbf{q}_m\)和\(\textbf{k}_n\)的内积,函数的输入为\(\textbf{x}_m\),\(\textbf{x}_n\)以及其相对位置\(m - n\):
\(⟨f_q(\textbf{x}_m,m),f_k(\textbf{x}_n,n⟩=g(\textbf{x}_m,\textbf{x}_n,m-n)\)
最终目标是找到一种等效的编码机制来求解\(f_q(\textbf{x}_m,m)\)以及\(f_k(\textbf{x}_n,n)\)以符合上述关系。
Rotary position embedding
作者首先分析了\(d=2\)时的一个简单例子。这种情况下,作者使用了向量在2D平面的几何性质以及其复数性质从而证明我们想要的解为:
其中\({\rm Re}[\cdot]\)为复数的实部,\((\textbf{W}_k\textbf{x}_k)^*\)为\((\textbf{W}_k\textbf{x}_k)\)的共轭复数,\(\theta\in \mathbb{R}\)为预设的非零常数。通过矩阵乘法表示:
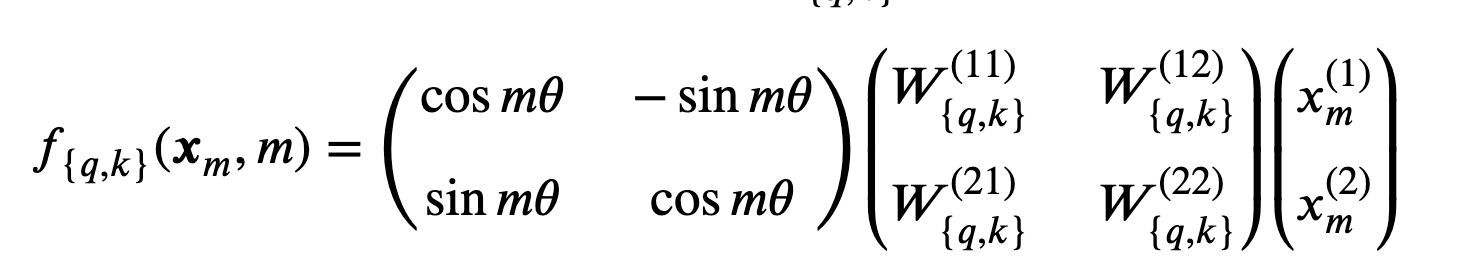
其中\((\textbf{x}_m^{(1)},x_m^{(2)})\)为2D平面的坐标。具体来说,其实就是将通过\(W\)变换后的embedding旋转其位置索引的角度倍数。
为了将上述算法扩展为更一般的形式(\(x_i\in\mathbb{R}^d\)且\(d\)为偶数),作者将\(d\)维空间分成了两个大小为\(d/2\)的子空间,利用内积的线性性对其进行组合:
\(f_{\{q,k\}}(\textbf{x}_m,m)=\textbf{R}^d_{\Theta,m}\textbf{W}_{\{q,k\}}\textbf{x}_m\),其中:
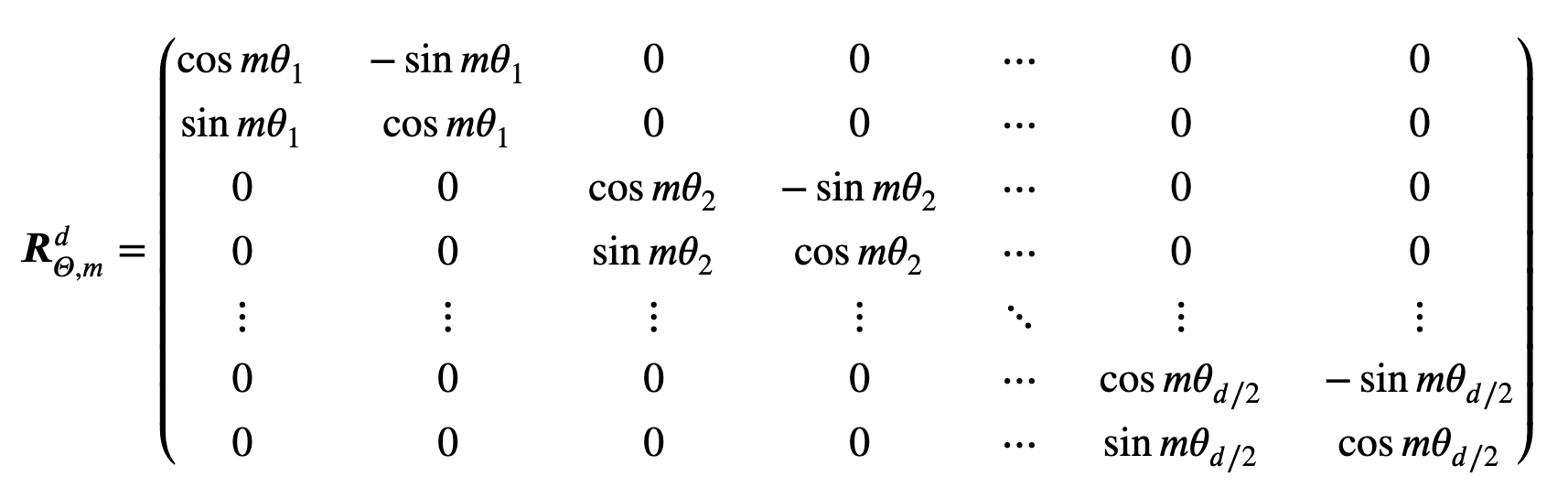
\(\textbf{R}^d_{\Theta,m}\)为旋转矩阵,\(\Theta=\{\theta_i=10000^{-2(i-1)/d},i\in [1,2,...,d/2]\}\)。
内积变为:
\(\textbf{q}_m^{\top} \textbf{k}_n=(\textbf{R}^d_{\Theta,m}\textbf{W}_q\textbf{x}_m)^{\top}(\textbf{R}^d_{\Theta,n}\textbf{W}_k \textbf{x}_n)=\textbf{x}^{\top}\textbf{W}_q\textbf{R}^d_{\Theta,n-m}\textbf{W}_k\textbf{x}_n\)
值得注意的是\(\textbf{R}_{\Theta}^d\)是一个正交矩阵,保证了编码位置信息过程中的稳定性(正交矩阵不会改变位置信息的相对关系?)。
Properties of RoPE
Long-term decay
\(\theta_i=10000^{-2i/d}\)可以保证睡着相对位置距离的增加,内积逐渐衰减。
RoPE with linear attention
自注意力可以用更一般的形式重写:
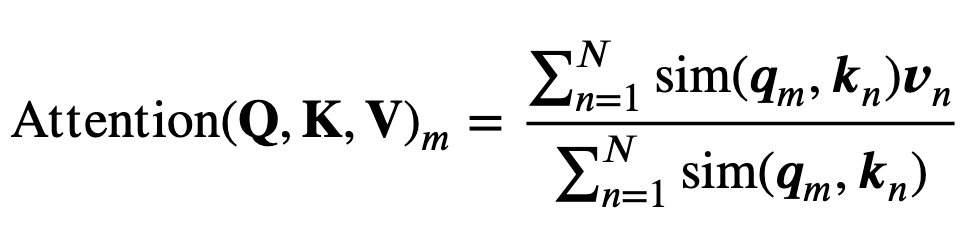
原始 self-attention 应该计算每对 token 的 query 和 key 的内积,引入了二次复杂度。线性注意力可以表示为:
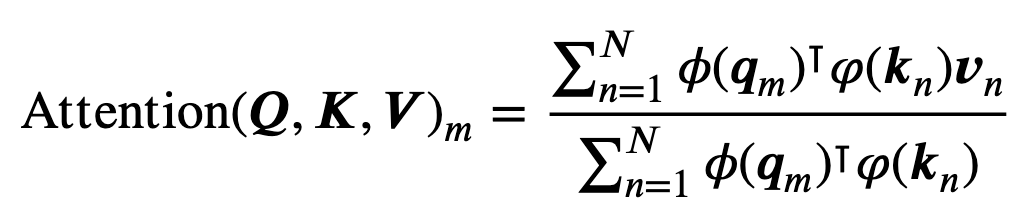
复杂度为\(O(n\times d^2)\)。引入RoPE:
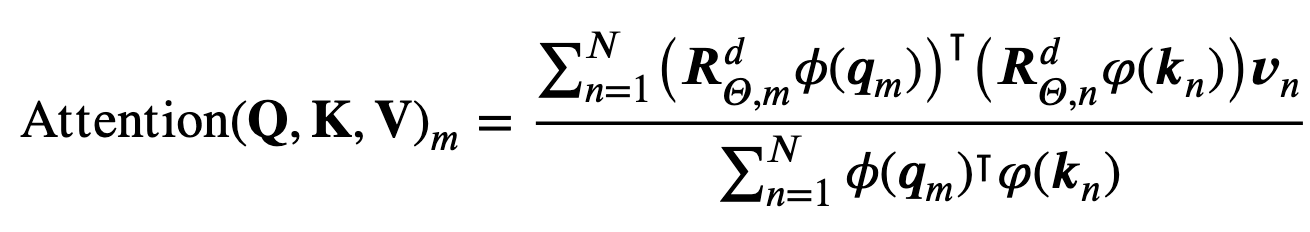
Computational efficient realization of rotary matrix multiplication
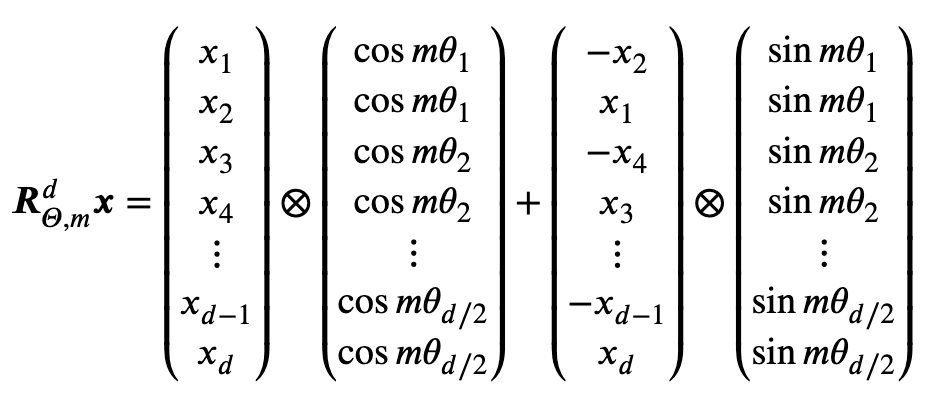
代码实现
TODO