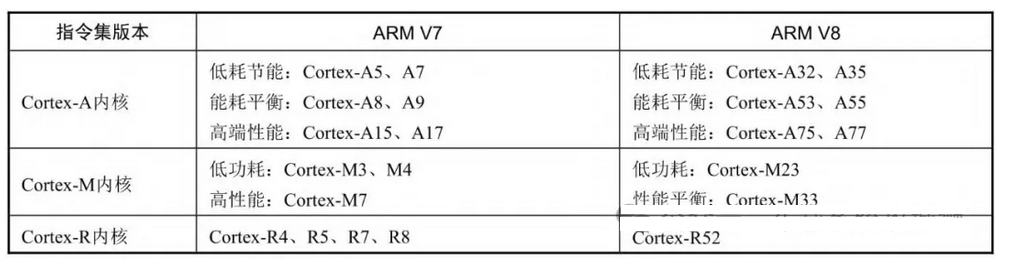
训练情况
赛后反思
C题开的时候太急了没求证直接猜了一个假结论,D题读错题了,死因:which can be one of the eight colors above or not.,可以变成八个颜色以外的(cao!),E题答案的下界取太小了(cao!)、F题二分求次数的时候,只能取正数
A题
判断字母是否重复出现,开一个变量记录即可。
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){string s; cin>>s;map<char,bool> v;bool flag = true;for(int i = 0;i<s.size();i++){if(v[s[i]]) flag = false;v[s[i]] = 1;}if(flag) cout<<"yes"<<endl;else cout<<"no"<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
B题
答案要最大,就是数列的极差
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;vector<int> a(n + 1);for(int i = 1;i<=n;i++) cin>>a[i];int ma = a[1],mi = a[1];for(int i = 2;i<=n;i++){ma = max(ma,a[i]);mi = min(mi,a[i]);}cout<<ma-mi<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
C题
先求和,如果不是 \(10\) 的倍数直接输出,如果是 \(10\) 的倍数,要答案尽可能大,那就从小到大减去一个数让和变成不是 \(10\) 的倍数,如果都不行答案就是 \(0\)。
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;vector<int> a(n + 1);int sum = 0;for(int i = 1;i<=n;i++) cin>>a[i],sum+=a[i];sort(a.begin() + 1,a.end());if(sum%10==0){for(int i = 1;i<=n;i++){if((sum-a[i])%10){cout<<sum-a[i]<<endl;return;}}cout<<0<<endl;} else cout<<sum<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
D题
分数段计数,我们发现分数段跨度都是 \(400\),所以我们直接除以 \(400\) 进行计数,如果 \(0 \sim 3199\) 都没有,那至少存在一个大于 \(3199\) 的,所以答案最小值至少为 \(1\),大于 \(3199\) 的可以变成任意颜色(坑点:可以变成八种颜色之外的),答案就是 \(0 \sim 3199\) 的人数 + 大于 \(3199\) 的人数。
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;vector<int> a(n + 1);for(int i = 1;i<=n;i++) cin>>a[i];vector<int> cnt(100,0);for(int i = 1;i<=n;i++) cnt[a[i]/400]++;int ans = 0;for(int i = 0;i<=7;i++) if(cnt[i]) ans++;if(ans == 0) cout<<1<<" ";else cout<<ans<<" ";for(int i = 8;i<=99;i++) ans += cnt[i];cout<<ans<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
E题
长度为 \(3n\) 的数列删掉 \(n\) 个,就是数列中选 \(2n\) 个,但是顺序不能够改变,然后选出来长度为 \(2n\) 的数列对半砍,我们发现可以去枚举那个对半砍的分界点,范围是 \(n \sim 2n\),为了让答案尽可能大,对于分界点左边的我们取尽可能大的 \(n\) 个,分界点右边的尽可能小的 \(n\) 个,这种动态维护排序后的最大和、与最小和,我们可以使用优先队列,求分界点左边最大的 \(n\) 个,和分界点右边最小的 \(n\) 个,求和我们可以预处理优先队列里的前后缀和,然后分界点移动的时候,最大值的优先队列去掉最小的,最小值的优先队列去掉最大的,对应的前后缀和也需要维护一下,最后答案就是 \(n \sim 2n\) 分界点左边最大值减右边最小值。
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;vector<int> a(3*n + 1);vector<int> pre(3*n + 3),suf(3*n+3);int ans = -LONG_LONG_MAX;for(int i = 1;i<=3*n;i++) cin>>a[i];priority_queue<int,vector<int>,greater<int>> mi;for(int i=1;i<=3*n;i++){mi.push(a[i]);pre[i]=pre[i-1]+a[i];while(mi.size()>n){pre[i]-=mi.top();mi.pop();}}priority_queue<int> ma;for(int i=3*n;i;i--){ma.push(a[i]);suf[i]=suf[i+1]+a[i];while(ma.size()>n){suf[i]-=ma.top();ma.pop();}}for(int i=n;i<=2*n;i++) ans=max(ans,pre[i]-suf[i+1]);cout<<ans<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
F题
我们可以看做范围AOE的伤害是保底的,选中的那个怪物会多 \(a-b\) 的伤害,我们根据答案可以计算出选中的次数,观察到二分单调性,考虑二分答案,选中的次数为 \(\sum_{i=1}^{n}{\lfloor \frac{t_i}{a-b} \rfloor(t_i-b \times mid>0)}\)。
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;const int N = 1e5 + 3;int n,a,b;
int h[N];
int t[N];bool pd(int x){for(int i = 1;i<=n;i++) t[i] = h[i];for(int i = 1;i<=n;i++) t[i] -= x*b;int ans = 0;for(int i = 1;i<=n;i++) if(t[i]>0) ans += ceil(1.0*t[i]/(a-b));return ans<=x;
}void solve(){cin>>n>>a>>b;int ma = 0;for(int i = 1;i<=n;i++) cin>>h[i],ma = max(ma,h[i]);int l = 1,r = ma,m;while(l<r){m = l + r >> 1;if(pd(m)) r = m;else l = m+1;}cout<<l<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}