其实线性回归不过就是在做两件事,画一条线并判断这条线到各个点的距离。
如下图:
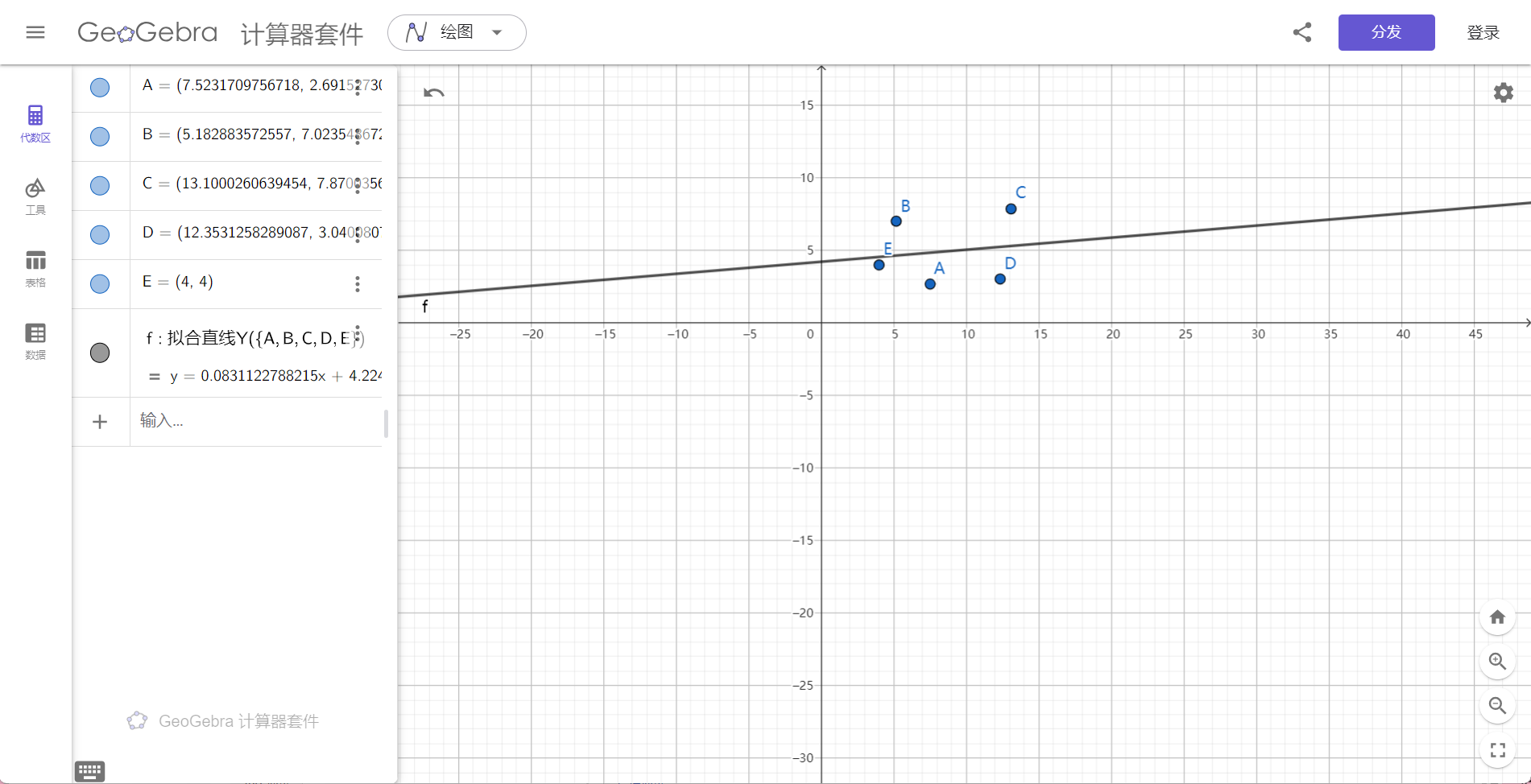
其中这条线便是距离各个点距离总和最小的直线。
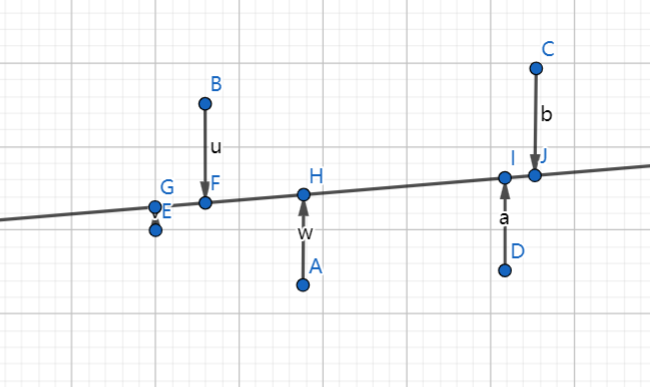
也就是e+u+w+b+a总和在直线为这个情况下最小。
但是什么时候这条线是我们需要的线呢?-- 线到各个点最短的时候便是。
我们先理解一下什么是凹函数: 凹函数即为在一定范围内,仅有一个最低点。并且不存在局部最低点。
我们的线性回归方程
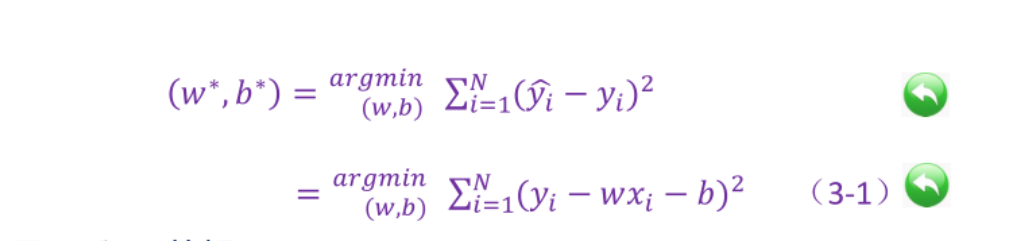
其中y^ i(x) - yi 是差值 进行累加。 最终结果最小的时候便是我们想要的结果。
我们改写为J(Θ) = (∑N i=0) (hi(x) - yi(x))^2;
其中我们应该知道h(x) = w0x+w1; 其实就是我们的简单二维直线方程;
接下来我们思考一个问题。是否随着直线 w0,和w1的变化 J(Θ)会随之增大减小?
很明显,是的。因为它是个凹函数:如下图

很好,我们接下来继续设计这个程序。
既然我们知道凹函数了,那我们只需要找到其中的最低点就好了。
那么很简单,我们对w0,w1求偏导即可。这里我们可以把函数改为J(Θ) =1/2 (∑N i=0) (hi(x) - yi(x))^2;方便我们求偏导
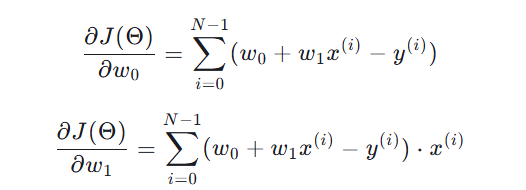
这个函数将为我们后来的梯度下降进行服务。
我们总结一下线性回归,其实就是取一条线,然后得到h(x)-y(x)的值进行累加,最后取h(x)为什么形式时候能得到最小值。