+++
date = '2024-12-21T10:12:41+08:00'
draft = true
title = '数值计算方法(1) 插值方法'
+++
初次发布于我的个人文档
之前有一期简单介绍了一下拉格朗日插值和数值积分微分方法,我感觉有点太简单了。所以这次打算开个系列,好好唠一唠。
什么是插值
在小学阶段,有一种题目叫找规律。
什么1,2,6,7,10要你填下一个数。但是经常去论坛逛的人会发现,网友啊总是会给一个惊为天人的答案,什么114514啊之类的。
然后抛出一个多项式,说你看这个114514啊是这个多项式在n=6的取值,前面的几个数也满足。所以这个找规律题下一个是114514。
事实上,这就是完成了一次数学上的插值任务。
他呢,相当于是已知若干点(在我前面的例子是已知(1,1),(2,2),(3,6),(4,7),(5,10),(6,114514))要找一个多项式恰好过这些点。
这就是一个插值问题。
当然,到了高中上了大学,你应该听说过导数这个玩意儿,所以有的时候我们还会要求多项式在某点的某阶导数是多少。
这也是插值问题。
我们也可以综合起来,既要求函数值又要求导数值,这样综合的插值问题我们也有办法解决。
我们先看最简单的,也是你们一定了解过的。
泰勒插值
看到名字不知道你想起泰勒公式了没有,没错泰勒插值就是泰勒多项式。
你可以回去翻翻泰勒公式的引入。
我给你看看百度百科是怎么介绍的。
在数学中,泰勒公式(英语:Taylor'sFormula)是一个用函数在某点的信息描述其附近取值的公式。这个公式来自于微积分的泰勒定理(Taylor's theorem),泰勒定理描述了一个可微函数,如果函数足够光滑的话,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值,这个多项式称为泰勒多项式(Taylor polynomial)。泰勒公式还给出了余项即这个多项式和实际的函数值之间的偏差。
你看哈,在已知函数在某一点的各阶导数值的情况之下,泰勒公式可以用这些导数值做系数构建一个多项式来近似函数在这一点的邻域中的值,这不就是插值问题吗?
也就是说,泰勒公式事实上是已知某一点的各阶导数,然后找了一个多项式,它的各阶导数值恰好是所给的导数值。
很显然,这就是我们前面说的给导数型的插值问题。其解就是泰勒多项式。
并且我们知道,泰勒多项式是唯一的。这个证明非常简单,并且我们可以进一步如果你要求到了函数的无穷阶导数恰好是f(x)的各阶导,那么我们知道,你得到的是泰勒级数,也就是函数f(x)的泰勒展开式。这里我们一并证明了。
我们假设,除了泰勒公式之外还有一个多项式(对级数的情况就是另一个幂级数)$$p(x)=\sum_{n=0}{+\infty}a_n(x-x_n)n$$ 它也满足要求,
对级数的情况,所谓的满足首先得满足p(x)收敛吧。所以还得要求p(x)在$$x_0$$附近内闭一致收敛于f(x)。
在这种情况下,不管是n有限的泰勒插值,还是n趋于无穷大的泰勒插值,最终的p(x)都可以逐项求导。
我们求n阶导看看,
$$p^{(n)}(x)=n!a_n+(n+1)n...3*2a_{n+1}(x-x_0)+...$$
再取$$x=x_0$$就有$$a_n=$$泰勒多项式对应项的系数,从而插值问题的泰勒多项式是唯一的,函数的泰勒展开式也是唯一的。
当然,泰勒展开不是本文关心的,我们只关心插值问题的泰勒多项式是唯一的。
既然如此,我们不禁要问,那已知n个点的函数值的插值问题其解是不是唯一的呢?
已知函数值的插值问题的唯一性
看标题就知道了,当然是唯一的。
我们假设$$p(x)=a_0+a_1x+a_2x+...+a_nx^n$$
这里有n+1个系数,所以我们需要给定n+1个不同的点,或者说n+1个点需要用n次插值多项式插值。
如果我们将这n+1个点代入就能得到
$a_0+a_1x_i+a_2x_i+...+a_nx_i^n=y_i$
显然,这是一个线性方程组,并且还有更令人兴奋的,
它的系数矩阵的行列式就是范德蒙德行列式。
从而,其系数矩阵的行列式是$x_i-x_j$的乘积,又由于这n+1个点是不同的,所以它的系数矩阵的行列式不为0。
那么根据克莱姆法则,这个线性方程组就有唯一解。
所以插值多项式是唯一的。
下一个问题自然就是怎么求解了。
拉格朗日插值
你是可以硬解刚刚的方程组啦,但是这有点痛苦。
拉格朗日插值的方法是,这样的:
你不是要求$$p(x_i)=y_i$$吗?
如果我能找到一系列多项式$$l_k(x)$$在$$x_k$$处取1,其他地方(指$$x_1,x_2,x_3,...,x_n$$但不包含$$x_k$$)取0,
那么p(x)不就是$$y_i l_k(x)$$$吗?
这就是拉格朗日插值法的思想。
其中$$l_k(x)$$被称为插值基函数。
那么我们怎么找到插值基函数呢?
其实很简单,$$l_k(x)$$在其他点取0从而其他点都是插值基函数的零点,所以插值基函数$$l_k(x)$$有因子
$$\prod_{i \neq k}(x-x_i)$$
那么我们怎么保证$$l_k(x)$$在$$x_k$$处取1呢?
很简单啊,把$$x_k$$代入刚刚的可能的因子,把代入的结果除掉不就行了?
也就是说$$l_k(x)=\frac{\prod_{i \neq k}(x-x_i)}{\prod_{i \neq k}(x_k-x_i)}$$
这就是拉格朗日插值基函数了。
则拉格朗日插值多项式就是
$$p(x)=\sum_{k=1}^n y_k l_k(x)$$
这就是拉格朗日插值公式了。
关于插值公式,这个插值公式呢他是一个多项式。
前面我们说过,n+1个节点要用n次多项式来插值,有时我们也说这样的插值是n次的。或者说,进行了n次插值。
特殊的,如果是一次插值和二次插值,有时我们会说成是线性插值和抛物插值。
接下来,如果我们把拉格朗日插值进一步优化,你就能得到埃特金插值。
埃特金插值
当然,这个埃特金插值说的优化但其实不是优化公式本身,而是给计算过程进行了优化。
前面我们说的拉格朗日插值有个很大的问题,就是他不具备承袭性。所谓承袭性也就是说我们已知n个点的插值多项式了,现在又加了一个点$$x_{n+1}$$,我们能在前面得到的插值多项式的基础上直接优化改进,直接以很小的计算量算出新的插值多项式。
埃特金插值源于这样的观察,首先我们要画一张这样的差值表
第一列是已知的点的横坐标,第二列是纵坐标。
我们在表的最上面一项和其他项之间进行线性插值,你会发现得到了第三列,也就是两个节点的线性插值。
如果在第三列的基础上再进行这样的线性插值得到的刚好是三个点的二次插值。
进一步地,如果在n次插值的基础上再进行线性插值就会得到n+1次插值多项式。
因此,想计算$$x_0,x_1,x_2,x_3$$的三次插值多项式,可以按表的方式计算到第五列。
如果接下来增加了$$x_4$$这个点,只需要计算表最下面一列就可以得到新的四次插值多项式了。
这就是埃特金插值,也称为埃特金逐次插值法。
牛顿插值
不过我更建议大家用牛顿插值。
因为牛顿插值在前面两种方法的基础上进一步优化,他也保证了承袭性,并且我们可以直接掏出一个公式。
牛顿插值源于对拉格朗日插值基函数的观察。
你看哈
$$l_0(x)=y_0$$
$$l_1(x)=y_0\frac{x-x_1}{x_0-x_1}+y_1\frac{x-x_0}{x_1-x_0}$$
有没有什么联系?
似乎很难看出来,但如果是这样的式子呢?
$$l_1(x)=y_0\frac{x-x_1}{x_0-x_1}+y_1\frac{x-x_0}{x_1-x_0}=y_0+\frac{y_1-y_0}{x_1-x_0}(x-x_0)$$
这下一眼就看出来了吧。
$$l_1(x)=l_0(x)+\frac{y_1-y_0}{x_1-x_0}(x-x_0)$$
更进一步地,可以发现
$$l_2(x)=l_1(x)+\frac{\frac{y_1-y_0}{x_1-x_0}-\frac{y_2-y_1}{x_2-x_1}}{x_2-x_0}(x-x_0)(x-x_1)$$
大佬这注意力真是恐怖如斯啊!!!
反正这个式子交给我我是不可能注意到的。
但是现在结论已经公之于众了,而且结论非常漂亮。
现在大家不难注意到,$$l_{n+1}(x)=l_n(x)+$$一个式子。
而这个式子有特征的,它的因子恰好是$$(x-x_0)(x-x_1)...(x-x_{n-1})$$
而前面那个分式,分母是$x_{n-1}-x_0$,分子是两个式子作差,而减式和被减式的结构还是这个式子原本的结构(递归了)。
前面那个分式就被我们称为差商。
我们现在递归定义差商,
参照百度百科的定义就是
不过我肯定是不能直接抛给你这玩意儿的,虽然很严谨没错,但是你很难看懂。
我们真正计算差商的方式是列差商计算表。
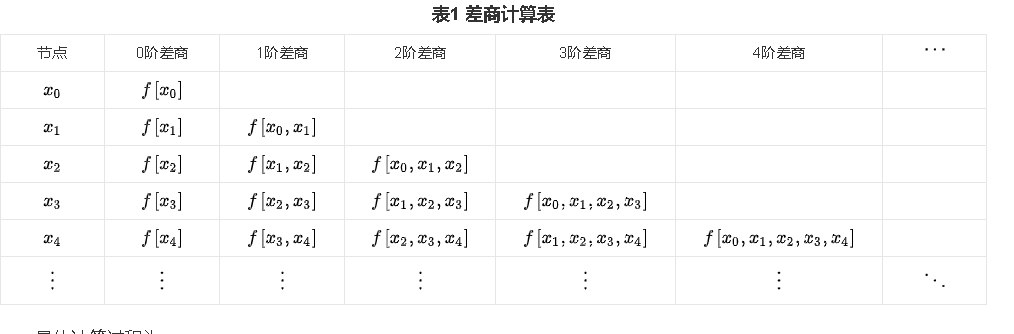
这个还是百度百科的图。
但是单看这个表你可能还是不容易理解,所以我又找了一张图。
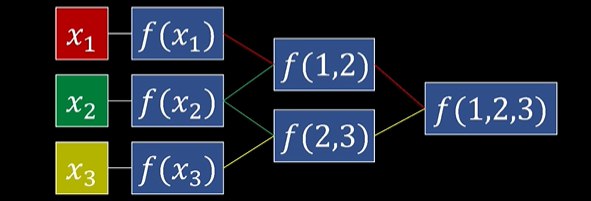
这张图来自B站UP主@泰勒猫爱丽丝的视频,BV号BV1du411a7qB。
这其实就是差商计算表但是他上了个色,现在就简洁好看多了。
第一列还是插值点的横坐标,第二列是纵坐标。
纵坐标其实就是对应点$$x_i$$的0阶差商$$f[x_i]$$。(归纳奠基)
接着相邻两项作差当1阶差商的分子。
我们用下一项-上一项,例如$$f[x_1,x_2]$$的分子就是$$f[x_2]-f[x_1]$$
那么分母呢?
你看泰勒猫爱丽丝上的色,你先找到我们在分子里说的下一项也就是$$f[x_2]$$,然后找到他的颜色绿色,再回到第一列找到绿色的点的横坐标$$x_2$$,这就是分母的前一项了,类似地你找到$$f[x_1]$$的颜色红色,再回到第一列找到红色点的横坐标$$x_1$$,作差$$x_2-x_1$$就是分母了。
所以$$f[x_1,x_2]=\frac{f[x_2]-f[x_1]}{x_2-x_1}$$
类似地,你会发现$$f[x_i,x_{i+1},...,x_j]=\frac{f[x_{i+1},x_{i+2},...,x_j]-f[x_i,x_{i+1},...,x_{j-1}]}{x_j-x_i}$$。
分母刚好就是左边[]记号内的两个端点的差。分子则是比他低一阶差商的差。并且你会发现,分子的前一项缺了$$x_i$$,后一项缺了$$x_j$$,这是直接从式子里看出差商规律的办法。
当然,自己手动计算的话我还是建议用刚刚说的那种上色+差商计算表的方法。
拉格朗日插值余项
现在我们有插值的计算公式了,但是很多时候插值做的其实是拟合的工作而不是前面说的找规律问题,那么我就要问了,我拟合的插值多项式和真实的f(x)的误差是多少,也就是要求余项$$R_n=f(x)-p_n(x)$$。
下面简单给个拉格朗日插值余项的结论,其定理的证明网上到处都是,我也没必要再赘述了。
关于拉格朗日插值的误差,有如下的拉格朗日插值余项定理,
设[a,b]上有插值节点$x_0,x_1,...,x_n$,f(x)在[a,b]上有连续的直到n+1阶导数,且希望$f(x_i)=y_i$,
那么就有当$x \in [a,b]$时,有
余项$R_n(x)=f(x)-p_n(x)=\frac{f{(n+1)}(\xi)}{(n+1)!}\prod_{k=0}n(x-x_k)$
其中$\xi \in [a,b]$
这就是拉格朗日插值的余项了。由于插值多项式是唯一的,所以其他的插值方法的余项也是这个。
聪明的你肯定越看越熟悉啊,这余项怎么感觉和泰勒公式的拉格朗日余项差不多?
其实还真有关系。我们现在探究的插值任务要么只有导数信息,要么只有函数值信息,如果二者混合呢?
艾尔米特插值
还有,你看那个差商的定义,你不觉得和导数是差不多的么?
现在如果我令插值点具有等间距h,并且令间距h趋于0,所谓的各阶差商就刚好是泰勒公式的系数了。
再次借用泰勒猫爱丽丝的视频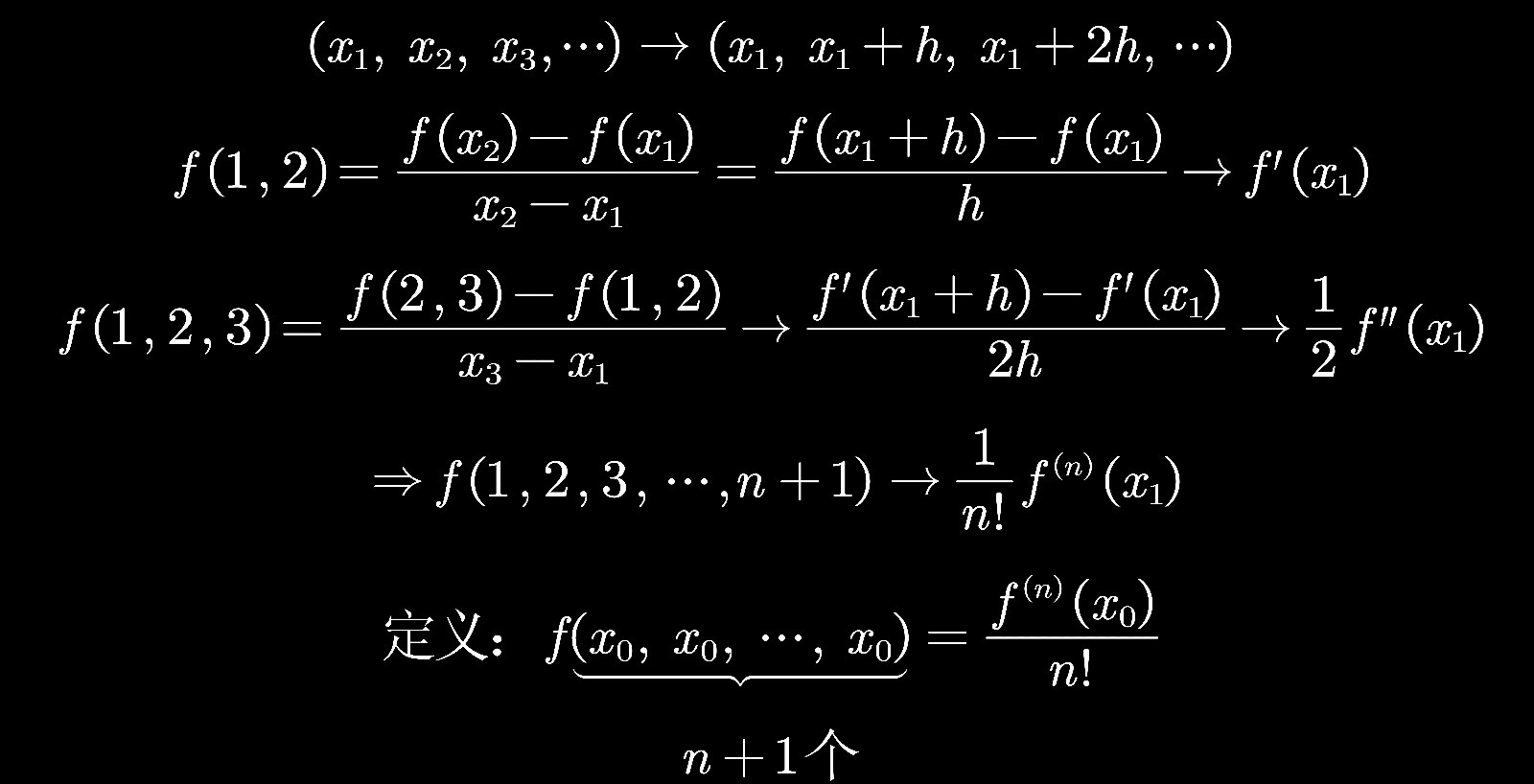
他的视频实在是太优秀了,希望大家都可以去观摩一下。
总之,我们按这样的情况推广牛顿插值就能得到兼容函数值信息和导数信息二者是艾尔米特插值方法了。
例如,已知$$x_0$$的函数值和一阶导数值,$$x_1$$的函数值。
那么就有
| 横坐标 | 零阶差商(函数值) | 一阶差商 | 二阶差商 |
|---|---|---|---|
| $$x_0$$ | $$f(x_0)$$ | ||
| $$x_0$$ | $$f(x_0)$$ | $$f'(x_0)$$ | |
| $$x_1$$ | $$f(x_1)$$ | $$\frac{f(x_0)-f(x_1)}{x_0-x_1}$$ | $$\frac{f'(x_0)-\frac{f(x_0)-f(x_1)}{x_0-x_1}}{x_0-x_1}$$ |
从而$$p(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f'(x_0)-\frac{f(x_0)-f(x_1)}{x_0-x_1}}{x_0-x_1}(x-x_0)(x-x_0)$$
你可以把式子化简一下,不过我这里化简了反而不利于观察出式子的来历,所以就不动了。
你可以验证一下,这个插值多项式就是满足$$x_0$$的函数值和一阶导数值,$$x_1$$的函数值的艾尔米特插值结果了。
误差的事后估计:回看埃特金插值
现在插值体系已经比较完备了,这里我想做的是其他的事,就是让你也看出埃特金插值。
额,牛顿插值你想直接看出来的话我也没有什么太好的办法,没法分享了。
我提供一个通过误差的事后估计看出埃特金插值的办法。
假定我们已知了3个节点$$x_0,x_1,x_2$$,在$$x_0,x_1$$和$$x_1,x_2$$之间进行一次线性插值,可以得到两个插值多项式。
例如,我们对$$f(x)=\sqrt{x}$$进行插值,取$$x_0=100,x_1=121,x_2=144$$,现在我们来求$$\sqrt{115}$$的近似值。
先用$$x_0,x_1$$进行线性插值得到$$\sqrt{115}\approx10.71428$$,然后再用$$x_1,x_2$$进行线性插值再把$$x'=115$$代入得到$$\sqrt{115}\approx10.68182$$。
接下来我们有办法用这两个近似值得到精度更高的近似值。
现在我们的情况是,通过两次线性插值得到了两个近似值$$y'_1,y'_2$$。
那么依据拉格朗日余项定理,有
$$f(x')-y'_1=\frac{f"(\alpha)}{2}(x'-x_0)(x'-x_1)$$
$$f(x')-y'_2=\frac{f"(\beta)}{2}(x'-x_1)(x'-x_2)$$
如果我们认为f的二阶导变化不大,也就是$$f''(\alpha)\approx f''(\beta)$$,然后两式相除就有,
$$\frac{f(x')-y'_1}{f(x')-y'_2}=\frac{x'-x_1}{x'-x_2}$$
把分子分母颠倒一下就是
$$\frac{f(x')-y'_2}{f(x')-y'_1}=\frac{x'-x_2}{x'-x_1}$$
再分离常数就有
$$1+\frac{y_1'-y_2'}{f(x')-y_1'}=1+\frac{x_1-x_2}{x'-x_1}$$
从而两边同时减去1,
$$\frac{y_1'-y_2'}{f(x')-y_1'}=\frac{x_1-x_2}{x'-x_1}$$
因此,
$$f(x')-y_1'=\frac{x'-x_1}{x_2-x_1}(y_2'-y_1')$$
也就是说,我们估计出了一个准确的误差$$f(x')-y_1'\approx\frac{x'-x_1}{x_2-x_1}(y_2'-y_1')$$
这样的话,我已经知道估计出准确值和近似值的误差了,我再把误差补回去不就是一个更精确的近似值了?
所以我们可以得到更精确的近似值为$$y_1'+\frac{x'-x_1}{x_2-x_1}(y_2'-y_1')$$,对本例就是10.7228。
你会发现,这个近似值就是抛物插值的结果,这就是误差的事后估计法。
也就是说,我们通过误差的事后估计法可以使得插值的次数+1,这不就也是埃特金插值?
龙格现象和过拟合
现在你可能有一个大概的印象,就是说插值点越多,插值次数越高精度越高。
但其实并不是这样的。在机器学习领域有一个叫过拟合的词,说的是你啊用这种方式拼命堆数据大力出奇迹,结果反而会变差。
例如,你搞了一个分辨叶子的模型,然后给他喂了一万张叶子图片,结果里面的叶子都是带锯齿的,所以模型学习到了带锯齿的东西是叶子,从而你给他一个没锯齿的叶子他会判否,给他个有锯齿的其他东西他却说是叶子。
我们插值也有类似的过拟合现象。
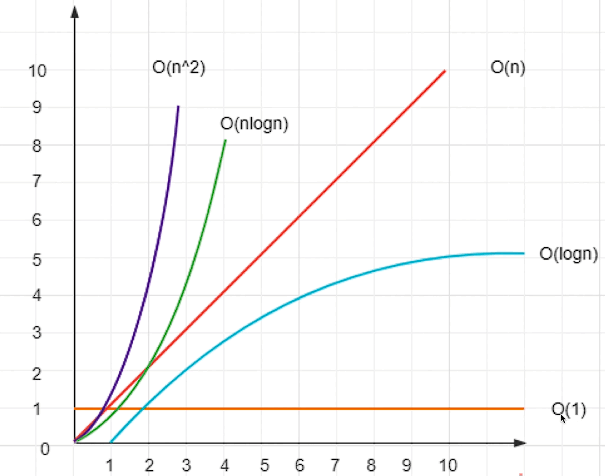
插值点越多,插值次数越高,插值多项式的次数也越高,而$$x^100$$次方,你x稍微变一下,y就会差很多,从而会导致你的插值多项式在端点处震荡地非常离谱,导致精度反而下降了。这就是龙格现象,我个人觉得也是一种过拟合。
参考百度百科的图,
你会看到,高次插值多项式在两个端点处疯狂震荡,这样反而会导致精度下降。
分段低次插值
那么怎么解决这个问题呢?答案是用多次低次插值来拟合函数。
你给了我1,2,3,4,5,6,7,8,9,10这10个点的信息,我怎么做呢?
我拼一个分段函数给你,x在[i,i+1]的时候,表达式就是i和i+1的线性插值。
当然,也可以是x在[i-1,i+1]的时候,表达式是i-1,i,i+1的二次插值等等。
总之就是给你这样的分段函数,并且他们的插值次数都不高。
这就是分段低次插值。
但是这样的插值还是有问题,他在分界点往往不可导,这是我们不希望看到的。
样条插值
所以样条插值应运而生。
其实理论说起来也比较简单。
例如还是已知1,2,3,4,5,6,7,8,9,10的信息。
我把他分成[1,2],[2,3],...,[9,10]这样的9段。
每一段我都用一个三次函数拟合(这个函数被称为样条函数,这样的样条插值被称为三次样条插值,当然你也可以通过改变段的分法来改变样条函数的次数)。
在这里每一段只有两个点,按道理线性插值就足以了啊,为什么要用三次函数呢?
这是因为我要强行加条件了,我要求这个样条函数在分界点连续,即2,3,4,5,6,7,8,9处函数值相等。
这是附加了8个条件。
而原本有9个三次函数,每个三次函数有4个系数,也就是需要36个条件。
现在只用了8个,还绰绰有余呢。
现在我再加强条件,要求样条函数在分界点一阶可导,即要求分界点左右导数相等,这又是8个条件。
进一步,我还要求二阶可导,又是8个条件。
这才用了24个条件。还剩下12个条件。
当然,我自然是需要要求函数在1到10每个点上函数值等于所给的需要插值的函数值的,所以还有2个条件。
这两个条件给1和10这两个最后的边界点,可以是规定边界点的一阶导或者二阶导都可以,反正把这两个条件用了就可以了。
然后用计算机来求解就ok了。
额,你不会觉得36元一次方程组我要手算吧,不会吧不会吧。
真的有那个毅力手算的朋友,告诉你一下,最后的线性方程组是一个三对角方程组,后面我会介绍追赶法求解三对角方程组的方法的,这种方程最好用那个方法解。