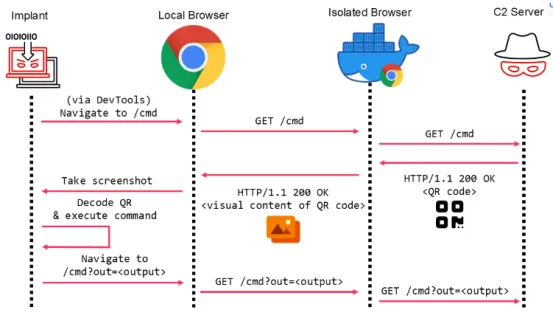
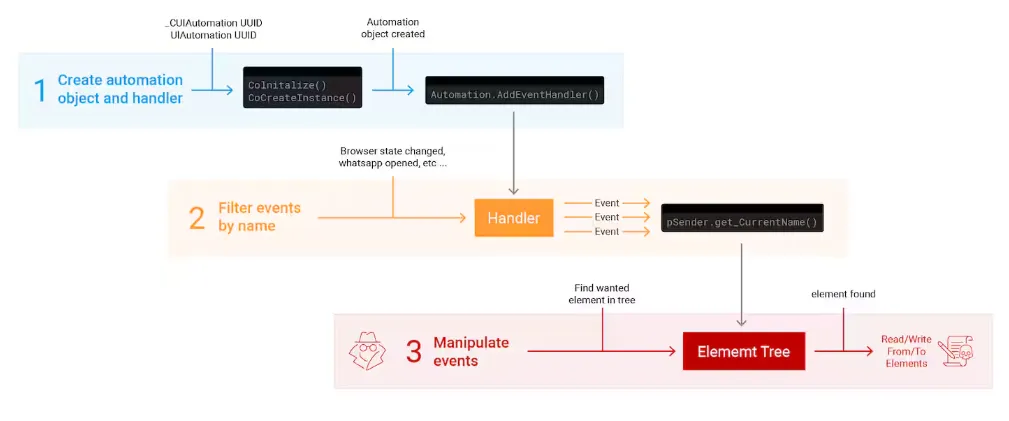
总体而言还算是比较简单的一场模拟赛(但我是废物,被小孩哥直接拉爆了)。
T1 坦克
Describe
众所周知,甜所妹妹很可爱。 甜所妹妹有 \(n\) 辆相同的坦克,你有 \(m\) 辆相同的坦克,但你们两人的坦克是不同的。甜所妹妹的坦克打爆你的一辆坦克需要 \(a\) 炮,你的坦克打爆甜所妹妹的一辆坦克需要 \(b\) 炮。
甜所妹妹和你在一个空旷的地图上对战,每个回合每辆坦克可以打出 1 炮。甜所妹妹和你的坦克都会同时以最优策略。每个回合中,首先甜所妹妹和你都会向自己的每一辆坦克分别下达命令,确定该坦克本回合攻击对方的哪一辆坦克;然后双方所有坦克同时开炮,所有炮弹的飞行时间都相同,即本回合被命中的坦克都是同时被命中的。如果某辆坦克被打爆了,那么它在以后的回合中将无法再进行攻击。你们会一直让坦克互相开炮,直到某一方所有坦克被全部打爆为止。
甜所妹妹想知道把你的坦克打光后,自己还剩多少坦克。如果她打不过你,输出 " 0 "(不含引号) 。你和甜所妹妹玩了 \(T\) 轮游戏,也就是说本题有 \(T\) 组测试数据。
Input
第一行输入一个正整数 \(T\) ,表示数据组数。 对于每一组测试数据,一共输入一行四个正整数,分别为 \(n,m,a,b\),表示双方的坦克数量和每辆坦克的生命值。
输入样例:
5
10 2 15 1
2 1 2 1
2 1 3 1
10 8 4 4
10 8 1145141919 1145141919
Output
对于每一组数据,输出一个非负整数,表示答案。
输出样例:
3
1
0
5
6
Solution
首先,两方最优解肯定都是优先集火对方血量最低的坦克。
由于要记录坦克数量和某一个的血量太过复杂,所以我们选择记录两方的总血量。然后通过总血量整出,取模等操作,计算可以对对方造成的伤害。
然后可以写为优化一下,就是一次打多轮。因为一方的单个血量可能太大,一轮一轮太慢了,所以我们可以一次打多轮,直接把这个残血的打掉。
Code
#include<bits/stdc++.h>
#define int long long
using namespace std;
int T,n,m,a,b;
void work(){cin>>n>>m>>a>>b;if(m>=n&&a>=b){cout<<"0\n";return;}int x=m*a,y=n*b;while(x>0&&y>0){n=ceil(y*1.0/b),m=ceil(x*1.0/a);int t=max(min(ceil((x%a)*1.0/n),ceil((y%b)*1.0/m)),1.0);x-=n*t;y-=m*t;}cout<<max(0ll,(y+b-1)/b)<<"\n";
}
signed main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);cin>>T;while(T--)work();return 0;
}
T2 火柴棍
Describe
你有 \(n\) 个火柴棍,问用完所有的火柴棍可以摆出的最小的数(不含前导零,但可以为 0 )是多少?
由于你能摆出的数字可能非常大,请输出对 998244853 取模的结果。
提示:0~9 所使用的火柴棍数量分别为:6,2,5,5,4,5,6,3,7,6
Input
第一行一个整数 \(T\) 表示数据组数。
对于每组数据输入一行一个整数 \(n\) 。
输入样例:
2
7
8
Output
对于每组数据输出一行一个整数,表示答案。
输出样例:
8
10
Solution
首先我们考虑,想要让一个数最小,首先要让它的位数最小,所以我们选择先将所有的位置都填上 \(8\)(因为 \(8\) 所需的火柴棍最多),然后在根据剩下的火柴棍数量安排最开始那几位的数字即可。
但是他要让我们对 998244853 取模,一位一位边加数字边取模太慢了。我们想到后面的很多位都是 8,相当于 \((8\times 11···1)\mod 998244853\),前面只有几位是别的数字,相当于 \((x\times 10^n)\mod 998244853\),所以我们考虑将 \(11···1\mod 998244853\) 和 \(10^n\mod 998244853\) 都预处理出来,最后统一乘上即可。
Code
#include<bits/stdc++.h>
#define int long long
#define N 15005
#define mod 998244853
using namespace std;
int T,n,a[N],b[N];
signed main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);b[0]=1;for(int i=1;i<=15000;i++)a[i]=(a[i-1]*10+1)%mod,b[i]=b[i-1]*10%mod;cin>>T;while(T--){cin>>n;if(n<7){if(n==2)cout<<"1\n";if(n==5)cout<<"2\n";if(n==4)cout<<"4\n";if(n==6)cout<<"0\n";if(n==3)cout<<"7\n";continue;}int num=n/7,sum=n%7,x=0;if(sum==1)--num,x=10;if(sum==2)x=1;if(sum==3){if(num>1)num-=2,x=200;else --num,x=22;}if(sum==4)--num,x=20;if(sum==5)x=2;if(sum==6)x=6;cout<<(x*b[num]%mod+8*a[num]%mod)%mod<<"\n";}return 0;
}
T3 子集计数
Describe
给定一个长度为 \(n\) 的非负整数序列 \((a_1,a_2,⋯,a_n)\),对每个 \(i\in [1,n]\) 求有多少个子序列 \((a_{j_1},a_{j_2},⋯,a_{j_k})\),满足 \(k≥1,1≤j_1<j_2<⋯<j_k=i\),且将序列中的数视为二进制表示的集合后 \(a_{j_1}\subseteq a_{j_2}\subseteq ⋯\subseteq a_{j_k}\),答案对 \(998244353\) 取模。
Input
第一行一个整数 \(n\)。
接下来 \(n\) 行,每行一个非负整数,依次是 \(a_1,a_2,⋯,a_n\)。
输入样例:
5
1
2
3
4
5
Output
输出 \(n\) 行,每行 \(1\) 个整数,依次是 \(i=1,2,⋯,n\) 的答案\(\mod 998244353\) 后的结果。
输出样例;
1
1
3
1
3
Solution
20pts
\(O(n^2)\) 暴力 DP 即可。
设 \(f_i\) 表示以 \(a_i\) 结尾的序列数量,若 \(j<i\) 且 \(a_j\subseteq a_i\),则 \(f_j\to f_i\),初始值全部为 \(1\)。
有个小技巧是 \(x\vee y=x\) 与 \(y\subseteq x\) 是等价的。
#include<bits/stdc++.h>
#define mod 998244353
#define N 100005
using namespace std;
int n,a[N],dp[N];
int main(){cin>>n;for(int i=1;i<=n;i++)cin>>a[i];for(int i=1;i<=n;i++){dp[i]=1;for(int j=1;j<i;j++)if((a[i]|a[j])==a[i])(dp[i]+=dp[j])%=mod;cout<<dp[i]<<"\n";}return 0;
}
30pts
法1:
设 \(g_s\) 是所有 \(a_j=s\) 的 \(f_s\) 之和,转移时枚举 \(s\subseteq a_i\),\(g_s\to f_i\),转以后 \(f_i\to g_{a_i}\)。
#include<bits/stdc++.h>
#define int long long
#define N 100005
#define mod 998244353
using namespace std;
int n,x,a[N],dp[N],g[N];
signed main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n;i++){cin>>a[i];dp[i]=1;for(int j=0;j<=a[i];j++){if((j|a[i])==a[i])(dp[i]+=g[j])%=mod;}(g[a[i]]+=dp[i])%=mod;cout<<dp[i]<<"\n";}return 0;
}
法2:
设 \(g_s\) 是所有 \(a_j\subseteq s\) 的 \(f_j\) 之和,转移时 \(g_{a_j}\to f_i\),转以后枚举 \(s\) 满足 \(a_i\subseteq s\),\(f_i\to g_s\)
#include<bits/stdc++.h>
#define int long long
#define N 100005
#define mod 998244353
using namespace std;
int n,x,a[N],dp[N],g[N],mx;
signed main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n;i++)cin>>a[i],mx=max(mx,a[i]);for(int i=1;i<=n;i++){(dp[i]=g[a[i]]+1)%=mod;cout<<dp[i]<<"\n";for(int j=a[i];j<=mx;j++){if((a[i]|j)==j)(g[j]+=dp[i])%=mod;}}return 0;
}
时间复杂度都为 \(O(2^m))\),\(m\) 表示 \(\max(\log a_i))\)
100pts
将 30pts 的两种做法结合一下,将 \(m\le 16\) 拆分成低8位和高8位。低8位采用法1,高8位采用法2。
设 \(g_{s,t}\) 表示 \(a_i>>8\subseteq s\) 且 \(a_i\wedge 255=t\) 的所有 \(f_i\) 之和。
转移时枚举 \(t\subseteq a_i\wedge 255\),令 \(s=a_i>>8\),\(g_{s,t}\to f_i\)。
转移后枚举 \(s\) 满足 \(a_i>>8\subseteq s\),令 \(t=a_i\wedge 255\),\(f_i\to g_{s,t}\)
(这种高 \(m/2\) 位和低 \(m/2\) 位的小技巧值得记录一下)
#include<bits/stdc++.h>
#define int long long
#define N 100005
#define mod 998244353
using namespace std;
int n,x,a[N],dp[N],g[300][300],mx;
signed main(){ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n;i++){cin>>a[i],mx=max(mx,(a[i]>>8));}for(int i=1;i<=n;i++){dp[i]=1;int x=a[i]&255,y=a[i]>>8;for(int j=0;j<=x;j++){if((j|x)==x)(dp[i]+=g[y][j])%=mod;}cout<<dp[i]<<"\n";for(int j=y;j<=mx;j++){if((j|y)==j)(g[j][x]+=dp[i])%=mod;}}return 0;
}
T4 排列
Describe
对于序列长度为 \(n\) 的自然数序列 \({a}\),若序列中的每个数都为 \(1\) 到 \(n\) 的自然数且互不相同,则称序列 \({a}\) 为好的序列。
给定自然数 \(n\),我们称所有长度为 \(n\) 的好的序列 \((p1,p2,…,pn)\) 中满足序列中任意相邻两数以及尾首两数产生的 \(n\) 对有序二元对中,前面的数字模后面的数字的结果不超过 \(2\),为完美的序列。
现在需要你统计所有长度为 \(n\) 的好的序列中,有多少个是完美的序列。
输出满足条件的序列个数对 \(10^9+7\) 取模的结果。
Input
一行一个整数 \(n\) 代表序列的长度。
输入样例:
4
Output
一行一个整数代表完美的序列的数量。
输出样例:
16
Solution
打表可以发现(也不一定必须要),将任意一条完美的序列首尾相连后再重新断开,一定会有一种是两个递减的序列(当然序列可以为空)拼在一起,而且它们的最后一个一定是 \(1\) 或 \(2\)。
因为在 \(x\) 在 \(y\) 前面的情况下,\(x<y\),那么 \(x\) 就必须要小于等于 \(2\),这样才能保证取模符合要求。也就是说,只有 \(1\) 和 \(2\) 才能在比它们大的数的前面,其他必须是递减。
所以题目也就被转化成从前往后依次把数放进前后两个集合中,集合内部的顺序不用管,一定是递减;两个集合的前后顺序也不用管,因为谁前谁后都可以,只不过是断环的位置不同。
最后统计答案的时候,要将这个方案数乘 \(n\),因为我们只管了前后两个集合,把他们拼在一起一共会有 \(n\) 种断环的方式。
我们设 \(dp_{i,j}\) 表示的是后面的集合已经选到了 \(i\)(其实也就是最大值为 \(i\)),前面的集合选到了 \(j\)。保证 \(i>j\),且 \(1~n\) 都选完了。
dp转移:
- \(dp_{i,j}\to dp_{i+1,j}\) 这个必然满足,因为 \(i+1\mod i=1\)
- \(dp_{i,j}\to dp_{i+1,i}(满足 i+1\mod j\le 2)\) 这个有些难以理解。可以认为是将 \(i+1\) 加到了前面,因为要保证 \(i>j\),所以将前后两个集合顺序调换了一下。
复杂度 \(O(n^2)\)
因为所有 \(dp_i\) 都只与 \(dp_{i-1}\) 有关,所以可以将第一维滚掉。
这样第一种转移就可以不管了。再看第二种转移,要求 \(i+1\mod j\le 2\),所以一共有三种状态,取模后等于 \(-1\)(就是 \(2\)),等于 \(0\),等于 \(1\),也就是 \(j\) 整除 \(i-1\),\(i\),或 \(i+1\),便利的时候从这三个开始,每次加 \(j\)。
Code
#include<bits/stdc++.h>
#define int long long
#define N 1000005
#define mod 1000000007
using namespace std;
int n,dp[N],ans;
signed main() {cin>>n;dp[1]=1;for(int j=1;j<n;j++){if(j<=2){for(int i=j+1;i<n;i++)(dp[i]+=dp[j])%=mod;}else{for(int k=-1;k<=1;k++){for(int i=j+k;i<n;i+=j){if(j<i)(dp[i]+=dp[j])%=mod;}}}}for(int i=1;i<n;i++){(ans+=dp[i])%=mod;}cout<<ans*n%mod;return 0;
}