[CF2057F] Formation 做题记录

link

对我比较有意义的一道题目。

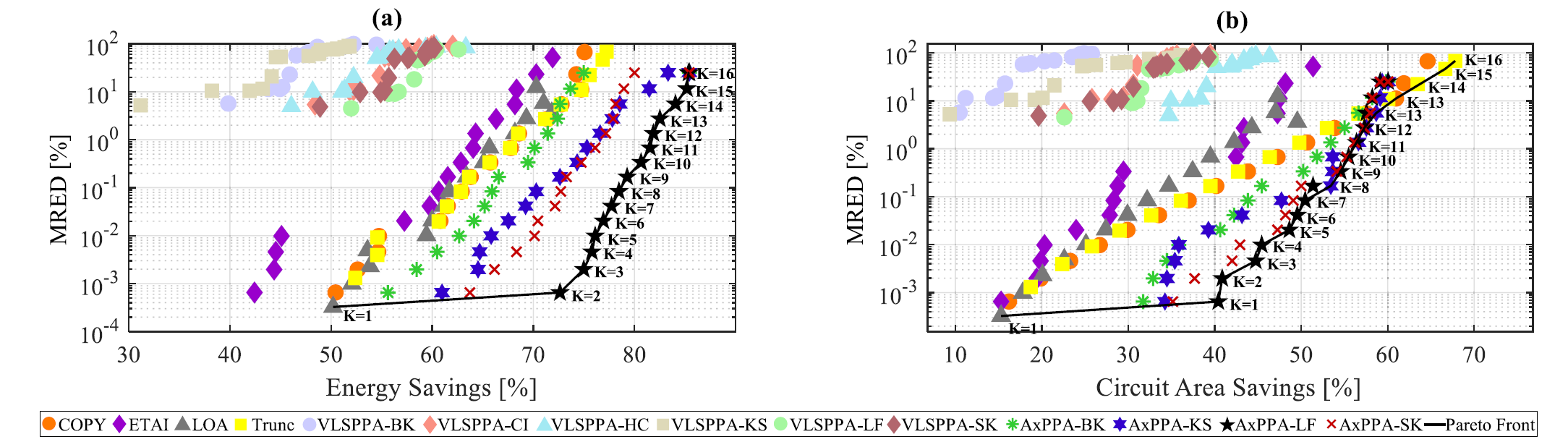
我们先逐步分析，对于单个询问，先钦定最大值位置 \(i\)，我们现在的目标是最大化 \(a_i\) 的值。

这显然有单调性，考虑二分一个 \(mid\) 表示最终值，那么会出现一个 \(l(l\le i)\) 以及一个序列 \(c_{0\dots l - 1}\) 有 \(c_i = \lceil \dfrac {mid} {2^i}\rceil\)：

• \(\forall j \in [0, l - 1], \ a_{i - j} \le c_j\)

• \(l = i\) 或 \(a_{i - l} \ge c_j\)

• 代价为 \(\sum\limits_{j = 0} ^ {l - 1} (c_j - a_{i - j})\)

注意到若固定一个 \(l\)，\(mid\) 的合法取值形如一个区间。此时把代价式子拆开 \(\sum\limits_{j = 0} ^ {l - 1} c_j - \sum\limits_{j = 0} ^ {l - 1} a_{i - j}\)，只分别和 \(mid\) 与 \(i\) 有关。

固定 \(l\)，枚举 \(i\)，我们会得到若干个三元组 \((l, r, w)\)，表示一个 \(mid\) 取值区间以及其代价常数（即是 \(\sum\limits_{j = 0} ^ {l - 1} a_{i - j}\)）。这 \(n\) 个区间将数轴分成了若干段，每段求出覆盖它的区间的最大代价常数。这样，每次询问一个 \(mid\)，只需要二分出 \(mid\) 在哪一段即可。

这样即可 \(\mathcal O(\log ^ 2 V \log n)\) 求出一个询问的答案。

考虑 \(q\) 个询问，尝试优化到 \(2\log\)。发现唯一能优化的点在于二分查找 \(mid\) 所属哪一段，考虑将所有询问一起二分，将所有 \(mid\) 和这 \(\mathcal O(n)\) 段一起双指针，时间复杂度 \(\mathcal O(q\log ^ 2 V)\)。

• 启示：这题先二分，从枚举 \(i\) 转为枚举 \(l\)，说明暴力是通往正解的必要途径，也体现了转置思想的重要性（更换枚举对象）。然后固定 \(l\)，处理出 \(\mathcal O(n)\) 段，这一步我根本没有想到，原因在于我只从常规的数据结构以及其他知识结构出发，忽略了整理信息这一方向。最后是类似整体二分的 trick。

点击查看代码

#include <bits/stdc++.h>namespace Initial {#define ll long long#define ull unsigned long long#define fi first#define se second#define mkp make_pair#define pir pair <ll, ll>#define pb push_back#define i128 __int128using namespace std;const ll maxn = 1e5 + 10, inf = 1e18, mod = 998244353;ll power(ll a, ll b = mod - 2, ll p = mod) {ll s = 1;while(b) {if(b & 1) s = 1ll * s * a %p;a = 1ll * a * a %p, b >>= 1;} return s;}template <class T>const inline ll pls(const T x, const T y) { return x + y >= mod? x + y - mod : x + y; }template <class T>const inline void add(T &x, const T y) { x = x + y >= mod? x + y - mod : x + y; }template <class T>const inline void chkmax(T &x, const T y) { x = x < y? y : x; }template <class T>const inline void chkmin(T &x, const T y) { x = x > y? y : x; }
} using namespace Initial;namespace Read {char buf[1 << 22], *p1, *p2;// #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, (1 << 22) - 10, stdin), p1 == p2)? EOF : *p1++)template <class T>const inline void rd(T &x) {char ch; bool neg = 0;while(!isdigit(ch = getchar()))if(ch == '-') neg = 1;x = ch - '0';while(isdigit(ch = getchar()))x = (x << 1) + (x << 3) + ch - '0';if(neg) x = -x;}
} using Read::rd;ll t, n, q, a[maxn], c[maxn], id[maxn];
ll lo[maxn], hi[maxn], mid[maxn], cst[maxn];
vector <pair <pir, ll> > _vec[maxn];
vector <pir> vc[maxn], vec[maxn];
ll h[maxn], ht; multiset <ll> st;ll calc(ll x, ll l) {ll tmp = (x >> l) << l;ll ret = (tmp << 1) - (tmp >> l - 1);tmp = x & ((1 << l) - 1);ret += (tmp << 1) - __builtin_popcount(tmp);if(tmp) {tmp = __builtin_ctz(tmp);ret += l - tmp - 1;} return ret;
}void solve() {rd(n), rd(q);for(ll i = 1; i <= n; i++) rd(a[i]);for(ll l = 1; l <= 30; l++) vec[l].clear(), _vec[l].clear();for(ll i = 1; i <= n; i++) {ll low = 0;for(ll l = 1, sum = 0; l <= i && l <= 30; l++) {chkmax(low, a[i - l + 1] << l - 1);ll high = i == l? inf : a[i - l] << l;sum += a[i - l + 1], _vec[l].pb(mkp(mkp(low, high), sum));}}for(ll l = 1; l <= 30; l++) {if(_vec[l].empty()) {vec[l].pb(mkp(inf, -inf)); continue;}sort(_vec[l].begin(), _vec[l].end()); ht = 0;for(auto t: _vec[l]) h[++ht] = t.fi.fi, h[++ht] = t.fi.se + 1;sort(h + 1, h + 1 + ht);ht = unique(h + 1, h + 1 + ht) - h - 1;for(ll i = 1; i <= ht; i++) vc[i].clear();for(auto t: _vec[l]) {ll x = lower_bound(h + 1, h + 1 + ht, t.fi.fi) - h,y = upper_bound(h + 1, h + 1 + ht, t.fi.se) - h;vc[x].pb(mkp(t.se, 1)), vc[y].pb(mkp(t.se, 0));} st.clear(); h[ht + 1] = inf + 5;if(h[1] > 1) vec[l].pb(mkp(h[1] - 1, -inf));for(ll i = 1; i <= ht; i++) {for(pir t: vc[i])if(t.se) st.insert(t.fi);else st.erase(st.find(t.fi));vec[l].pb(mkp(h[i + 1] - 1, st.empty()? -inf : *st.rbegin()));}}for(ll i = 1; i <= q; i++) rd(c[id[i] = i]);sort(id + 1, id + 1 + q, [](ll i, ll j) {return c[i] < c[j];});ll kc = 0;for(ll i = 1; i <= n; i++) chkmax(kc, a[i]);for(ll i = 1; i <= q; i++) lo[i] = kc, hi[i] = 2e9;for(ll o = 0; o <= 30; o++) {for(ll i = 1; i <= q; i++) mid[i] = lo[i] + hi[i] >> 1, cst[i] = inf;for(ll l = 1; l <= 30; l++) {// if(l == 2 && o == 30)// 	puts("GC");for(ll i = 0, j = 0; i < vec[l].size(); i++) {while(j < q && mid[id[j + 1]] <= vec[l][i].fi) {ll k = id[++j];chkmin(cst[k], calc(mid[k], l) - vec[l][i].se);}}}for(ll i = 1; i <= q; i++)if(cst[i] <= c[i]) lo[i] = mid[i] + 1;else hi[i] = mid[i] - 1;// printf("%lld %lld\n", l, res[1]);}for(ll i = 1; i <= q; i++) printf("%lld ", hi[i]); puts("");
}int main() {rd(t); while(t--) solve();return 0;
}