Dyn-scripted Robot (Hard Version)
题目链接。
Problem
Easy Version:\(K \le n\)。
Hard Version:\(K \le 10^{12}\)。
一个 \(Oxy\) 平面上有一个 \(w \times h\) 矩形,矩形的左下方有点 \((0, 0)\) ,右上方有点 \((w, h)\) 。
您还有一个最初位于点 \((0, 0)\) 的机器人和一个由 \(n\) 个字符组成的脚本 \(s\) 。每个字符都是 L、R、U 或 D,分别指示机器人向左、向右、向上或向下移动。
机器人只能在矩形内移动,否则将更改脚本 \(s\) 如下:
- 如果试图向垂直边界外移动,则会将所有
L、R取反。 - 如果尝试向水平边界外移动,则会将所有
U、D取反。
然后,它会从无法执行的字符开始执行更改后的脚本。

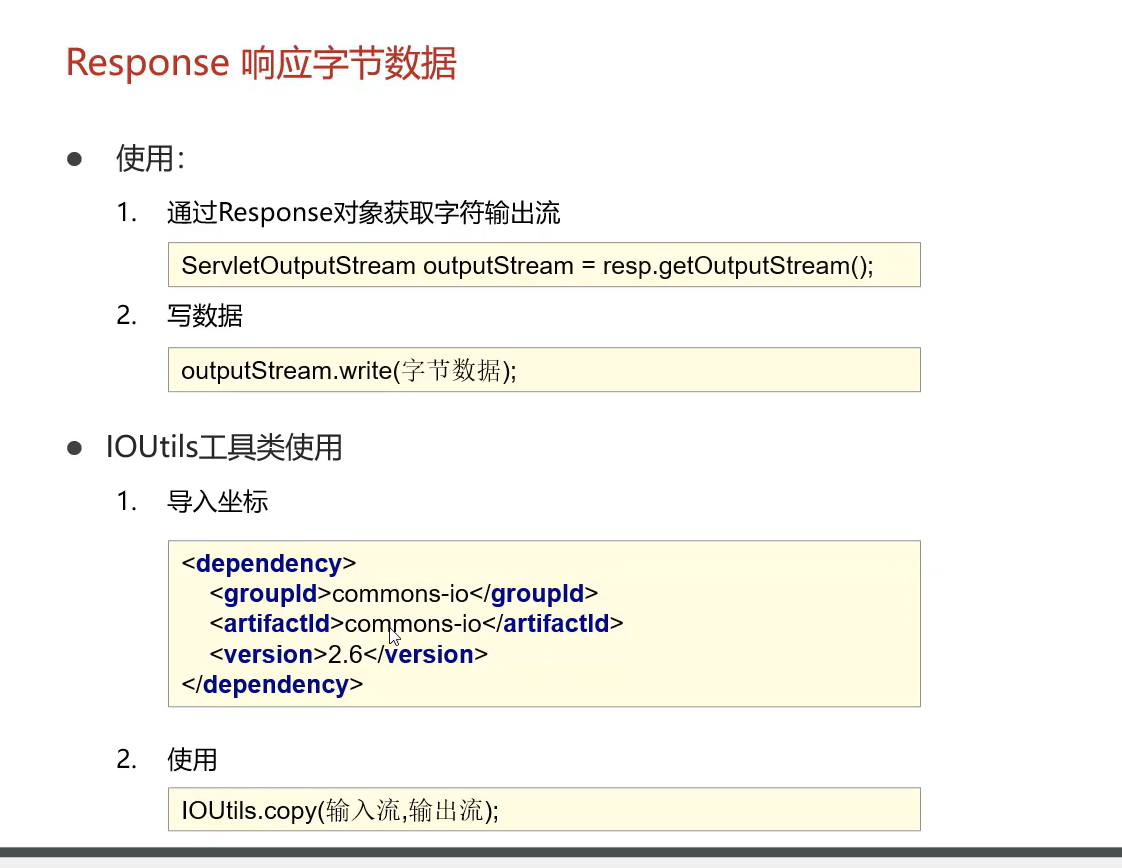
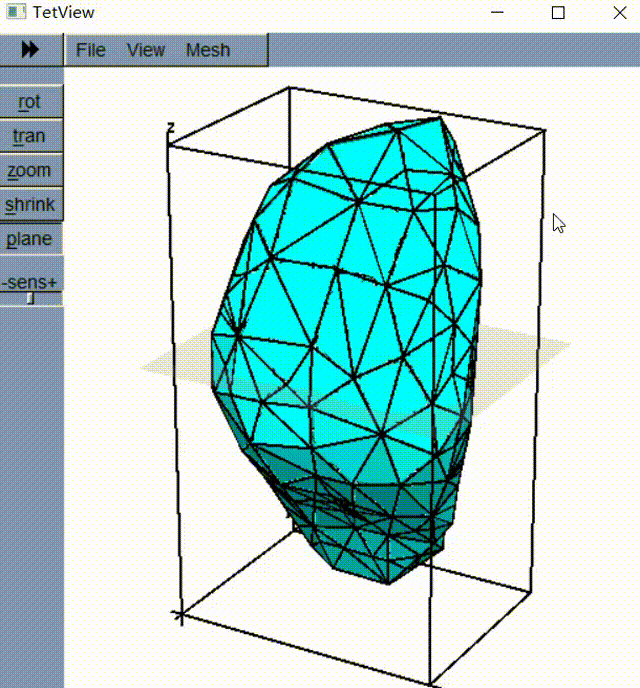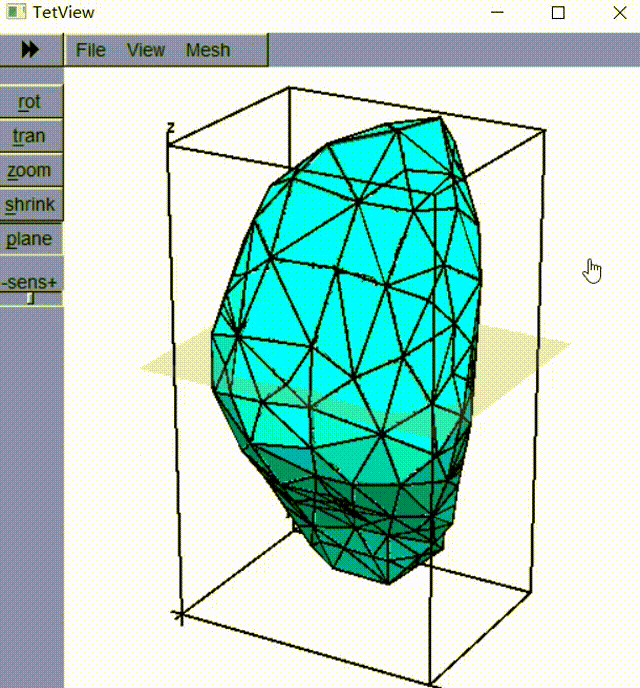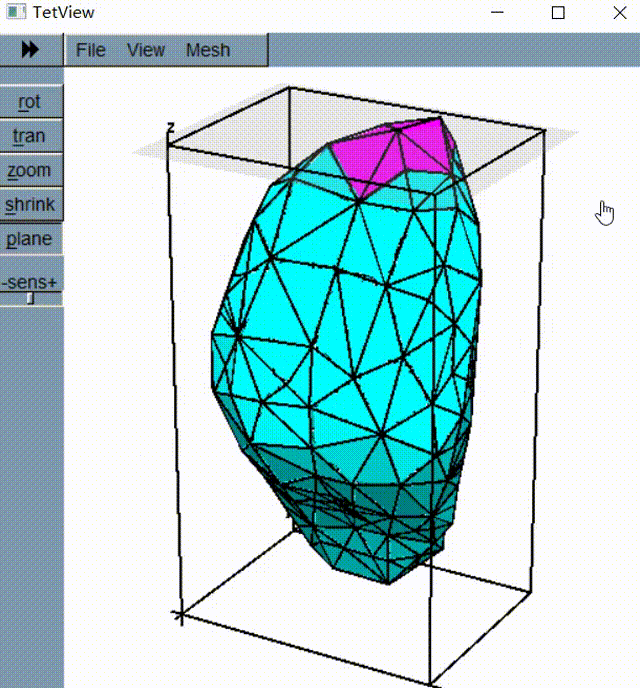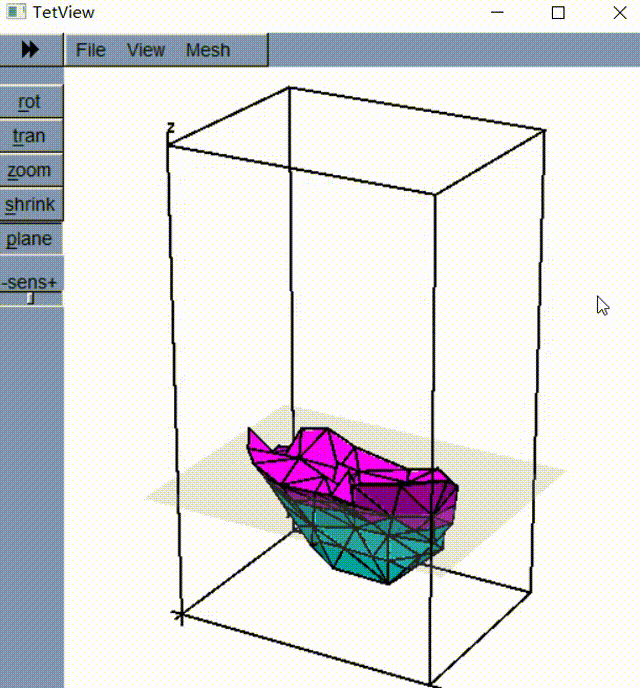
这是一个机器人移动过程的示例,其中 \(s = \texttt{"ULULURD"}\) 。
脚本 \(s\) 将被连续执行 \(K\) 次。即使重复执行,也会保留对字符串 \(s\) 的所有更改。在此过程中,机器人总共会移动到 \((0, 0)\) 点多少次?
注意,初始在 \((0,0)\) 的一次不计算在内。
数据范围:\(1\le n, w, h \le 10^6\)。
Sol
暴力显然是不可行的。发现这个东西会时刻将 LR/UD 取反是非常麻烦的。想想怎么不去反,发现抛开边界的限制,不取反就是做一个关于 \(x/y\) 轴的镜像。然后发现这个东西在 \((x, y)\) 和 \((x - 2w, y), (x, y - 2h)\) 是等价的,即在两倍意义下同余。然后就可以做了。现在要对于一个点 \((x, y)\),以及每次移动的位置 \((a, b)\),求移动 \(k\) 次的过程中,有多少次的坐标等价于 \((0, 0)\)。
然后 Easy Version 就可以直接枚举走的步数,用 map 存下每个点的位置,计算偏移量后暴力相加即可,时间复杂度:\(\mathcal{O}(K(\log w + \log h))\)。
Hard Version 也差不多。就是知道 \(x\) 在同余系下走到 \(0\) 的轮数为 \(k_0x + b_0\),\(y\) 为 \(k_1x+b_1\),大致就是最开始是第 \(b\) 轮的时候开始走,然后每 \(k\) 轮走回来。然后求的是有多少个 \(t \in [1, K]\),使得 \(\exists u,v \in [1, n] \cap \mathbb Z,t = k_0u + b_0 = k_1v + b_1\)。然后就变成了 \(k_0u - k_1v = b_0 - b_1\),直接用 exgcd 解出一组特解之后就可以直接算了。时间复杂度:\(\mathcal{O}(n \log K)\)。
感觉这场 Hard Version 能有 *2800 完全是因为这题细节有一点啊,就只是比 Easy Version 多了合并循环节的步骤。
Code
F2 Code:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
#define fi first
#define se second
mt19937_64 eng(time(0) ^ clock());
template <typename T>
T rnd(T l, T r) { return eng() % (r - l + 1) + l; }
ll exgcd(ll a, ll b, ll &x, ll &y) {if (!b)return x = 1, y = 0, a;ll d = exgcd(b, a % b, y, x);y -= a / b * x;return d;
}
ll lcm(ll x, ll y) { return x * y / __gcd(x, y); }
int n;
ll w, h, K;
int px[1000005], py[1000005];
char s[1000005];
void Solve() {scanf("%d%lld%lld%lld%s", &n, &K, &w, &h, s + 1); K--;w <<= 1, h <<= 1;px[0] = py[0] = 0;for (int i = 1; i <= n; i++) {px[i] = px[i - 1], py[i] = py[i - 1];if (s[i] == 'L') px[i]--;else if (s[i] == 'R') px[i]++;else if (s[i] == 'U') py[i]++;else py[i]--;px[i] = (px[i] % w + w) % w;py[i] = (py[i] % h + h) % h;}ll dx = px[n], dy = py[n], ans = 0;for (int i = 1; i <= n; i++) {ll x, y;ll d0 = exgcd(dx, w, x, y);if (px[i] % d0)continue;ll b0 = x * (-px[i] / d0), k0 = w / __gcd(w, dx);b0 = (b0 % k0 + k0) % k0;ll d1 = exgcd(dy, h, x, y);if (py[i] % d1)continue;ll b1 = x * (-py[i] / d1), k1 = h / __gcd(h, dy);b1 = (b1 % k1 + k1) % k1;ll d = exgcd(k0, k1, x, y), len = lcm(k0, k1) / k0, dltx = lcm(k0, k1) / k0, dlty = lcm(k0, k1) / k1;if ((b1 - b0) % d)continue;x *= (b1 - b0) / d, y *= (b1 - b0) / d;if (y < 0) {ll t = (-y + dlty - 1) / dlty;x -= t * dltx, y += t * dlty;}if (y > 0) {ll t = (y + dlty - 1) / dlty;x += t * dltx, y -= t * dlty;}if (k0 * x + b0 > K)continue;ll limx = (K - b0) / k0;ans += (limx - x) / len + 1;}printf("%lld\n", ans);
}
int main() {int T;scanf("%d", &T);while (T--)Solve();return 0;
}
F1 Code:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 7;
int n, m, W, H, m1, m2;
int s1[N], s2[N];
char str[N];
map < int, int > mp[N << 1];
void Solve() {scanf("%d%d%d%d", &n, &m, &W, &H);m1 = 2 * W, m2 = 2 * H;scanf("%s", str + 1);for (int i = 1; i <= n; ++i) {s1[i] = s1[i - 1], s2[i] = s2[i - 1];if (str[i] == 'L') s1[i] = (s1[i - 1] + 1) % m1;else if (str[i] == 'R') s1[i] = (s1[i - 1] - 1 + m1) % m1;else if (str[i] == 'U') s2[i] = (s2[i - 1] + 1) % m2;else s2[i] = (s2[i - 1] - 1 + m2) % m2;++mp[s1[i]][s2[i]];}ll ans = 0;for (int t = 0; t < m; ++t) {int r1 = (m1 - t * 1ll * s1[n] % m1) % m1, r2 = (m2 - t * 1ll * s2[n] % m2) % m2;ans += mp[r1][r2];}printf("%lld\n", ans);for (int i = 1; i <= n; ++i) mp[s1[i]].clear();
}
int main() {int T;scanf("%d", &T);while (T--) Solve();return 0;
}