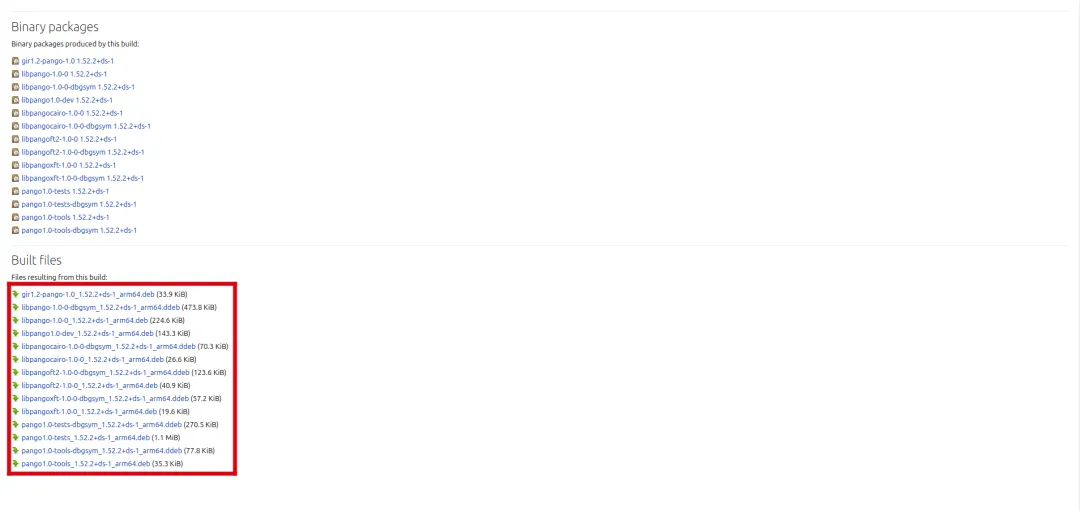
1.12
CF49E
CodeForces Link
Difficulty:2300 Tag:区间DP
#include<bits/stdc++.h>
using namespace std;
const int N=60;
string s1,s2;
bool dp1[N][N][30],dp2[N][N][30];
int dp[N][N];
map<int,vector<pair<int,int> > > mp;
int n,len1,len2;
int main(){ios::sync_with_stdio(false);cin.tie(NULL),cout.tie(NULL);cin>>s1>>s2;cin>>n;len1=s1.size(),len2=s2.size();for(int i=1;i<=n;++i){string str;cin>>str;mp[str[0]-'a'].push_back(make_pair(str[3]-'a',str[4]-'a'));}
// for(int i=0;i<mp['c'-'a'].size();++i){
// cout<<mp['c'-'a'][i].first<<' '<<mp['c'-'a'][i].second<<'\n';
// }//dp1for(int i=1;i<=len1;++i){dp1[i][i][s1[i-1]-'a']=1;}for(int l=2;l<=len1;++l){for(int i=1;i<=len1;++i){int j=i+l-1;if(j>len1){break;}for(int ch=0;ch<26;++ch){for(int k=i;k<j;++k){for(int id=0;id<mp[ch].size();++id){dp1[i][j][ch]|=dp1[i][k][mp[ch][id].first]&&dp1[k+1][j][mp[ch][id].second];}}}}}//dp2for(int i=1;i<=len2;++i){dp2[i][i][s2[i-1]-'a']=1;}for(int l=2;l<=len2;++l){for(int i=1;i<=len2;++i){int j=i+l-1;if(j>len2){break;}for(int ch=0;ch<26;++ch){for(int k=i;k<j;++k){for(int id=0;id<mp[ch].size();++id){dp2[i][j][ch]|=dp2[i][k][mp[ch][id].first]&&dp2[k+1][j][mp[ch][id].second];}}}}}//calc ansmemset(dp,0x3f,sizeof(dp));dp[0][0]=0;for(int i=1;i<=len1;++i){for(int j=1;j<=len2;++j){for(int k=1;k<=i;++k){for(int p=1;p<=j;++p){for(int ch=0;ch<26;++ch){if(dp1[k][i][ch]&&dp2[p][j][ch]){dp[i][j]=min(dp[i][j],dp[k-1][p-1]+1);}}}}}}if(dp[len1][len2]<1e9){cout<<dp[len1][len2]<<'\n';}else{cout<<"-1\n";}return 0;
}
一个区间DP的好题,总结以下关键点:
- 区间DP的一般写法:枚举区间长度,枚举两个端点,枚举其它信息,转移。
- 在计算对于两个数组的最优解时,不妨考虑从前缀的最优解进行转移,即设 \(dp_{i,j}\) 表示第一个数组前 \(i\) 和第二个数组前 \(j\) 的最优解。
- 对于两个连续字符变换为一个字符的关系,不妨将其扩展成一段区间变换为一个字符的关系,这样就能愉快的使用区间DP来求解了。
思路如何生成:
首先观察到