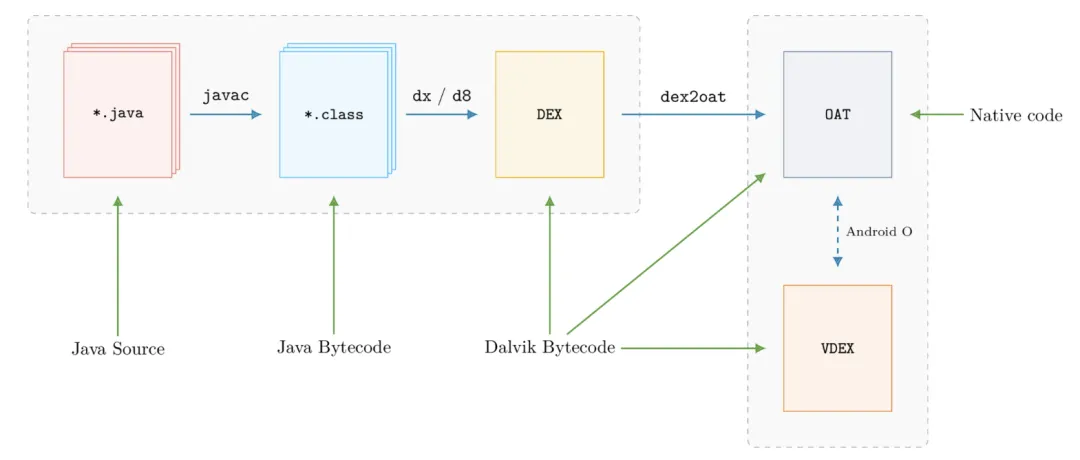
杜教筛
你现在需要求一个函数 \(f(n)\) 的前缀和 \(F(n)=\sum_{i=1}^n f(i)\) ,然后经过一些机缘巧合,你发现这个 \(f(n)\) 有以下性质:
- 存在一个积性函数 \(g(n)\) ,可以快速计算其前缀和 \(G(n)=\sum_{i=1}^n g(i)\) 。
- 数论函数 \(f\) 和 \(g\) 的狄利克雷卷积 \(h=f*g\) 的前缀和 \(H(n)=\sum_{i=1}^n h(i)\) 可以快速计算。
这样有以下式子:
所以有:
代码:(此处 \(f(n)=n\varphi(n)\),则 \(g(n)=n,h(n)=n^2\))
ll getG(ll n){if(n<=N)return sg[n];if(G.count(n))return G[n];//注意取模问题!!ll ans=n%mod*((n+1)%mod)%mod*((n+n+1)%mod)%mod*inv6%mod;for(ll l=2,r;l<=n;l=r+1){ll x=n/l;r=n/x;ans=(ans-(r-l+1)%mod*((l+r)%mod)%mod*getG(x)%mod*inv2%mod+mod)%mod;}return G[n]=ans;
}
Powerful Number 筛
你现在需要求一个积性函数 \(f(n)\) 的前缀和 \(F(n)=\sum_{i=1}^n f(i)\) ,然后经过一些机缘巧合,你发现这个 \(f(n)\) 有以下性质:
- 存在一个积性函数 \(g(n)\) ,可以快速计算其前缀和 \(G(n)=\sum_{i=1}^n g(i)\) 。
- 对于质数 \(p\),有 \(g(p)=f(p)\) 。
与杜教筛相比,你不需要找到 \(f*g\) 有什么实际含义,只需要找到一个 \(f\) 的近似函数 \(g\) ,使他两在质数部分取值相同即可。
由于 \(f,g\) 都是积性函数,所以我们可以假设有一个积性函数 \(h\) ,使其满足 \(h*g=f\) ,所以有:
然后有性质:
- 对于任意一个质数 \(p\),有 \(f(p)=g(p)h(1)+g(1)h(p)=g(p)+h(p)=f(p)+h(p)\),所以 \(h(p)=0\),由积性函数的定义,那么对于任意一个非 PN 数,其 \(h(n)=0\)。( PN 数 \(x\) 就是不存在一个 \(x\) 的质因数 \(p\),使 \(x\bmod p^2\neq 0\))
- \(n\) 以内的PN数至多 \(O(\sqrt n)\) 个,所以上面的式子在能算 \(h(p^k)(k\ge 2)\) 的情况下就可以只算 \(O(\sqrt n)\) 次就能得到 \(F(n)\) 的值。
下面就是考虑求 \(h(p^k)\) ,根据:
所以:
那么 \(h(p^k)\) 就可以递推出来,整个复杂度大概是 \(O(\sqrt n\log n)\) 的规模。
代码(此时 \(f(p^k)=p^k(p^k-1)\),那么 \(g(n)=n\varphi(n)\)):
void sous(int now,ll x,ll valh){//now表示第几个质数,x表示当前的PN数,h因为是积性函数所以valh为几个val相乘。if(now>top||x*p[now]>n||x*p[now]*p[now]>n)return;sous(now+1,x,valh);x*=p[now]*p[now];vector<ll> H;H.push_back(1);H.push_back(0);ll cf=p[now]*p[now]%mod;for(int k=2;x<=n;++k,x*=p[now],cf=cf*p[now]%mod){ll val=cf*(cf-1)%mod,cf2=1;for(int t=1;t<=k;++t,cf2=cf2*p[now]%mod){val=(val-cf2*cf2%mod*p[now]%mod*(p[now]-1)%mod*H[k-t]%mod+mod)%mod;}H.push_back(val);ans=(ans+valh*val%mod*getG(n/x)%mod)%mod;sous(now+1,x,valh*val%mod);}
}
ans=getG(n)
此外,在某些情况下,我们是可以知道 \(h(p^k)\) 具体的值的,例如上面的情况,有:
所以有 \(p^k(p^k-1)-p^{k+1}(p^{k-1}-1)=p^k(p^k-1-p^k+p)=h(p^k)-ph(p^{k-1})\) 。
得 \(\dfrac{h(p^k)}{p^k}-\dfrac{h(p^{k-1})}{p^{k-1}}=p-1\),所以 \(h(p^k)=(k-1)(p-1)p^k\)
上列推导如此复杂的原因是 \(\varphi(p^0)\neq p^{-1}(p-1)\),所以 \(\sum_{i=0}^kp^i\varphi(p^i)\neq \sum_{i=0}^kp^{i+i-1}(p-1)\),不然应该可以直接式子整体代换就可以了。
Min_25 筛
Min_25筛相比上面两种筛法,灵活性会高很多,本人感觉Min25筛更像是一种思想。
现在考虑你要求积性函数 \(f(n)\) 的前缀和 \(F(n)=\sum_{i=1}^n f(i)\) 。
我们记 \(S(n,j)\) 表示:\(\sum_{x} f(x)\),其中 \(x\) 满足:\(1\le x\le n\) 且 \(x\) 的最小质因子 \(>p_j\)(表示第 \(j\) 大的质数)。
最终 \(F(n)=S(n,0)\) ,现在考虑求 \(S(n,j)\) ,就要对满足条件的 \(x\) 进行统计。
我们将这样的 \(x\) 分成质数和合数:
-
考虑质数部分,现在我们引入 \(g(n,j)\) 表示:\(\sum_{x} f(x)\) ,其中 \(x\) 满足:\(1\le x\le n\) 且 \(x\) 要么是质数,要么其最小质因子 \(>p_j\) 。
那么这部分就是 \(g(n,\infty)\) 。
-
考虑合数部分。
因为合数部分的最小质因子都是 \(>p_j\),我们就枚举最小质数 \(p_k\) 的几次方 \(p_k^e\) ,由于 \(f(x)\) 是积性函数,那么这部分就是 \(f(p_k^e)\left(S(\dfrac{n}{p_k^e},k)+[e>1]\right)\) 。
注意上式要有值当且仅当 \(p_k^2\le n\) ,这样我们就可以极大的减少枚举的复杂度。
然后就有证明,假如如果我们已经求出 \(g(n,\infty)\) ,那么这部分的时间复杂度就是 \(O(\frac{n^{0.75}}{\log n})\) 。
现在考虑求出 \(g(n,j)\) 。
为了方便计算,我们并不直接算出 \(\sum_x f(x)\),而是将 \(f(x)\) 拆成一些完全积性函数 \(g_1(n),g_2(n)\) 的和,而且由于我们用到的只有 \(g(n,\infty)\),所以我们只需要保证对于任意质数 \(p,f(p)=g_1(p)+g_2(p)\) 就可以了。
考虑计算 \(g_1(n,j)\) 。
-
当 \(p_j^2>n\) 时, \(g_1(n,j)=g_1(n,j-1)\) 是比较显然的。
-
否则,相比 \(g_1(n,j-1)\),我们需要排除包含 \(p_j\) 为质因子的数,由于完全积性函数的性质,这部分就是 \(g_1(p_j)g_1(\frac{n}{p_j},j-1)\) 。
但需要注意 \(g_1(n,j)\) 中包含了质数,所以需要减掉 \(1\sim j-1\) 中质数的情况。
所以有转移:
但由于 \(n\) 巨大,所以想要把所有 \(g_1(n,j)\) 都求出来是不现实的。
但有一个很好的性质:所有 \(g(n,j)\) 的 \(n\) 都是最初始的 \(n\) 除上一个整数,即 \(\lfloor \frac{n}{x}\rfloor\) ,那么这样要处理的 \(g_1(n,j)\) 的总复杂度被证明是 \(O(n^{1-\epsilon})\)
例:
ll getS(ll n,int j){if(n<p[j])return 0;int id=q[n];ll val=((ll)g2[id]-g1[id]-(sp2[j]-sp1[j])+mod+mod)%mod;for(int i=j+1;i<=top&&p[i]*p[i]<=n;++i){for(ll e=p[i];e<=n;e*=p[i])val=(val+e%mod*(e%mod-1+mod)%mod*(getS(n/e,i)+(ll)(e!=p[i])))%mod;}return val;
}int main(){for(ll l=1,r;l<=n;l=r+1){ll x=n/l;r=n/x,val[q[x]=++m]=x;x%=mod;//注意这里要把1的贡献排除掉g1[m]=((1+x)*x%mod*inv2%mod-1+mod)%mod;g2[m]=(x*(x+1)%mod*(x+x+1)%mod*inv6%mod-1+mod)%mod;}for(int i=1;i<=top;++i){for(int j=1;j<=m&&p[i]*p[i]<=val[j];++j){g1[j]=(g1[j]-p[i]*(g1[q[val[j]/p[i]]]-sp1[i-1]+mod)%mod+mod)%mod;g2[j]=(g2[j]-p[i]*p[i]%mod*(g2[q[val[j]/p[i]]]-sp2[i-1]+mod)%mod+mod)%mod;}}printf("%lld\n",(getS(n,0)+1)%mod);return 0;
}