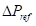AT_abc389_f [ABC389F] Rated Range 题解

题目传送门

前置知识

Treap | 线段树

解法

考虑将询问的 \(x\) 离线下来在升序排序后一起处理。

观察到每次操作只有 \(+1\)，即其之间的相对大小关系不会发生变化，此时就只需要支持将值在 \([l,r]\) 内的数加一，可以记录懒惰标记。

线段树上二分找到端点或直接 FHQ-Treap 分裂出合法区间即可。

代码

#include<bits/stdc++.h> 
#define ll long long
#define ull unsigned long long
#define sort stable_sort
#define endl '\n'
using namespace std;
int ans[300010],l[300010],r[300010];
struct BST
{int root,rt_sum=0;struct FHQ_Treap{int son[2],val,id,rnd,cnt,siz,lazy;}tree[300010];#define lson(rt) (tree[rt].son[0])#define rson(rt) (tree[rt].son[1])BST(){rt_sum=0;srand(time(0));}int build_rt(int val,int id){rt_sum++;lson(rt_sum)=rson(rt_sum)=tree[rt_sum].lazy=0;tree[rt_sum].val=val;tree[rt_sum].id=id;tree[rt_sum].rnd=rand();tree[rt_sum].cnt=tree[rt_sum].siz=1;return rt_sum;}void pushup(int rt){tree[rt].siz=tree[lson(rt)].siz+tree[rson(rt)].siz+tree[rt].cnt;}void pushlazy(int rt,int lazy){tree[rt].lazy+=lazy;tree[rt].val+=lazy;}void pushdown(int rt){pushlazy(lson(rt),tree[rt].lazy);pushlazy(rson(rt),tree[rt].lazy);tree[rt].lazy=0;}void split(int rt,int val,int &x,int &y){if(rt==0) {x=y=0;return;}pushdown(rt);if(tree[rt].val<=val){x=rt;split(rson(rt),val,rson(x),y);}else{y=rt;split(lson(rt),val,x,lson(y));}pushup(rt);}int merge(int rt1,int rt2){if(rt1==0||rt2==0)  return rt1+rt2;pushdown(rt1);pushdown(rt2);if(tree[rt1].rnd<tree[rt2].rnd){rson(rt1)=merge(rson(rt1),rt2);pushup(rt1);return rt1;}else{lson(rt2)=merge(rt1,lson(rt2));pushup(rt2);return rt2;}}void insert(int val,int id){int x,y;split(root,val,x,y);root=merge(merge(x,build_rt(val,id)),y);}void update(int l,int r){int x,y,rt;split(root,r,x,y);split(x,l-1,x,rt);pushlazy(rt,1);root=merge(merge(x,rt),y);}void dfs(int rt){if(rt==0)  return;pushdown(rt);ans[tree[rt].id]=tree[rt].val;dfs(lson(rt));dfs(rson(rt));}
}T;
int main()
{int n,m,x,i;cin>>n;for(i=1;i<=n;i++)  cin>>l[i]>>r[i];cin>>m;for(i=1;i<=m;i++){cin>>x;T.insert(x,i);}for(i=1;i<=n;i++)  T.update(l[i],r[i]);T.dfs(T.root);for(i=1;i<=m;i++)  cout<<ans[i]<<endl;return 0;
}