CudaSPONGE与PySAGES初步性能测试

技术背景

在前面的一篇博客中，我们介绍过CudaSPONGE的基础使用方法、CudaSPONGE调用Python接口函数以及CudaSPONGE结合增强采样软件PySAGES的使用方法。在这篇文章中，我们将介绍CudaSPONGE和PySAGES相结合的初步性能测试结果。

测试案例

我们沿用这一篇文章中的测试案例，对一个简单的多肽体系的两个二面角参数空间执行MetaDynamics增强采样方法：

我们的预期结果，在普通的NVT下，二面角的采样空间较为集中：

而加上PySAEGES的增强采样之后，理论上采样点可以均匀的遍布在整个采样空间：

这是我们对于这个采样结果的预期，其实图片内容也就是实际结果。但是本文主要侧重于性能测试，而我们的性能测试，就基于这个案例来开展。

调用逻辑

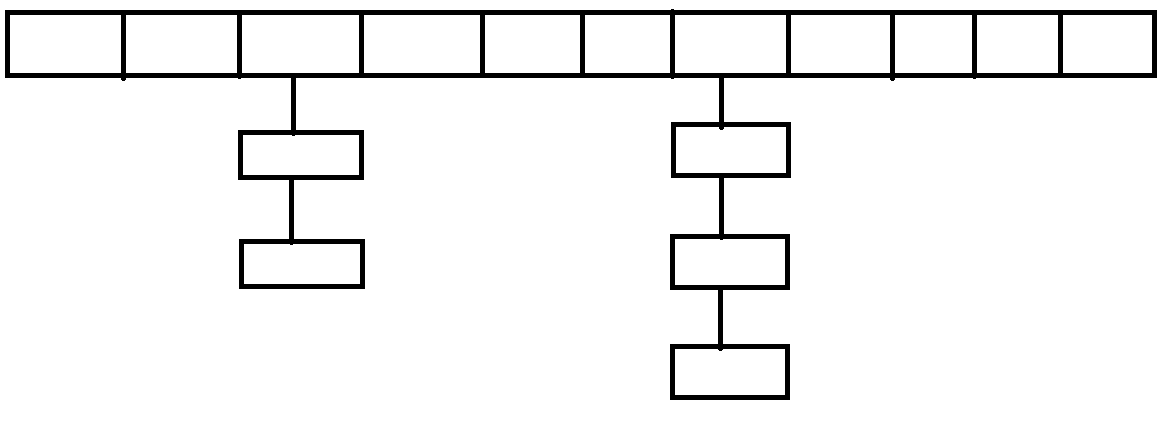
其实对于PySAGES来说，他们有自己的一套函数调用逻辑：把不同的MD软件作为Backend，由PySAGES来进行封装和调用，并且用于控制MD模拟的进行。所以如果按照PySAGES的调用逻辑来说，应该用这么一个框架来结合PySAGES和CudaSPONGE：

但是因为CudaSPONGE主要基于CUDA-C开发，为了发挥更多的性能优势，CudaSPONGE也有自己的一套调用逻辑，结合PySAGES之后是这样的：

其实这个问题的本质就在于，以哪一种软件为核心。如果以PySAGES为核心，就是采用上面的一种交互形式。如果是以MD软件为核心，就是采用下面的这种形式。不过对于CudaSPONGE v1.4版本来说，因为提供的API有限，其实只能使用下面的这种调用形式，也就是以MD软件为核心的调用形式。本文所使用到的测试案例代码，都可以参考参考链接1中的内容。

MetaDynamics说明

关于MetaDynamics的原理，建议还是翻阅一下Parrinello组的原始文章《Escaping free-energy minima》。简单的来说就是，我们在一个定义好的序参量空间，每隔固定的MD步数，就施加一个高斯势，这部分的总和组成一个偏置势：

\[V(s,t)=\int_0^td\tau w G\left[s,s(\tau)\right] \]

如果使用一个well-tempered来加速自由能面的收敛，那这个参数\(\omega\)需要从一个常数变成一个随偏置势增长而逐渐减小的一个可变量：

\[w(t)=\omega e^{-\frac{1}{\gamma -1}\beta V(s,t)} \]

这里PySAGES中的MetaDynamics就是用的这个增强采样方法，也是我们重点测试的方法对象。需要提及的是，虽然每隔固定的步数我们才会施加一个高斯势，但其实历史累积的高斯势的作用力一直都存在。所以，只要在MD过程中添加了MetaDynamics方法，就意味着每一步都需要计算一个序参量的值，及其对应的偏置势产生的偏置作用力。在很多情况下，偏置作用力的计算有可能会成为整个分子模拟过程的瓶颈部分。因此，MetaDynamics方法的性能至关重要。

初步测试数据

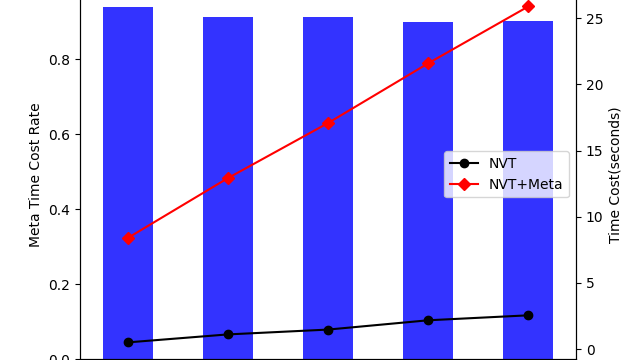
经过初步的测试，分别运行了2000、4000、6000、8000、10000个Step的NVT和Meta NVT，运行时长和Meta时长占比如下：

可以看到的是，Meta的运行时长目前可能要达到90%左右。当然，这里面影响的因素有很多，暂时还不确定性能表现与文章中描述不同的原因在哪里。因为这里面的数据传输都是使用的Dlpack进行转换，理论上可以做到Zero-Copy。不过性能后续可以再慢慢优化，就目前来说，使用PySAGES去开发一个增强采样方法，然后使用CudaSPONGE来运行分子动力学模拟的部分，开发成本相对来说是比较低的，并且获得的性能增益也不错。测试平台信息如下： ```txt GPU: RTX 3080Ti Jax: 0.3.25 Jaxlib: 0.3.25+cuda11.cudnn82 nvcc: 11.6.124 ```

总结概要

接前一篇关于PySAGES结合CudaSPONGE使用方法的文章，本文主要还是使用了一样的测试案例。仅通过不同的测试步长，来定性的分析PySAGES的MetaDynamics实现方案结合MD软件之后的性能数据。

版权声明

本文首发链接为：https://www.cnblogs.com/dechinphy/p/sponge_ext_01.html

作者ID：DechinPhy

更多原著文章：https://www.cnblogs.com/dechinphy/

请博主喝咖啡：https://www.cnblogs.com/dechinphy/gallery/image/379634.html

参考链接

1. https://www.cnblogs.com/dechinphy/p/18615556/pysages-sponge