牛客小白108 20250117-编程知识

牛客小白108 20250117

news/2025/1/20 19:17:34/文章来源:https://www.cnblogs.com/dianman/p/18682366

牛客小白108 20250117

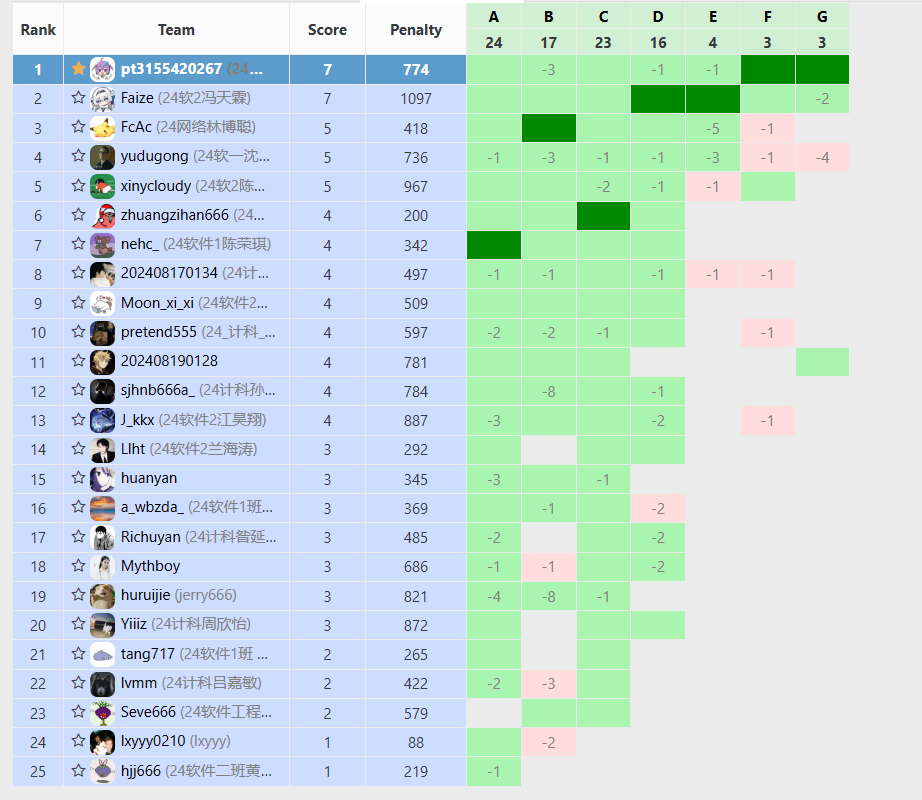
牛客小白月赛108_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ

A：

题目大意：给定 $x,y$ 第奇数次操作可以得到 $1$ ，第偶数次操作可以得到 $x$ ，求多少次操作后可以达到 $y$

#include <iostream>
using namespace std;int x, y;
bool judge(int op) {int sum = (op / 2 + op % 2) + (op / 2) * x;if (sum < y) return 1;else return 0;
}int main()
{int T;cin >> T;while (T--){cin >> x >> y;int l = -1, r = 2e9 + 1;while (l + 1 != r){int mid = l + r >> 1;if (judge(mid))l = mid;elser = mid;}cout << r << endl;}
}

二分操作数，通过下面的公式计算总数

\[sum=\frac{op}{2}*1+\frac{op}{2}*x +op\%2 \]

$op\%2$ 作用为如果操作数为奇数时，那么需要额外加 $1 $

B：

题目大意：给定一个正整数，可以对这个数进行重新排列，问这个数重新排序后能否被 $4$ 整除

#include <iostream>
#include <cstring>
#include <string>
using namespace std;void solve(void) {string s;int m[10];memset(m, 0, sizeof m);cin >> s;if (s.size() == 1) {if ((s[0] - '0') % 4 == 0) {cout << "YES" << endl;return;}else {cout << "NO" << endl;return;}}for (int i = 0; i < s.size(); i++)m[s[i] - '0']++;for (int i = 1; i <= 9; i++) {if (m[i]) {m[i]--;for (int j = 1; j <= 9; j++) {if (m[j] && (i * 10 + j) % 4 == 0) {cout << "YES" << endl;return;}}m[i]++;}}cout << "NO" << endl;return;
}int main() {int T;cin >> T;while (T--)solve();return 0;
}

能被 $4$ 整除的数满足的性质是：后两位数组成的十位数能被 $4$ 整除

使用 string 读入整数，数组模拟桶存储每个数出现的次数，特别地需要判断 s 只有一个数的情况

两层 for 循环枚举满足条件的十位数，每次枚举十位上的数时，应当在桶中把它出现的次数减去（不能重复选）

最后判断这个十位数能否被 $4$ 整除即可

C：

题目大意：给出一组元素，对元素进行分组，求满足条件的最小分组数

\[c_1 \oplus c_2\oplus \dots\oplus c_m \ne 0 \\ lcm(c_1,c_2,\dots,c_m)+c_1 \oplus c_2\oplus \dots\oplus c_m=2\times\min(c_1,c_2,\dots,c_m) \]

#include <iostream>
#include <map>
#include <string>
using namespace std;void solve(void) {map<int, int> m;int n, c;int res = 0;cin >> n;while (n--){cin >> c;m[c]++;}for (auto &[k,v] : m) res += 2 - v % 2;cout << res << endl;return;
}int main() {int T;cin >> T;while (T--)solve();return 0;
}

数学题：

\[lcm(c_1,c_2,\dots,c_m)+c_1 \oplus c_2\oplus \dots\oplus c_m=2\times\min(c_1,c_2,\dots,c_m) \]

其中的最小公倍数可以转化为

\[lcm(c_1,c_2,\dots,c_m) =k*\min(c_1,c_2,\dots,c_m) \]

两边处理后可以得到

\[c_1 \oplus c_2\oplus \dots\oplus c_m=(2-k)\times \min(c_1,c_2,\dots,c_m) \]

又因为异或的结果不能为负，且 $k>0$ ，结合第一个约束条件可以得出

\[c_1 \oplus c_2\oplus \dots\oplus c_m=\min(c_1,c_2,\dots,c_m) \]

所以每个组里面的元素都是相同的，由于 $a\oplus a=0，a\oplus a\oplus a=a$

可以作出这样的结论：每组里面的元素都是相同的，并且元素数为奇数（每个偶数都能分解为两个奇数之和）

res += 2 - v % 2

计算相同的元素分组后对答案的贡献，如果元素数为奇，贡献就是 $1$ ，如果元素数为偶，贡献就是 $2$

PS：map的遍历——结构化绑定

for (auto &[key, val] : _map) {}

在 for 循环内使用 [key, val] 的方式进行键值对遍历，其中的 key 变量对应 _map 的键，val 变量对应 _map 映射出来的值

使用 & 避免拷贝数据，加速遍历

D：

题目大意：给定一个正整数 $m$ 构造一个序列，序列中的数之和等于 $m$，$t_i$ 表示该序列中等于 $i$ 的元素个数，求 $mex\{t_1,t_2,\dots,t_n\}$，$mex$ 定义为没有出现在序列内的最小非负整数

#include<bits/stdc++.h>using namespace std;long long m;
bool judge(__int128 v){__int128 sum=(v+1)*(v+1)*v/2-v*(v+1)*(2*v+1)/6;if (sum<=m) return 1;else return 0;
}int main()
{int T;cin>>T;while (T--){cin>>m;long long l=-1,r=1e7+1;while (l+1!=r){__int128 mid=l+r>>1;if (judge(mid))l=mid;elser=mid;}cout<<r<<endl;}return 0;
}

通过贪心可以直到，能够构造出和为 $m$ 的序列的方式有两种