训练情况
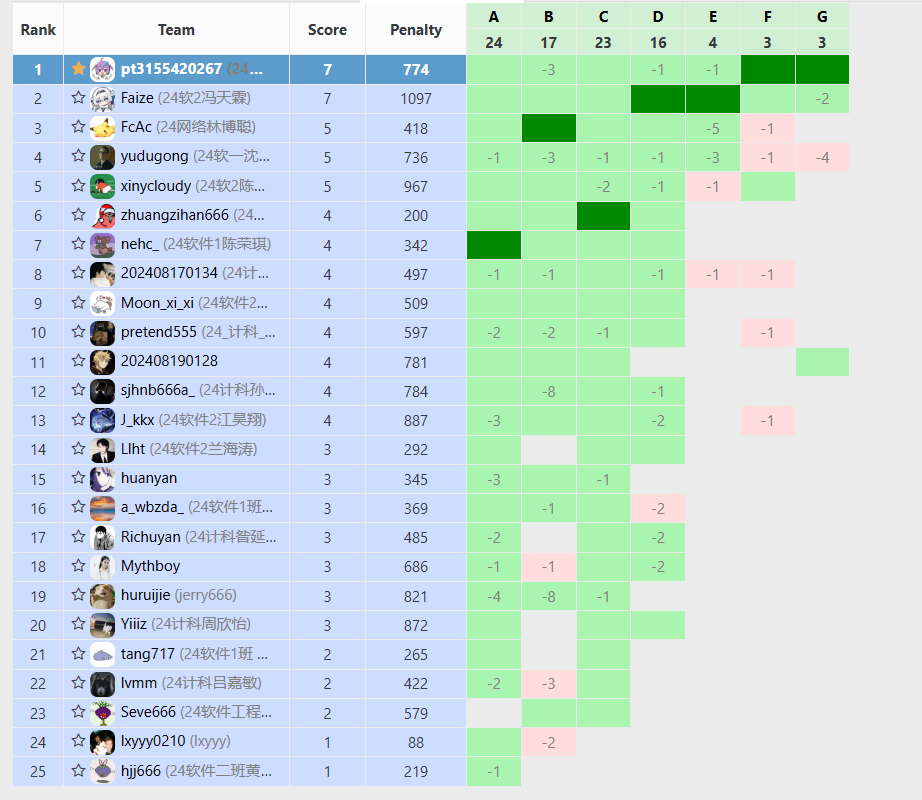
A题
给定 \((x,y)\),倒着枚举地毯的范围是否覆盖 \((x,y)\),如果覆盖直接输出,如果全部枚举完都没有则输出 -1
点击查看代码
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;int x[n+1],y[n+1],a[n+1],b[n+1];for(int i = 1;i<=n;i++){cin>>x[i]>>y[i]>>a[i]>>b[i];}int xx,yy; cin>>xx>>yy;for(int i = n;i;i--){if(xx >= x[i] && xx <= x[i]+a[i] && yy >= y[i] && yy <= y[i]+b[i]){cout<<i<<endl;return;}}cout<<-1<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
B题
求有多少对 \((P,Q)\) 使得 \(\gcd(P,Q)=x_0\),\(\operatorname{lcm}(P,Q)=y_0\)
另外有一个性质就是 \(\gcd(P,Q) \times \operatorname{lcm}(P,Q) = P \times Q\)
所以我们已知这三个条件,我们可以枚举 \(P\),然后判断是否存在一个 \(Q\) 满足上述三个条件,由于成对存在,所以我们枚举的上界只需要到 \(\sqrt{nm}\),然后 \((P,Q)\) 和 \((Q,P)\) 视为两种不同的答案,最后对数需要乘二,注意一下 \(P = Q\) 的情况要减掉
点击查看代码
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){int m,n;cin>>m>>n;int ans = 0;n*=m;for(int i=1;i<=sqrt(n);i++){if(n%i==0&&__gcd(i,n/i)==m) ans++;}cout<<ans*2-(m==n/m)<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
C题
有 \(n\) 个数,要满足 \(\lvert a_i - a_{i-1} \rvert\) 覆盖 \([1,n)\) 的所有整数,所以我们直接枚举,两个元素差的绝对值如果超过上述范围则无法满足条件,反之则存在。这题有一个小性质,排不排序都不会影响最终差绝对值覆盖的区间。
点击查看代码
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;int a[n+1];for(int i = 1;i<=n;i++) cin>>a[i];for(int i = 2;i<=n;i++){int x = abs(a[i] - a[i-1]);if(x > n-1 || x < 1){cout<<"Not jolly"<<endl;return;}}cout<<"Jolly"<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
D题
找数列中有多少对 \((i,j,k)\) 使得 \(a_i + a_j = a_k\)(\(i,j,k\) 互不相同),所以我们可以开一个数组表示某个数字是否出现过,然后枚举两个数 \(i,j\),判断是否存在 \(a_k = a_i + a_j\) 中的 \(a_k\) 是否存在,题目所述 其中有多少个数,恰好等于集合中另外两个(不同的)数之和? \(a_k\) 对答案的贡献最多为 \(1\),所以答案自增后 \(a_k\) 需要标记成没出现过
点击查看代码
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;int a[n + 1];map<int,bool> vis;for(int i = 1;i<=n;i++) cin>>a[i],vis[a[i]]=1;int ans = 0;for(int i = 1;i<=n;i++){for(int j = i+1;j<=n;j++){if(vis[a[i] + a[j]]) ans++,vis[a[i]+a[j]]=0;}}cout<<ans<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
E题
直接枚举区间 \([l,r]\) 的时间复杂度为 \(O(n^2)\) 会超时,对于区间求和的问题我们容易想到前缀和,但是我们需要处理区间是 \(k\) 的倍数,我们考虑对前缀和对 \(k\) 取模(取余数),如果位置 \(l,r\) 的前缀和 \((p_l \mod k) = (p_r \mod k)\) 则说明区间 \([l,r]\) 的和一定是 \(k\) 的倍数,因为 \((x \mod b) = ((x + kb) \mod b)\),所以我们需要统计 \(p_i\) 余数的出现次数,遍历的时候查询当前位置余数在前面出现了几次,就是有几个区间,答案加上区间个数即可,注意一下初始条件,详情见代码
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;void solve(){int n,k; cin>>n>>k;int a[n+1],pre[n+1],cnt[n+1];pre[0] = 0;for(int i = 1;i<=n;i++) cin>>a[i],cnt[i] = 0;for(int i = 1;i<=n;i++) pre[i] = pre[i-1] + a[i];for(int i = 1;i<=n;i++) pre[i] %= k;cnt[0] = 1;int ans = 0;for(int i = 1;i<=n;i++){ans += cnt[pre[i]];cnt[pre[i]]++;}cout<<ans<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
F题
求有多少对 \((i,j)\) 使得 \(a_i\) 是 \(a_j\) 的倍数,我们先统计一个数 \(x\) 在数列中的出现次数,考虑枚举 \(a_i\) 的倍数,枚举的上界为 \(k \times a_i \le max(a_i)\),如果 \(k \times a_i\) 至少出现了一次,则必定存在 \((a_i,k \times ai)\) 这一对,答案为倍数的出现次数之和,即 \(\sum{v_{k a_i}}\)
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;const int N = 5e5 + 3;int n,a[N],v[N],ma;
int ans;void solve(){cin>>n;for(int i = 1;i<=n;i++) cin>>a[i],v[a[i]]++,ma=max(ma,a[i]);for(int i = 1;i<=n;i++){for(int j = 1;a[i]*j<=ma;j++){ans+= v[a[i]*j];}}cout<<ans-n<<endl;
}signed main(){// int T; cin>>T; while(T--)solve();return 0;
}
G题
羊和狼在相邻的两个动物相同和不同时的说法是相反的,我们容易发现,只要固定了前两个动物,共有四种情况 (狼,狼)、(狼,羊)、(羊,羊)、(羊,狼),后面的动物都可以根据题目所给的说法计算出来,由于这题是一个环,所以判断首尾动物的说法是否自相矛盾,即前两只动物的说法是否和最后两只动物的说法自相矛盾,如果四种情况都自相矛盾则说明无解,否则任意输出一种合法情况均正确
点击查看代码
#include <bits/stdc++.h>using namespace std;const int N = 1e5 + 3;int n; char s[N];bool flag = false;
char ans[N];bool pd(){bool fflag = true;if(s[0] == 'o' && ans[0] == 'S'){if(ans[1] != ans[n-1]) fflag = false;}if(s[0] == 'x' && ans[0] == 'S'){if(ans[1] == ans[n-1]) fflag = false;}if(s[0] == 'o' && ans[0] == 'W'){if(ans[1] == ans[n-1]) fflag = false;}if(s[0] == 'x' && ans[0] == 'W'){if(ans[1] != ans[n-1]) fflag = false;}//if(s[n-1] == 'o' && ans[n-1] == 'S'){if(ans[0] != ans[n-2]) fflag = false;}if(s[n-1] == 'x' && ans[n-1] == 'S'){if(ans[0] == ans[n-2]) fflag = false;}if(s[n-1] == 'o' && ans[n-1] == 'W'){if(ans[0] == ans[n-2]) fflag = false;}if(s[n-1] == 'x' && ans[n-1] == 'W'){if(ans[0] != ans[n-2]) fflag = false;}return fflag;
}void mj(){for(int i = 1;i<n-1;i++){//for(int j = 0;j<n;j++) cout<<ans[j];if(ans[i] == 'S'){if(s[i] == 'o') ans[i+1] = ans[i-1];else {if(ans[i-1] == 'S') ans[i+1] = 'W';else ans[i+1] = 'S';}} else {if(s[i] == 'x') ans[i+1] = ans[i-1];else {if(ans[i-1] == 'S') ans[i+1] = 'W';else ans[i+1] = 'S';}}}
}void SS(){if(flag) return;ans[0] = 'S'; ans[1] = 'S';mj();if(pd()){flag = true;for(int i = 0;i<n;i++) cout<<ans[i];}
}void SW(){if(flag) return;ans[0] = 'S'; ans[1] = 'W';mj();if(pd()){flag = true;for(int i = 0;i<n;i++) cout<<ans[i];}
}void WS(){if(flag) return;ans[0] = 'W'; ans[1] = 'S';mj();if(pd()){flag = true;for(int i = 0;i<n;i++) cout<<ans[i];}
}void WW(){if(flag) return;ans[0] = 'W'; ans[1] = 'W';mj();if(pd()){flag = true;for(int i = 0;i<n;i++) cout<<ans[i];}
}int main(){cin>>n;cin>>s;SS();SW();WS();WW();if(!flag) cout<<-1<<endl;return 0;
}