最小生成树（学习笔记）

news/2025/1/20 19:28:37/文章来源:https://www.cnblogs.com/XichenOC/p/18682386

最小生成树\(kruskal\)

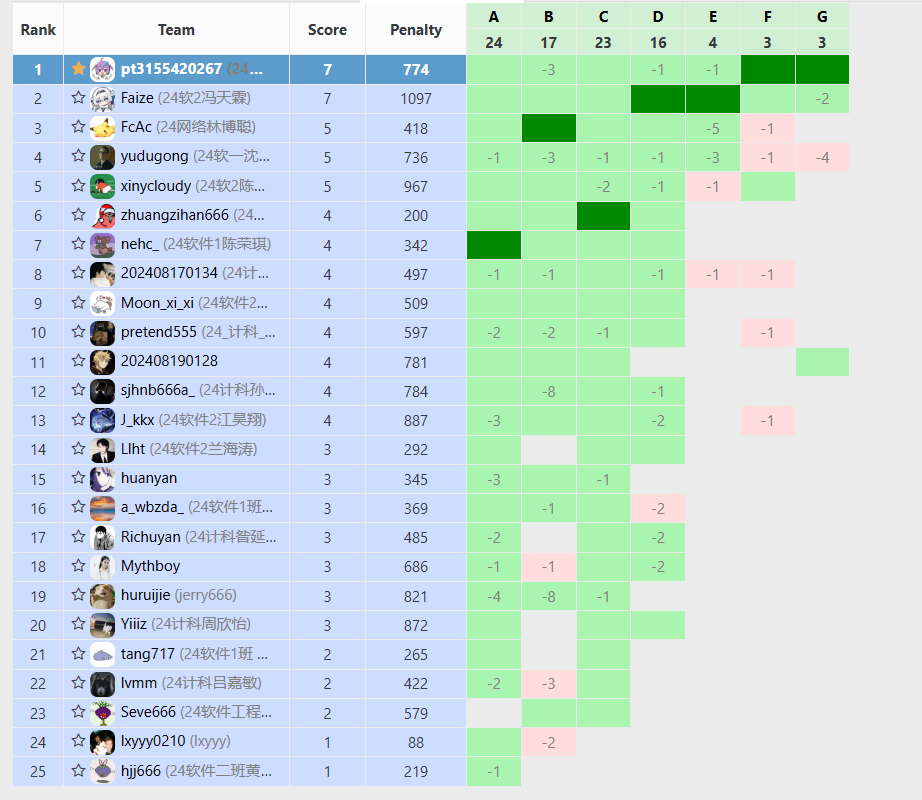
P3366 【模板】最小生成树

作用：

可以用来在一个无向连通图中找到一颗生成树，使其边权之和最小

算法原理：

\(kruskal\)运用了贪心的思想；也就是说每一次都找最短的边。因此我们只需要将所有边储存下来，再将他们从小到大进行排序，在遍历每一个边，若这个边的两个节点不在生成树中，就将他加入。这一步可以用并查集维护。每加一边就记一下数，若最后生成树的边不等于于节点数减一。那就不存在生成树；

完整代码：

#include<bits/stdc++.h>
using namespace std;
const int N=202410;
struct edge{int u,v,w;bool operator<(const edge &a)const{return w<a.w;}
}e[N];
int fa[N];
int find(int x){if(fa[x]==x)return x;return fa[x]=find(fa[x]);
}
void merge(int x,int y){fa[find(x)]=find(y);
}
int main(){int n,m;cin>>n>>m;for(int i=1;i<=n;i++){fa[i]=i;}for(int i=1;i<=m;i++){cin>>e[i].u>>e[i].v>>e[i].w;}sort(e+1,e+1+m);int ans=0,cnt=0;for(int i=1;i<=m;i++){if(find(e[i].u)!=find(e[i].v)){ans+=e[i].w;merge(e[i].u,e[i].v);cnt++;}}if(cnt!=n-1){cout<<"orz"<<endl;return 0;}cout<<ans<<endl;
}