- 代码1:stabel diffusion 代码库
- 代码2:diffusers 代码库
- 论文:High-Resolution Image Synthesis with Latent Diffusion Models
- 模型权重:runwayml/stable-diffusion-v1-5
文章目录
- 1. DDPM的通俗理解
- 1.1 DDPM的目的
- 1.2 扩散过程
- 1.3 降噪过程
- 1.4 DDPM的训练
- 1.5 DDPM 的sampling
- 1.6 DDPM中的Unet
- 2. Stable Diffusion原理
- 2.1 图片感知压缩(Perceptual Image Compression)
- 2.1.1 动机
- 2.1.2 方法
- 2.1.3 训练
- 2.2 潜在扩散模型(Latent Diffusion Models)
- 2.3 条件机制(Conditioning Mechanisms)
- 2.4 模型测评
- 2.5 小结
- 3. 参考
前一篇文章Stable Diffusion XL(SDXL)原理详解讲解了SDXL的原理以及相对SD1.x的改进点,但并未涉及SD的理论,本文将以简单易懂的方式介绍stable diffusion及其背后的相关原理,让大家能够通俗的理解SD在做什么,其中涉及DDPM的很多地方我们直接讲结论,具体的数学推导见下一篇文章。
1. DDPM的通俗理解
Stable Diffusion等扩散模型背后的主要原理就是扩散模型了,而此处的扩散模型主要是指DDPM,本文将以简单易懂的方式来讲解DDPM,尽量不涉及公式推导,具体的推导我们将在后面一篇文章中详细讲解。
1.1 DDPM的目的
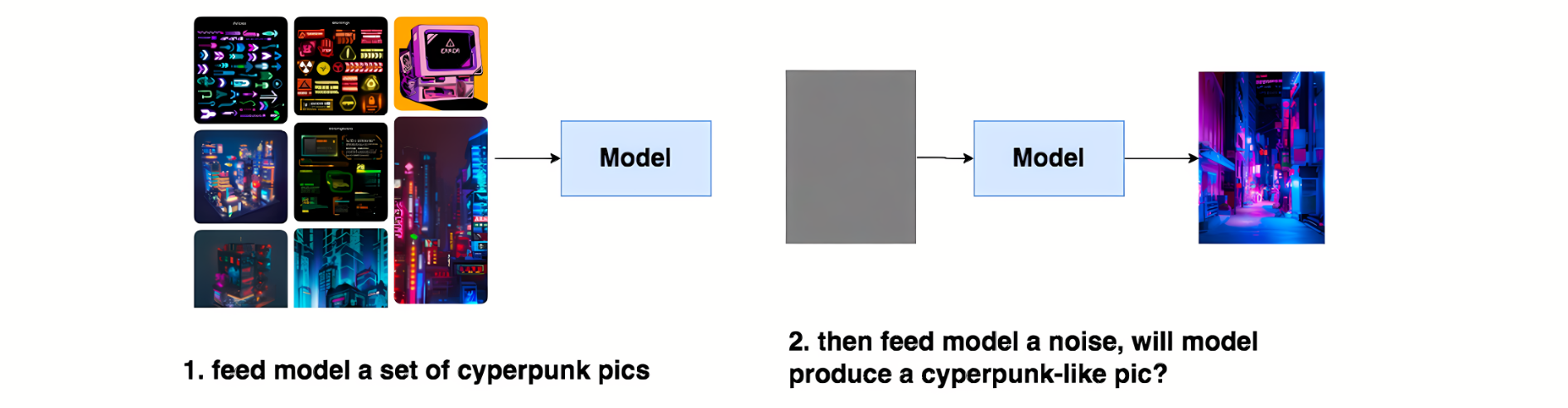
DDPM的本质作用,就是学习训练数据的分布,产出尽可能符合训练数据分布的真实图片,通俗的说就是给模型喂一堆cyperpunk风格的图片,让模型学会cyberpunk风格的分布信息,然后喂给模型一个随机噪音,就能让模型产生一张逼真的cyberpunk照片。
DDPM算法整个过程包括两步:
- Diffusion Process (又被称为Forward Process) 扩散过程
- Denoise Process(又被称为Reverse Process)降噪过程
扩散模型的整体流程如下图所示,一步步加噪的过程,就被称为Diffusion Process;一步步去噪的过程,就被称为Denoise Process
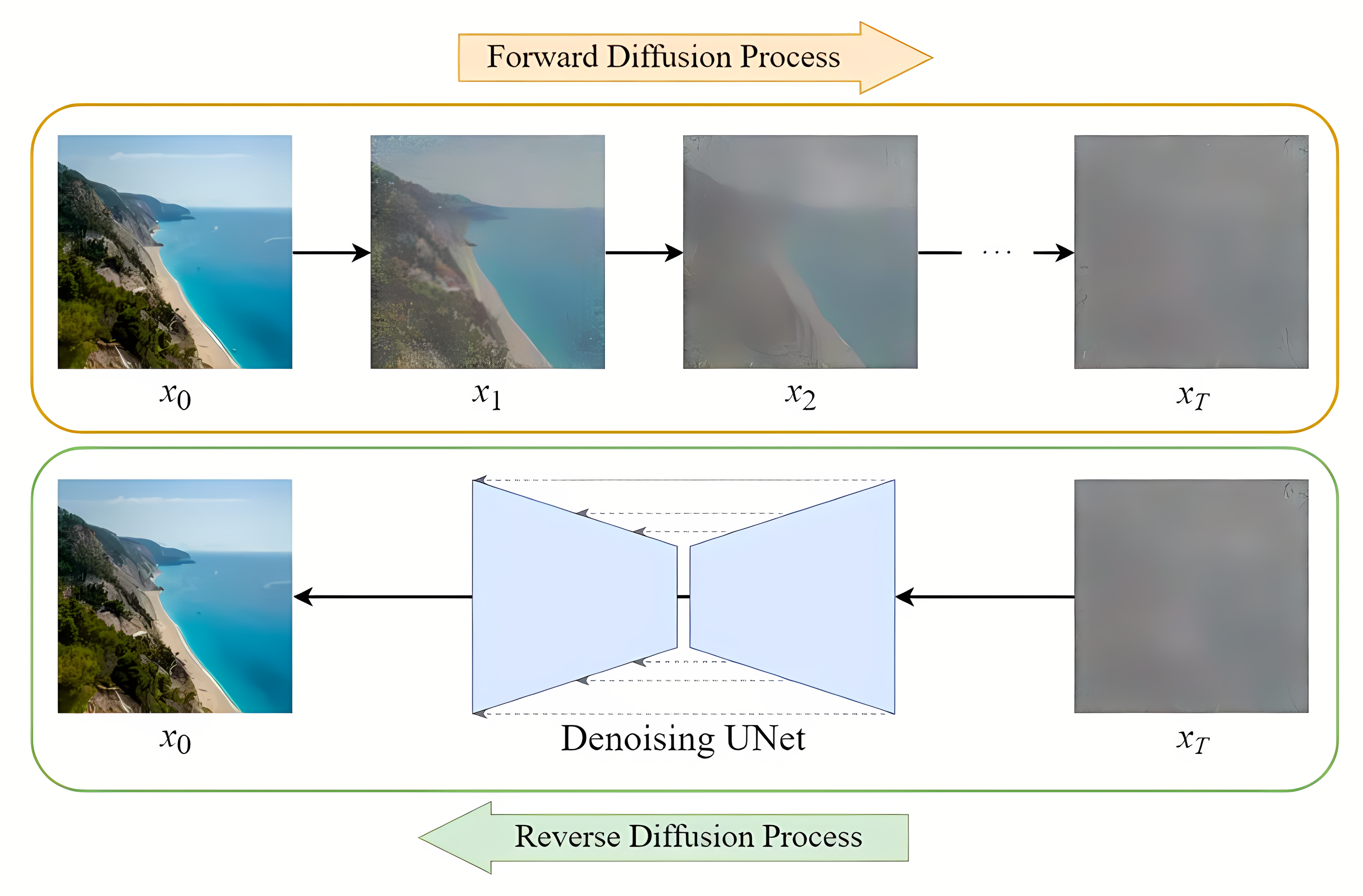
1.2 扩散过程
如图所示,进行了1000步的加噪,每一步我们都往图片上加入一个高斯分布的噪声,直到图片变为一个基本是纯高斯分布的噪声
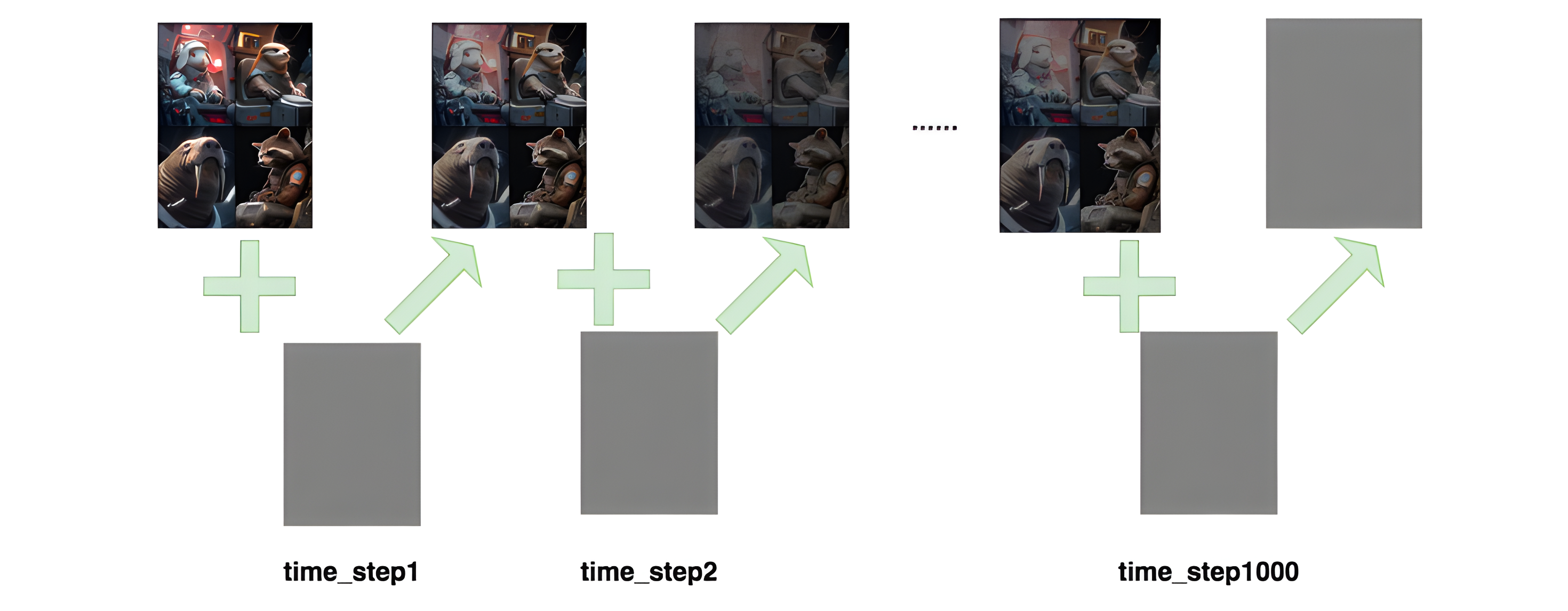
记
- T T T :加噪总的步数
- x 0 , x 1 , x 2 , . . . , x T x_0, x_1, x_2, ... , x_T x0,x1,x2,...,xT:为每步加噪后的图片,其中 x 0 x_0 x0是原始图片, x T x_T xT是第 T T T步加噪后的图片
- ϵ ∈ N ( 0 , I ) \epsilon \in N(0, I) ϵ∈N(0,I) 是每一步加的噪声
那个根据上图所示:
x T = x t − 1 + ϵ = x 0 + ϵ 0 + ϵ 1 + . . . + ϵ t x_T = x_{t-1}+\epsilon = x_0+\epsilon_0+\epsilon_1+...+\epsilon_t xT=xt−1+ϵ=x0+ϵ0+ϵ1+...+ϵt
根据上式,为了得到 x T x_T xT需要sample多次噪声,比较麻烦。因此使用 重参数化技巧 来简化,sample一次噪声直接从 x 0 x_0 x0得到 x t x_t xt。即如下式所示(注意在本文中不进行公式推导,直接讲结论,给大家来对扩散模型一个直观的理解,所有公式将在下一篇文章中进行推导):
x t = α ˉ t x 0 + 1 − α ˉ t ϵ x_{t}={\sqrt{{\bar{\alpha}}_{t}}}x_{0}+{\sqrt{1-{\bar{\alpha}}_{t}}}\epsilon xt=αˉtx0+1−αˉtϵ
其中 α ˉ t = α 1 α 2 . . . α t \bar\alpha_{t}=\alpha_{1}\alpha_{2}...\alpha_{t} αˉt=α1α2...αt; α t = 1 − β t \alpha_t=1-\beta_t αt=1−βt; β 1 , β 2 . . . β t \beta_1, \beta_2 ... \beta_t β1,β2...βt 是一系列常数,是我们直接设定的超参数,随着T的增加越来越大。这样 α t \alpha_t αt随着 T T T增大而减小, α ˉ t \bar\alpha_{t} αˉt随着 T T T增大而减小。对上式的一个直观解释为:随着步数的增加,图片中原始信息含量越少,噪声越多,因此给原始图片权重越来越小,给噪声一个越来越大的权重。
1.3 降噪过程
降噪过程就是给定 x t x_t xt,让模型能把它还原到 x t − 1 x_{t-1} xt−1。通常加噪过程表示为 q ( x t ∣ x t − 1 ) q(x_t|x_{t-1}) q(xt∣xt−1),而去噪过程表示成 p ( x t − 1 ∣ x t ) p(x_{t-1}|x_t) p(xt−1∣xt)。由于加噪过程只是按照设定好的超参数进行前向加噪,本身不经过模型。但去噪过程是真正训练并使用模型的过程。所以更进一步,用 p θ ( x t − 1 ∣ x t ) p_{\theta}(x_{t-1}|x_t) pθ(xt−1∣xt) 来表示去噪过程,其中 θ \theta θ 表示模型参数。
具体反向过程如下图所示,从第T个timestep开始,模型的输入为 x t x_t xt 与当前timestep T T T。模型是一个噪声预测器(网络结构为UNet),它会根据当前的输入预测出噪声,然后将当前图片减去预测出来的噪声,就可以得到去噪后的图片 x t − 1 x_{t-1} xt−1。重复这个过程,直到还原出原始图片 x 0 x_0 x0为止:
由于模型每一步的去噪都用的是同一个模型,所以必须告诉模型,现在进行的是哪一步去噪。因此引入timestep。timestep的表达方法类似于Transformer中的位置编码,将一个常数转换为一个向量,再和我们的输入图片进行相加。
1.4 DDPM的训练
如上文所述,UNet模型是DDPM的核心架构,DDPM模型训练的目的是给定time_step和加噪的图片,结合两者去预测图片中的噪声。现在我们已知:
- 第t个时刻的输入图片可以表示为: x t = α ˉ t x 0 + 1 − α ˉ t ϵ x_{t}={\sqrt{{\bar{\alpha}}_{t}}}x_{0}+{\sqrt{1-{\bar{\alpha}}_{t}}}\epsilon xt=αˉtx0+1−αˉtϵ
- 第t个时刻sample出的噪声(即真实噪声)为: ϵ ∈ N ( 0 , I ) \epsilon \in N(0, I) ϵ∈N(0,I)
- Unet模型预测出来的噪声为: ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ , t ) \epsilon_\theta({\sqrt{{\bar{\alpha}}_{t}}}x_{0}+{\sqrt{1-{\bar{\alpha}}_{t}}}\epsilon, t) ϵθ(αˉtx0+1−αˉtϵ,t),其中 θ \theta θ 为模型参数
那么损失函数可以表示成:
l o s s = ϵ − ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ , t ) loss=\epsilon-\epsilon_\theta({\sqrt{{\bar{\alpha}}_{t}}}x_{0}+{\sqrt{1-{\bar{\alpha}}_{t}}}\epsilon, t) loss=ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)
我们的训练目标就是最小化该损失,当然该损失也可写成MSE的形式。
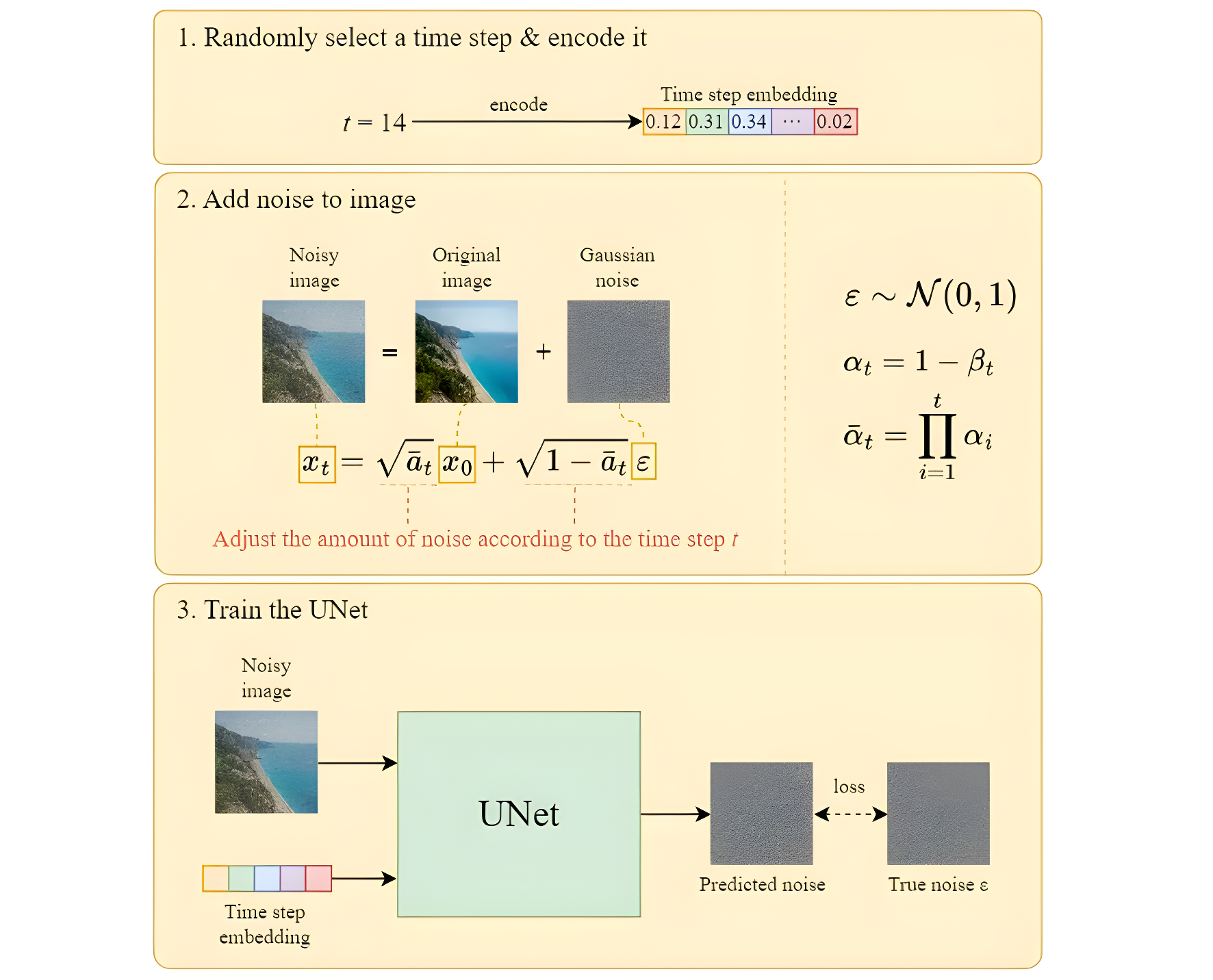
如上图所示,整个训练过程如下:
- 从训练数据中,抽样出一条 x 0 x_0 x0
- 随机抽样出一个timestep t t t。( t ∈ Uniform ( 1 , 2 , 3... , T ) t \in \text {Uniform}(1, 2, 3 ..., T) t∈Uniform(1,2,3...,T))
- 随机抽样出一个噪声 ϵ ∈ N ( 0 , I ) \epsilon \in N(0, I) ϵ∈N(0,I)
- 计算损失: l o s s = ϵ − ϵ θ ( α ˉ t x 0 + 1 − α ˉ t ϵ , t ) loss=\epsilon-\epsilon_\theta({\sqrt{{\bar{\alpha}}_{t}}}x_{0}+{\sqrt{1-{\bar{\alpha}}_{t}}}\epsilon, t) loss=ϵ−ϵθ(αˉtx0+1−αˉtϵ,t)
- 计算梯度,更新模型,重复上面过程,直至收敛
以上是一个数据计算,也可按整个batch计算
1.5 DDPM 的sampling
所谓sampling就是推理过程,对于训练好的模型,我们从最后一个时刻(T)开始,传入一个纯噪声(或者是一张加了噪声的图片),逐步去噪。根据 x t = α ˉ t x 0 + 1 − α ˉ t ϵ x_{t}={\sqrt{{\bar{\alpha}}_{t}}}x_{0}+{\sqrt{1-{\bar{\alpha}}_{t}}}\epsilon xt=αˉtx0+1−αˉtϵ 可以推导出 x t − 1 x_{t-1} xt−1:
x t − 1 = 1 α t ( x t − 1 − α t 1 − α ˉ t ϵ θ ( x t , t ) ) \mathbf{x}_{t-1}=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right) xt−1=αt1(xt−1−αˉt1−αtϵθ(xt,t))
为了增加推理中的随机性,额外增添一项,从而得到下式:
x t − 1 = 1 α t ( x t − 1 − α t 1 − α ˉ t ϵ θ ( x t , t ) ) + σ t z \mathbf{x}_{t-1}=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)+\sigma_t \mathbf{z} xt−1=αt1(xt−1−αˉt1−αtϵθ(xt,t))+σtz
如下图所示,从时间步T开始,输入模型纯噪声 x T x_T xT和时间步 t t t,预测该时间步的噪声 ϵ t = ϵ θ ( x T , t ) \epsilon_t=\epsilon_{\theta}(x_{T}, t) ϵt=ϵθ(xT,t),然后得到 x t − 1 = x t − ϵ t x_{t-1}=x_t-\epsilon_t xt−1=xt−ϵt,将其输入到模型中再预测噪声,直到得到 x 0 x_0 x0。
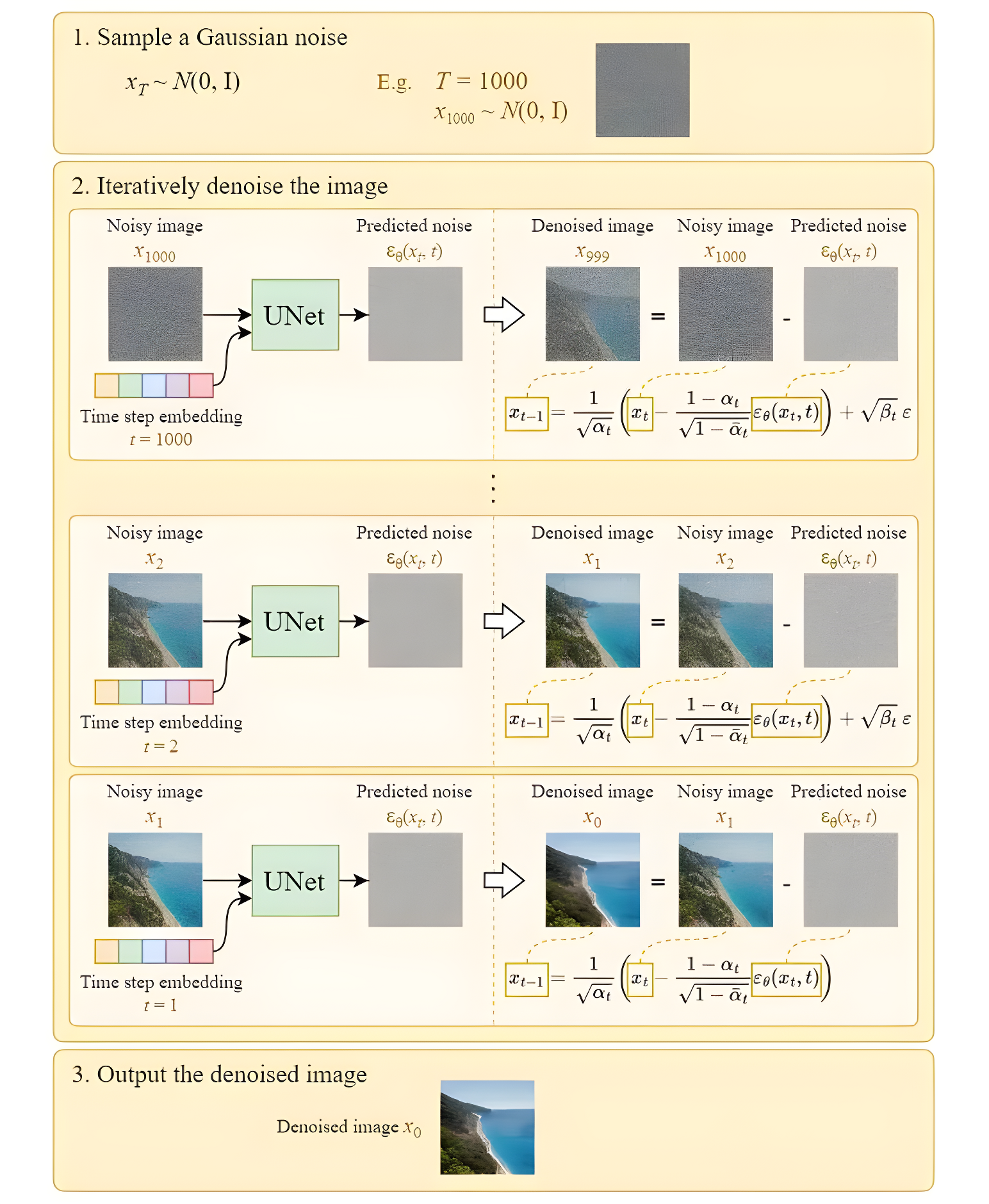
1.6 DDPM中的Unet
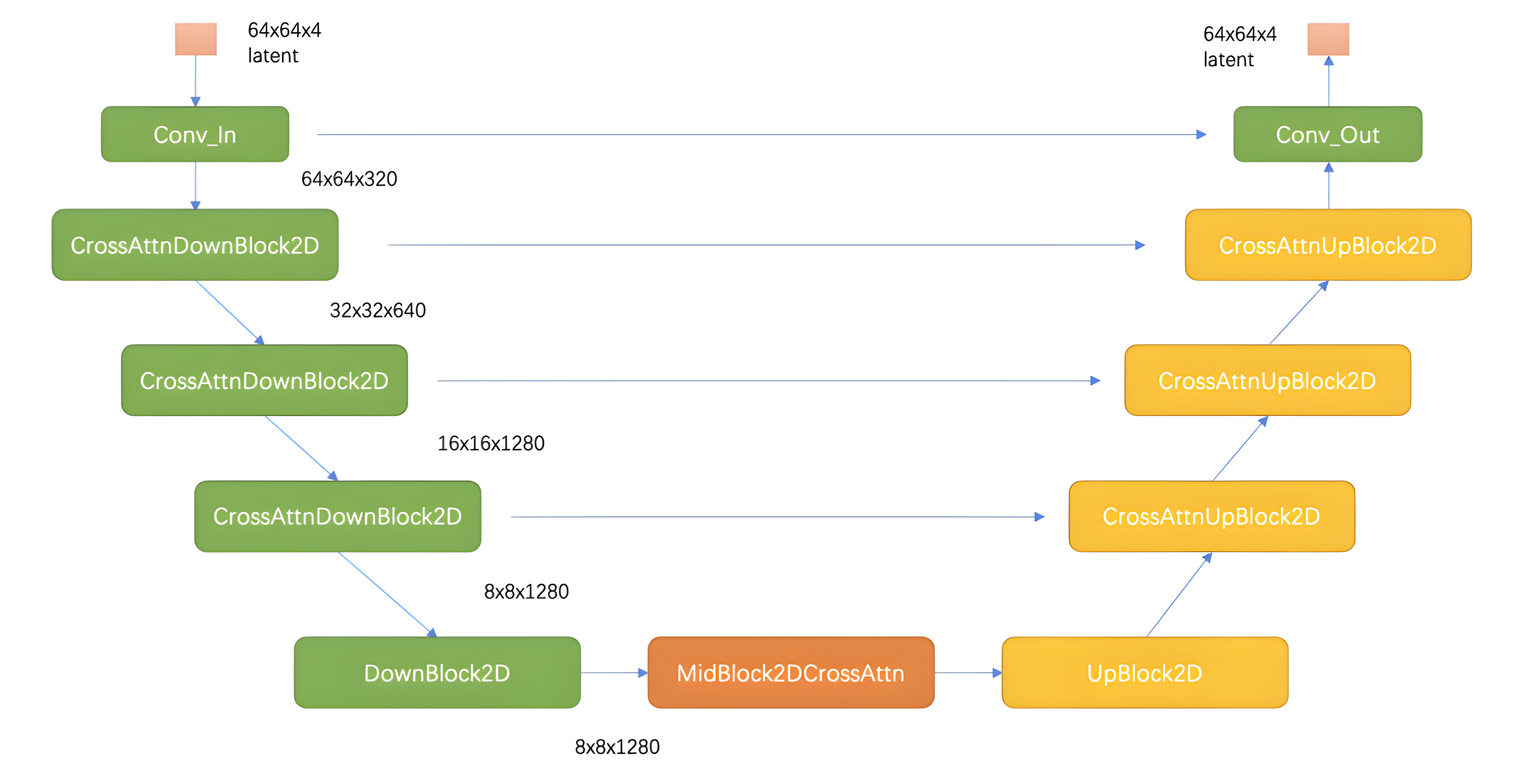
如下图所示,Unet主要包括三部分,左边绿色的encoder部分,中间橙色的MidBlock部分,以及右边黄色的decoder部分。在Encoder部分中,UNet模型会逐步压缩图片的大小;在Decoder部分中,则会逐步还原图片的大小。同时在Encoder和Deocder间,还会使用“残差连接”(虚线部分),确保Decoder部分在推理和还原图片信息时,不会丢失掉之前步骤的信息。下图展示了输入为32*32*3的图片,在DDPM的Unet中的流程,其中红色箭头是下采样,绿色箭头为上采样,蓝色箭头代表卷积操作和attention操作。
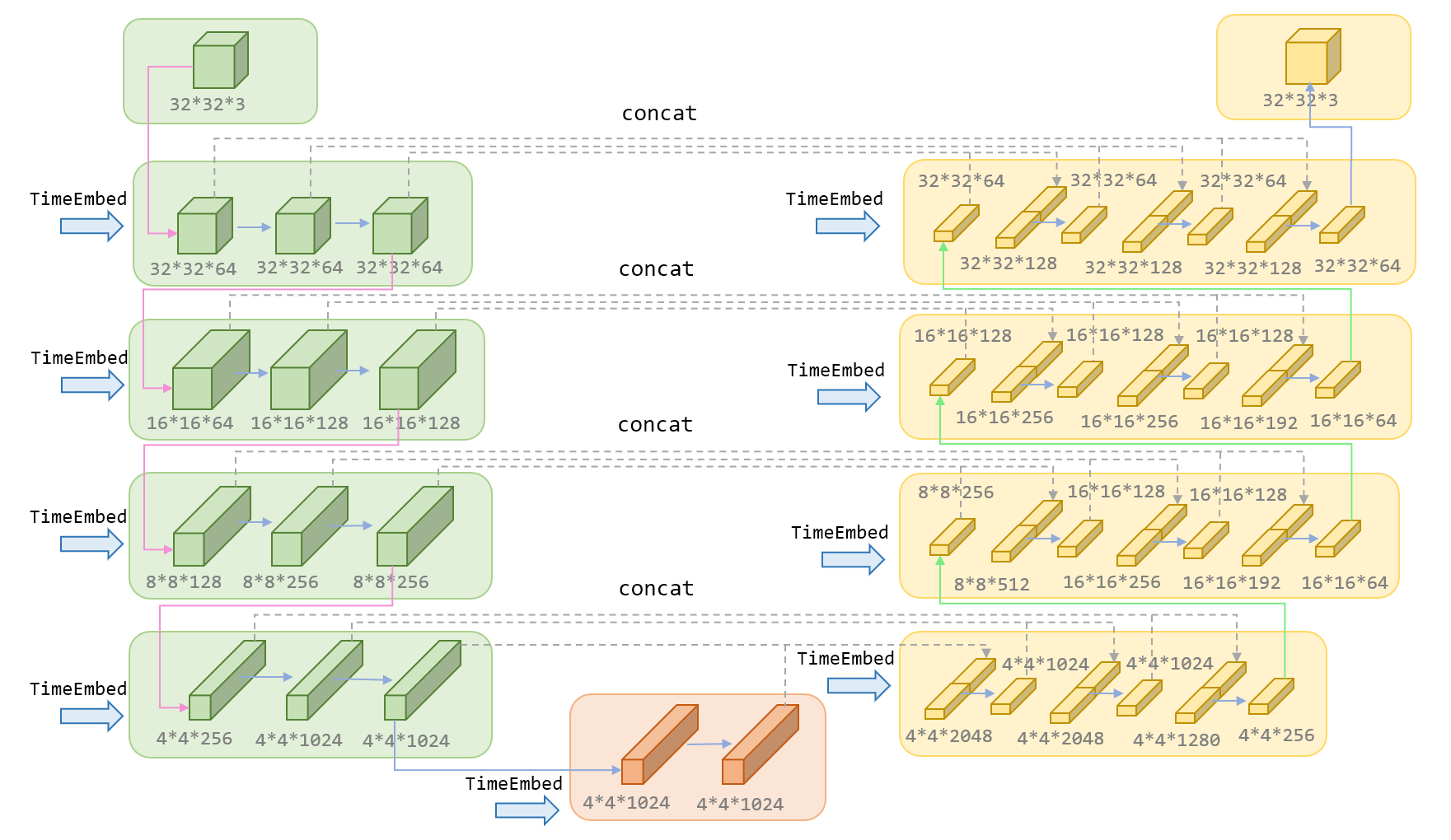
上图中蓝色箭头部分,不仅仅有卷积操作还有self-attention操作,具体如下图所示,TimeEmbedding层采用和Transformer一致的三角函数位置编码,将常数转变为向量。Attention层则是沿着channel维度将图片拆分为token,做完attention后再重新组装成图片。
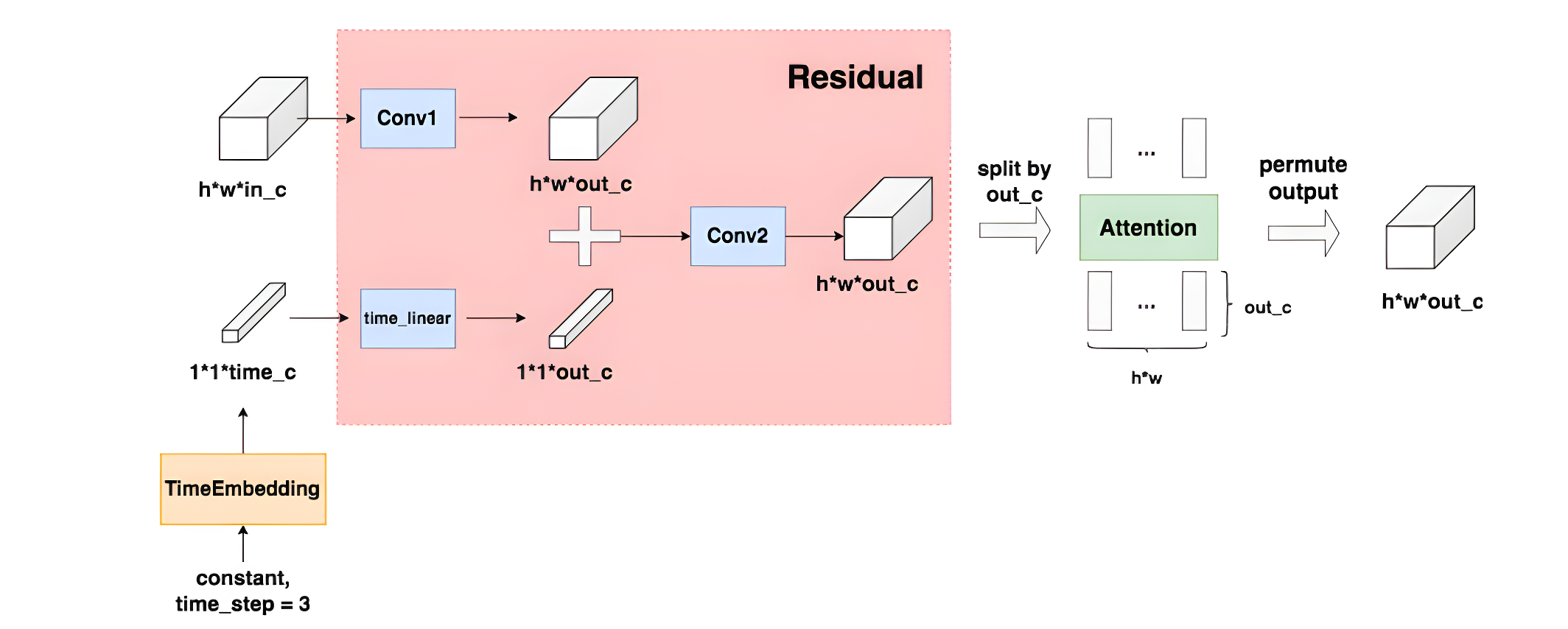
2. Stable Diffusion原理
上文中提到的扩散模型,在扩散(采样)过程会向U-Net提供完整尺寸的图像来获得最终结果。这使得纯扩散模型在总扩散步数T和图像大小较大时生成图像极其缓慢,Stable Diffusion 因此而诞生。
Stable Diffusion的最大贡献主要有如下两点:
- Diffusion model相比GAN可以取得更好的图片生成效果,但是Diffusion Model训练和推理代价都很高,需要更大的显存和计算资源。SD提出在潜在表示空间(latent space)上进行diffusion过程的方法,从而能够大大减少计算复杂度,同时也能达到十分不错的图片生成效果
- SD通过cross-attention的方法来实现多模态训练,使得条件图片生成任务也可以实现。SD中条件图片生成任务包括类别条件图片生成(class-condition), 文图生成(text-to-image), 布局条件图片生成(layout-to-image)等
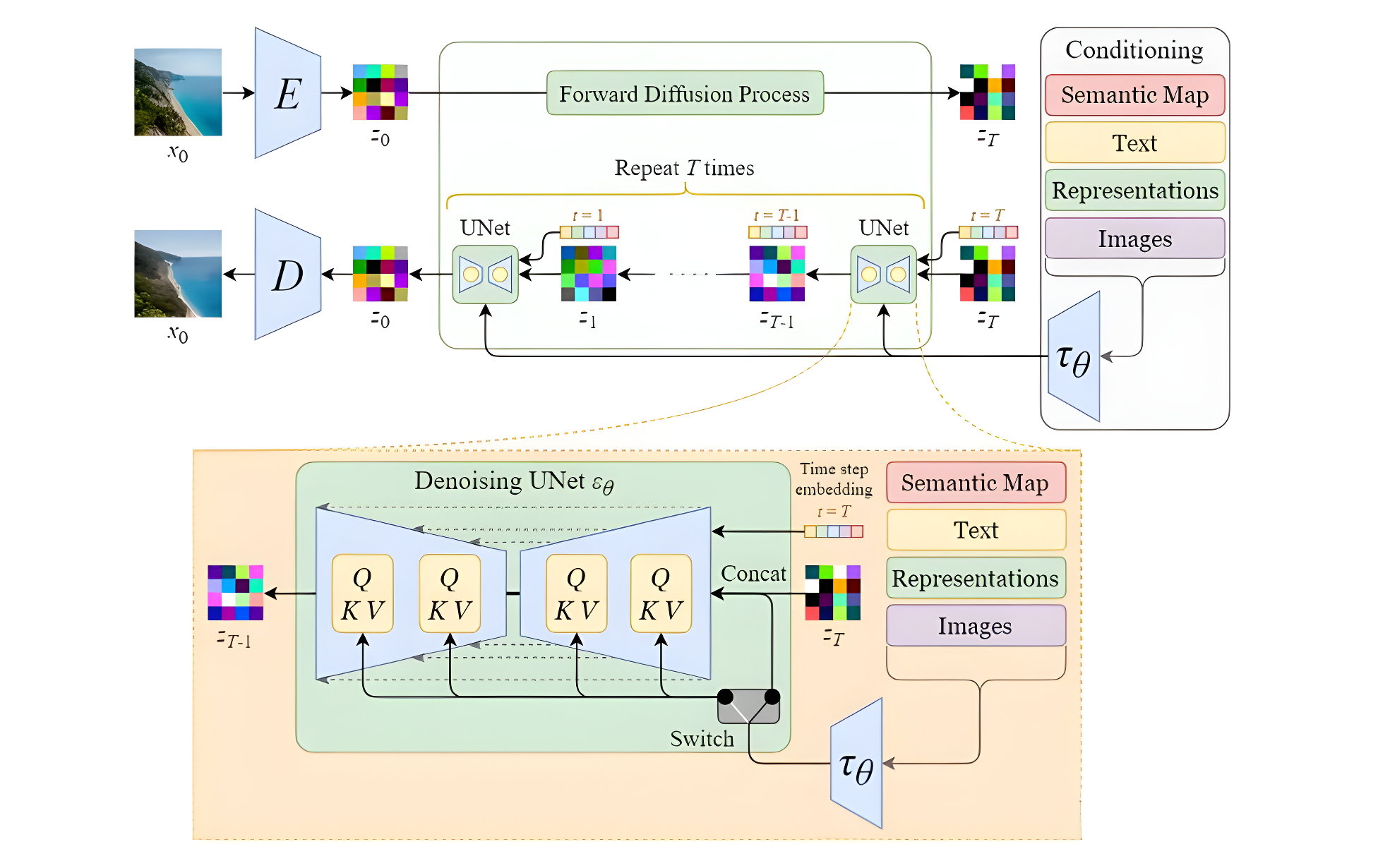
Stable Diffusion的结构如下图所示,主要由AutoEncoder、扩散模型和Condition条件模块三部分组成。具体方法是首先需要训练好一个自编码模型(AutoEncoder,包括一个编码器 E E E和一个解码器 D D D )。之后利用编码器对图片进行压缩,然后在潜在表示空间上做diffusion操作,最后我们再用解码器恢复到原始像素空间即可,论文将这个方法称之为感知压缩(Perceptual Compression)。
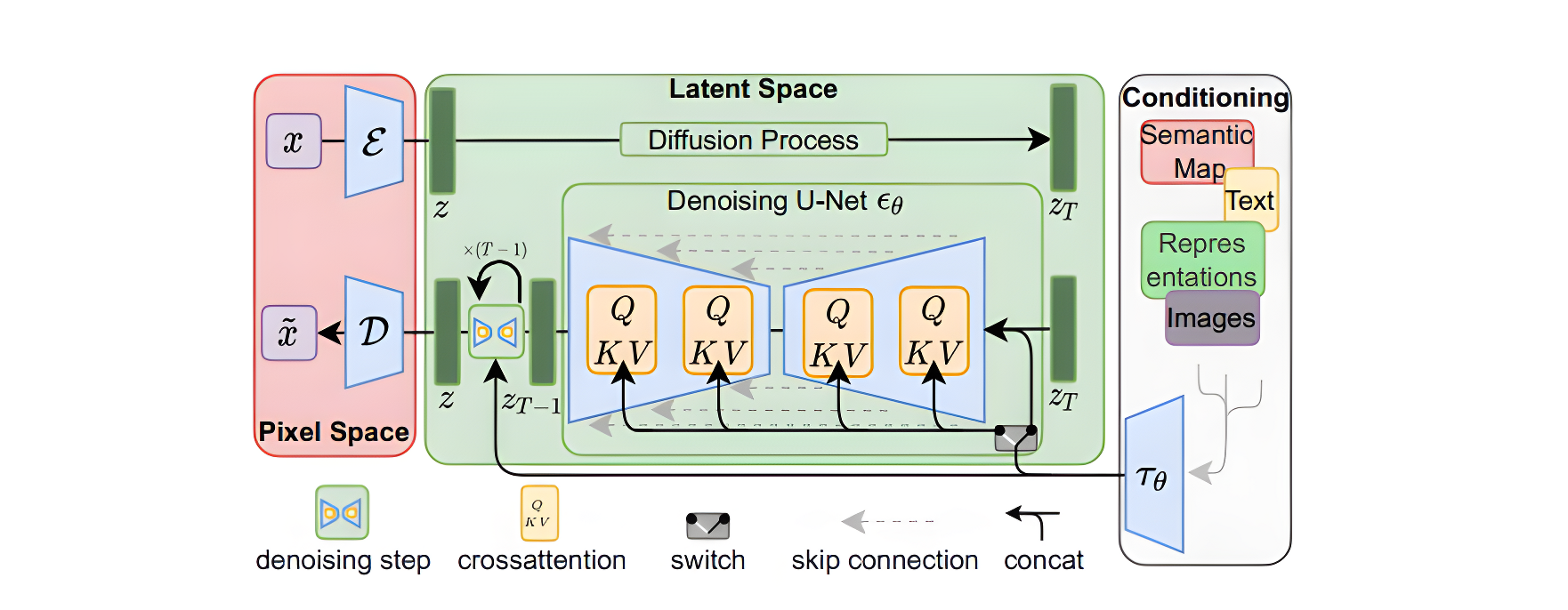
在潜在表示空间上做diffusion操作其主要过程和标准的扩散模型没有太大的区别,所用到的扩散模型的具体实现为 time-conditional UNet。但是有一个重要的地方是SD引入了条件机制(Conditioning Mechanisms),通过cross-attention的方式来实现多模态训练,使得条件图片生成任务也可以实现。下面对三个模块进行详细分析
2.1 图片感知压缩(Perceptual Image Compression)
图片感知压缩实际就是使用VAE来编码和解码图片,VAE相关内容看查看之前的文章从VAE到Diffusion生成模型详解(1):变分自编码器VAE
2.1.1 动机
感知压缩本质上是一个tradeoff,非感知压缩的扩散模型由于在像素空间上训练模型,若期望生成一张高分辨率图片,意味着训练的空间也是一个很高维的空间,从而训练过程中计算成本非常大。引入感知压缩是通过VAE这类自编码模型对原图片进行处理,忽略掉图片中的高频信息,只保留重要、基础的一些特征,将高维图片压缩到一个低维表示,然后在低维空间上进行训练,从而能够大幅降低训练和采样阶段的计算复杂度,让文图生成等任务能够在消费级GPU上,在10秒级别时间生成图片,大大降低了落地门槛。
感知压缩主要利用一个预训练的自编码模型,该模型能够学习到一个在感知上等同于图像空间的潜在表示空间,但是维度确比原始图像小很多。这样只需要训练一个通用的自编码模型,就可以用于不同的扩散模型的训练,在不同的任务上使用。
2.1.2 方法
基于感知压缩的扩散模型的训练本质上是一个两阶段训练的过程,第一阶段训练一个自编码器,第二阶段才需要训练扩散模型本身。在第一阶段训练自编码器时,为了防止得到的latent的标准差过大,作者使用了两种正则化方法,一种是KL-reg,另一种是VQ-reg,因此在官方发布的一阶段预训练模型中,会看到KL和VQ两种实现。在Stable Diffusion中主要采用AutoencoderKL这种实现。
具体来说,给定图像 x ∈ R H × W × 3 x\in\mathbb{R}^{H\times W\times3} x∈RH×W×3 ,先利用一个编码器 E E E来将图像编码到潜在表示空间 z = E ( x ) z={\mathcal{E}}(x) z=E(x),其中 z ∈ R h × s × c z \in \mathbb{R}^{h \times s \times c} z∈Rh×s×c,然后用解码器从潜在表示空间重建图片 x ~ = D ( z ) = D ( E ( x ) ) {\tilde{x}}={\mathcal{D}}(z)={\mathcal{D}}({\mathcal{E}}(x)) x~=D(z)=D(E(x)) 。在感知压缩压缩的过程中,下采样因子的大小为 f = H / h = W / w f=H/h=W/w f=H/h=W/w,它是2的次方,即 f = 2 m f=2^{m} f=2m 。
2.1.3 训练
在训练autoencoder过程中,除了采用L1重建损失外,还增加了感知损失(perceptual loss,即LPIPS,具体见论文The Unreasonable Effectiveness of Deep Features as a Perceptual Metric)以及基于patch的对抗训练。同时为了防止得到的latent的标准差过大,采用了两种正则化方法:第一种是KL-reg,类似VAE增加一个latent和标准正态分布的KL loss,这里为了保证重建效果,采用比较小的权重(~10e-6);第二种是VQ-reg,引入一个VQ (vector quantization)layer,此时的模型可以看成是一个VQ-GAN,不过VQ层是在decoder模块中,这里VQ的codebook采样较高的维度(8192)来降低正则化对重建效果的影响.具体损失函数如下所示:
L A u t o e n c o d e r = min ε , D max ψ ( L r e c ( x , D ( E ( x ) ) ) − L a d v ( D ( E ( x ) ) ) + log D ψ ( x ) + L r e g ( x ; E , D ) ) {\cal L}_{\mathrm{Autoencoder}}=\operatorname*{min}_{\varepsilon,D}\operatorname*{max}_{\psi}\left({\cal L}_{r e c}(x,{\cal D}({\cal E}(x)))-{\cal L}_{a d v}({\cal D}({\cal E}(x)))+\log{\cal D}_{\psi}(x)+{\cal L}_{r e g}(x;{\cal E},{\cal D})\right) LAutoencoder=ε,Dminψmax(Lrec(x,D(E(x)))−Ladv(D(E(x)))+logDψ(x)+Lreg(x;E,D))
上式摘自论文的附录,但是该损失与论文3.1章节描述有出入,3.1中描述还有感知损失,然而此处并没有;此外,该损失函数中对抗损失的写法貌似也不太正确。总而言之,在训练Autoencoder过程中包含如下几个损失:
- 重建损失(Reconstruction Loss):是重建图像与原始图像在像素空间上的均方误差
- 感知损失(Perceptual Loss):是最小化重构图像和原始图像分别在预训练的VGG网络上提取的特征在像素空间上的均方误差;可参考感知损失(perceptual loss)详解
- 对抗损失(Adversarial Loss):使用Patch-GAN的判别器来进行对抗训练, 可参考PatchGAN原理
- 正则项(KL divergence Loss):通过增加正则项来使得latent的方差较小且是以0为均值,即计算latent和标准正态分布的KL损失
论文将不同的autoencoder在扩散模型上进行实验,在ImageNet数据集上训练同样的步数(2M steps),其训练过程的生成质量如下所示,可以看到过小的(比如1和2)下收敛速度慢,此时图像的感知压缩率较小,扩散模型需要较长的学习;而过大的其生成质量较差,此时压缩损失过大。
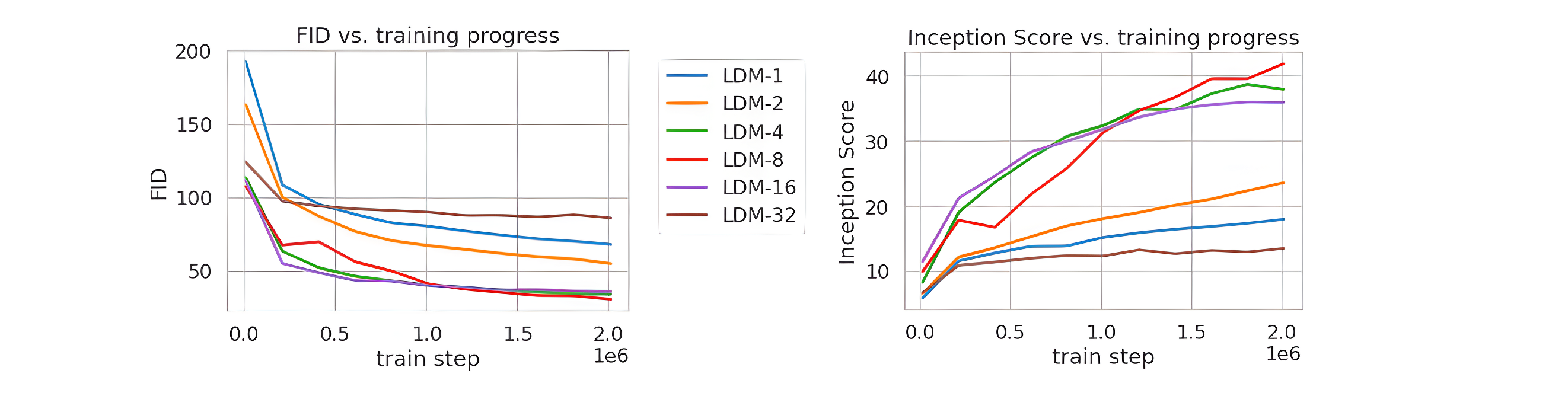
当 f f f 在4~16时,可以取得相对好的效果。SD采用基于KL-reg的autoencoder,其中下采样率 f = 8 f=8 f=8,特征维度为 c = 4 c=4 c=4,当输入图像为512x512大小时将得到64x64x4大小的latent。
autoencoder将图片压缩到latent后再重建其实是有损的,比如会出现文字和人脸的畸变等情况,这种有损压缩对SD的生成图像质量是有一定影响的。此外,由于KL-reg的权重系数非常小,实际得到latent的标准差还是比较大,latent diffusion论文中提出了一种rescaling方法:首先计算出第一个batch数据中的latent的标准差 δ ^ \hat \delta δ^,然后采用 1 / δ ^ 1/\hat \delta 1/δ^这个系数来rescale latent,这样就尽量保证latent的标准差接近1(防止扩散过程的SNR较高,影响生成效果),然后扩散模型也是应用在rescaling的latent上,在解码时只需要将生成的latent除以 1 / δ ^ 1/\hat \delta 1/δ^,然后再送入autoencoder的decoder即可。对于SD 1.x所使用的autoencoder,这个rescaling系数为0.18215。
2.2 潜在扩散模型(Latent Diffusion Models)
SD中的扩散模型结构与1.6章节中图类似,主要差别在于增加了CrossAttention来引入条件,Attention的query是UNet的中间特征,而key和value则是text embeddings。将AutoEncoder的编码器输出的latent加噪后作为Unet的输入(同时还有其他条件输入),来预测噪声, 损失函数就是真实噪声和预测噪声的L1或L2损失。
在训练条件扩散模型时,会采用Classifier-Free Guidance (简称为CFG),即在训练条件扩散模型的同时也训练一个无条件的扩散模型,将条件控制下预测的噪音和无条件下的预测噪音组合在一起来确定最终的噪音,具体的计算公式如下所示
pred_noise = w ⋅ cond_pred_noise + ( 1 − w ) ⋅ uncond_pred_noise = w ϵ θ ( x t , t , c ) + ( 1 − w ) ϵ θ ( x t , t ) \begin{aligned} \text {pred\_noise} & =w \cdot \text {cond\_pred\_noise}+(1-w) \cdot \text {uncond\_pred\_noise} \\ & =w \epsilon_\theta\left(\mathbf{x}_t, t, \mathbf{c}\right)+(1-w) \epsilon_\theta\left(\mathbf{x}_t, t\right) \end{aligned} pred_noise=w⋅cond_pred_noise+(1−w)⋅uncond_pred_noise=wϵθ(xt,t,c)+(1−w)ϵθ(xt,t)
这里的 w w w为guidance scale,当 w w w越大时,condition起的作用越大,即生成的图像其更和输入文本一致。CFG的具体实现非常简单,在训练过程中,我们只需要以一定的概率(比如10%)随机drop掉text即可,将text置为空字符串;SD默认采用的guidance_scale为7.5,当guidance_scale较低时生成的图像效果是比较差,当采用更大的guidance_scale比如11,图像的色彩过饱和而看起来不自然。
此外CFG和SD的negtive prompt参数相关,在去噪过程时的噪音预测不仅仅依赖条件扩散模型,也依赖无条件扩散模型:这里的negative_prompt便是无条件扩散模型的text输入,上面说过训练过程中我们将text置为空字符串来实现无条件扩散模型,即negative_prompt = None = “”。但是有时候我们可以使用不为空的negative_prompt来避免模型生成的图像包含不想要的东西,因为从上述公式可以看到这里的无条件扩散模型是我们想远离的部分。
最后,SD默认生成512x512大小的图像,但实际上可以生成其它分辨率的图像,但是可能会出现不协调,如果采用多尺度策略训练,会改善这种情况,比如SDXL。
2.3 条件机制(Conditioning Mechanisms)
SD采用CLIP text encoder来对输入text 提取text embeddings,具体的是采用目前OpenAI所开源的最大CLIP模型:clip-vit-large-patch14。对于输入text,送入CLIP text encoder后得到最后的hidden states,其特征维度大小为77x768(77是token的数量),这个细粒度的text embeddings将以cross attention的方式送入UNet中。注意,在训练SD的过程中,CLIP text encoder模型是冻结的。此外输入的条件不只能是文本,还可以是轮廓图,图片等。
2.4 模型测评
对于文生图模型,目前常采用的定量指标是FID(Fréchet inception distance)和CLIP score,其中FID可以衡量生成图像的逼真度(image fidelity),而CLIP score评测的是生成的图像与输入文本的一致性,其中FID越低越好,而CLIP score是越大越好。当CFG的gudiance scale参数设置不同时,FID和CLIP score会发生变化,下图为不同的gudiance scale参数下,SD模型在COCO2017验证集上的评测结果,注意这里是zero-shot评测,即SD模型并没有在COCO训练数据集上精调。
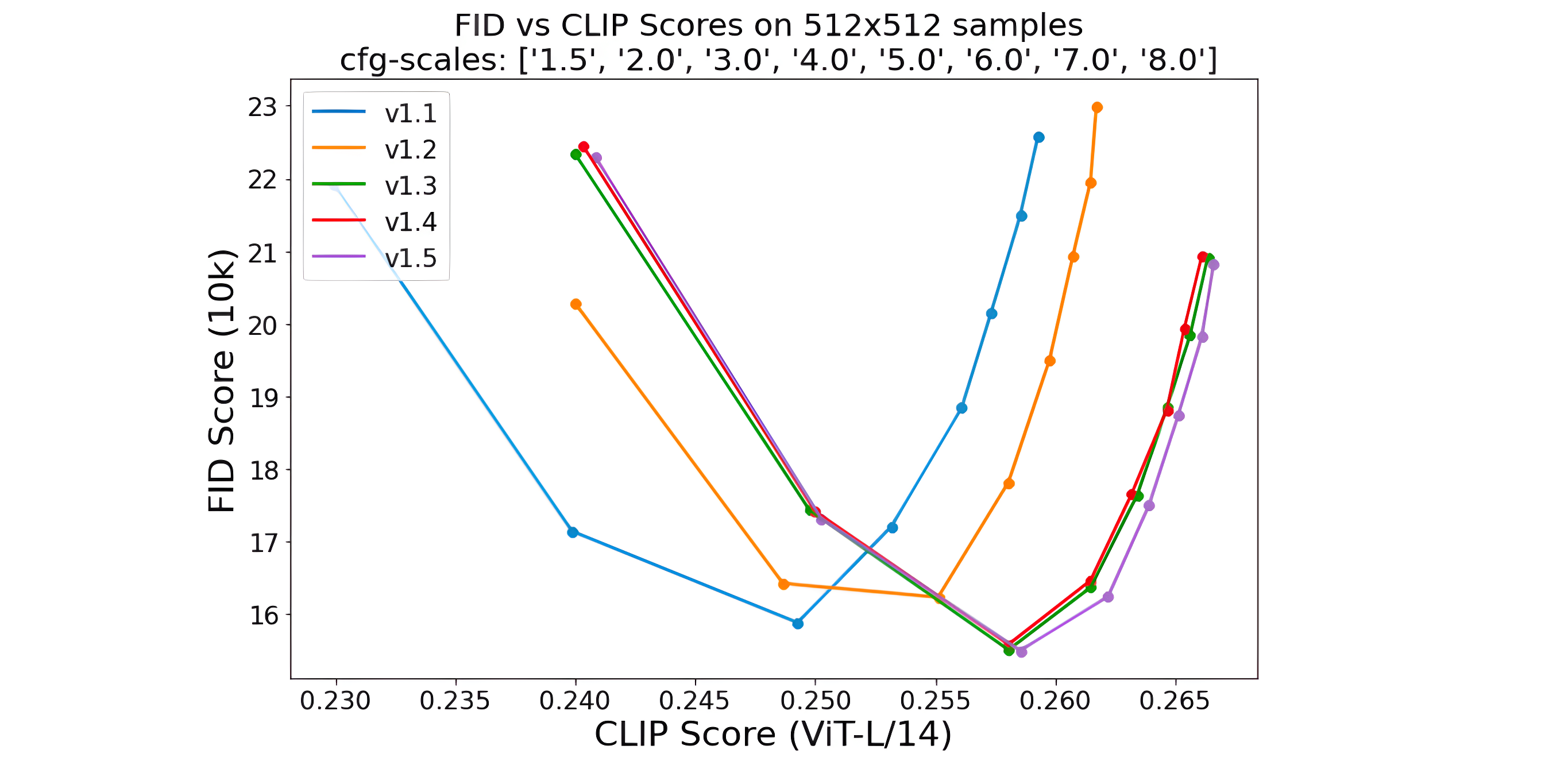
2.5 小结
本章节主要对SD的结构进行了讲解,但是部分细节并没有涉及,比如CrossAttention是如何交互的。此外对于SD的具体应用,如文生图、图生图、Inpainting等操作都未讲解,这些细节都将在下一篇文章和代码结合在一起讲解。
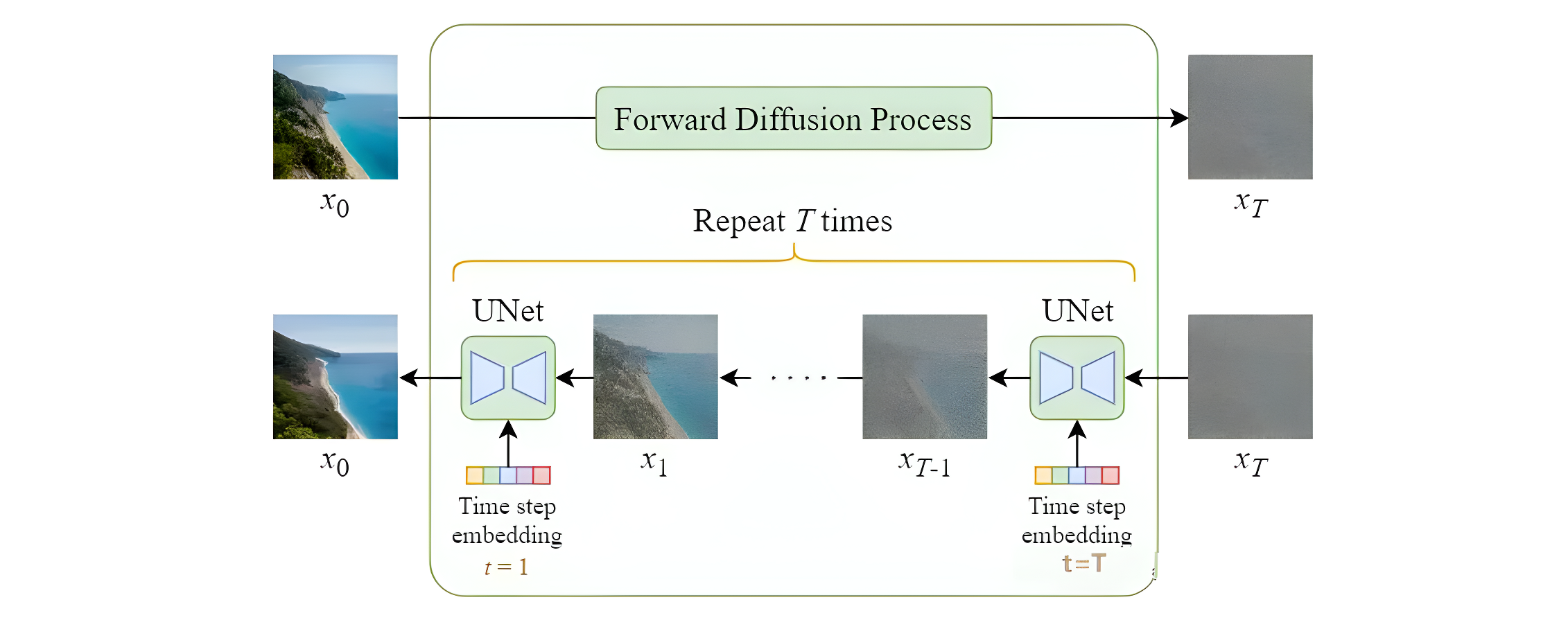
下面两张图片分别展示了普通扩散模型和Stable Diffusion的模型结构对比,可以看到最大的区别在于SD使用了自编码器将原始图片进行了压缩,从而有利于减少计算资源,以及SD引入了contition模块,从而使得文生图等得以实现。
3. 参考
- 深入浅出扩散模型系列:基石DDPM(模型架构篇),最详细的DDPM架构图解 👍
- 彻底搞懂CNN中的卷积和反卷积
- Diffusion 和Stable Diffusion的数学和工作原理详细解释
- Stable Diffusion原理解读
- 一文看懂PatchGAN
- Understanding Stable Diffusion
- 感知损失(perceptual loss)详解
- 硬核解读Stable Diffusion(完整版)👍
- stabel diffusion 代码库
- diffusers 代码库
- High-Resolution Image Synthesis with Latent Diffusion Models
- runwayml/stable-diffusion-v1-5