传送门
题目大意
- 依次给定\(n\)个区间,并给定\(q\)个数,每个数依次经过这些区间时若在区间中则加1,问最后每个数变成了多少。
做法
- 显然如果直接模拟的话时间复杂度肯定是会炸的。
- 首先我们注意到这道题是可以离线处理的,并且对于所有询问的数,我们如果先对他们排好序,在每个数都各自依次经过所给的区间之后,最后的序列依然是非递减的(可以自己试着感性证明一下),于是问题就变成了:依次对于所给的区间,在一个有序的数列当中找到所有属于这个区间的数,并使他们加1。而所有属于这个区间的数在这个数列中一定是连续的(因为这个数列是非递减的),那么就引申出了做法。
- 首先提供一种树状数组的思路,我们可以用二分来找到当前这个数列中第一个小于当前区间左端点\(l[i]\)的数的位置和第一个大于当前区间右端点\(r[i]\)的数的位置,然后利用差分进行每次的修改。由于在二分的过程中对于每个数的判断都需要树状数组求差分前缀和,所以时间复杂度是\(O(nlog^{2}n)\)的。
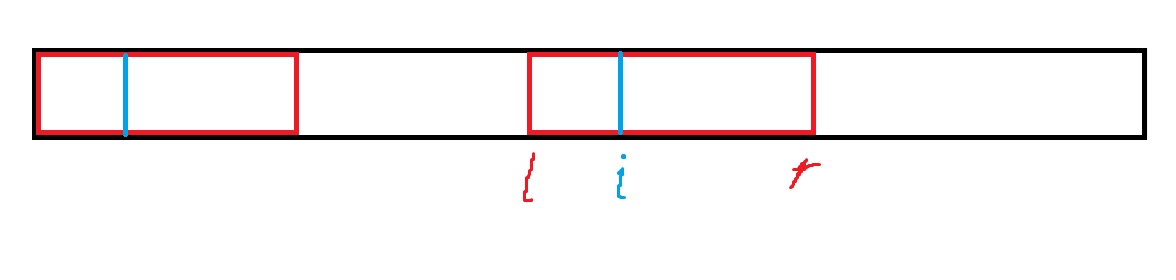
- 再给出一种线段树二分的做法。我们可以利用线段树来维护所给的询问排好序后的数列中最小值和最大值,在每次区间修改操作时,对于当前区间,如果当前区间最小值不比\(l[i]\)小,最大值不比\(r[i]\)大,那么当前区间肯定是需要直接全部加1的。而对于其他情况,线段树中当前区间的左儿子区间的数一定是比右儿子区间的数小的,所以如果\(l[i]\)比左儿子区间的最大值小那么说明左儿子区间存在需要修改的值,如果\(r[i]\)比右儿子区间的最小值大那么说明右儿子区间存在需要修改的值,再往后递归即可。
- 最后就是数组一定不要开小了
代码
#include<bits/stdc++.h>using namespace std;long long t;
const long long N = 5e5 + 10;
long long n,q;
long long l[N],r[N],add[3000010],minv[3000010],maxn[3000010];
long long ans[600010],p[3000010];
struct node {long long num,pos;bool operator < (const node &a) const {return num < a.num;}
}query[600010];void build(long long k,long long l,long long r) {if(l == r) {minv[k] = maxn[k] = query[l].num;p[k] = query[l].pos;return;}long long mid = (l + r) >> 1;build(k * 2,l,mid);build(k * 2 + 1,mid + 1,r);minv[k] = min(minv[k * 2],minv[k * 2 + 1]);maxn[k] = max(maxn[k * 2],maxn[k * 2 + 1]);
}void Add(long long k,long long l,long long r,long long v) {minv[k] += v;maxn[k] += v;add[k] += v;
}void pushdown(long long k,long long l,long long r,long long mid) {Add(k * 2,l,mid,add[k]);Add(k * 2 + 1,mid + 1,r,add[k]);add[k] = 0;
}void modify(long long k,long long l,long long r,long long x,long long y) {if(l == r) {if(minv[k] >= x && maxn[k] <= y) minv[k]++,maxn[k]++;return;}if(x <= minv[k] && maxn[k] <= y) {minv[k]++;maxn[k]++;add[k]++;return ;}long long mid = (l + r) >> 1;pushdown(k,l,r,mid);if(x <= maxn[k * 2]) modify(k * 2,l,mid,x,y);if(y >= minv[k * 2 + 1]) modify(k * 2 + 1,mid + 1,r,x,y);minv[k] = min(minv[k * 2],minv[k * 2 + 1]);maxn[k] = max(maxn[k * 2],maxn[k * 2 + 1]);
}void rbuild(long long k,long long l,long long r) {if(l == r) {ans[p[k]] = maxn[k];return;}long long mid = (l + r) >> 1;pushdown(k,l,r,mid);rbuild(k * 2,l,mid);rbuild(k * 2 + 1,mid + 1,r);
}void solve() {cin >> n;for(long long i = 1;i <= n;i++) cin >> l[i] >> r[i];cin >> q;for(long long i = 1;i <= q;i++) {cin >> query[i].num;query[i].pos = i;}sort(query+1,query+1+q);build(1,1,q);for(long long i = 1;i <= n;i++)modify(1,1,q,l[i],r[i]);rbuild(1,1,q);for(long long i = 1;i <= q;i++) cout << ans[i] << '\n';
}signed main() {ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);t = 1;while(t--) solve();return 0;
}