时间序列平稳性的双重假设检验：KPSS与ADF方法比较研究

在进行时间序列分析之前，确定序列的平稳性是一个关键步骤。平稳性指的是时间序列的统计特性（如均值和方差）在时间维度上保持不变。本文将详细介绍如何运用 KPSS 检验和 Dickey-Fuller 检验来验证序列的平稳性。这两种检验方法基于不同的统计假设：KPSS 检验的原假设是数据非平稳，而 Dickey-Fuller 检验则假设数据平稳。

时间序列平稳性的基本概念

时间序列的平稳性主要体现在三个方面：

1. 均值稳定性：序列的期望值在时间维度上保持恒定
2. 方差稳定性：数据波动范围保持相对稳定
3. 无周期性：数据不存在明显的周期性波动或循环模式

平稳性是许多时间序列模型（如 ARIMA）的基本假设条件，对模型的有效性具有重要影响。

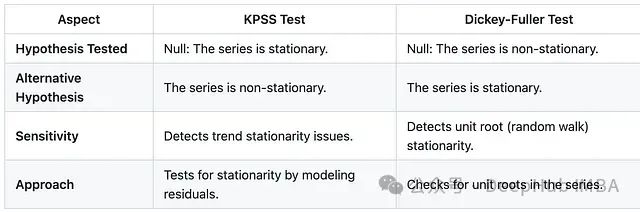
以下我们将通过构造平稳序列和非平稳序列来演示这两种检验方法的应用。

 

https://avoid.overfit.cn/post/be3a54e988ff4970a54584dbbf6ec2e5