卡特兰数
定义
\(Catalan\) 数列 \(H_n\) 是以下问题的方案数:
- 有一个大小为 \(n × n\) 的方格图,左下角为 \((0, 0)\) 右上角为 \((n, n)\),从左下角开始 每次都只能向右或者向上走一单位,不走到对角线 \(y = x\) 上方(但可以触碰) 的情况下到达右上角有多少可能的路径?
- 在圆上选择 \(2n\) 个点,将这些点成对连接起来使得所得到的 \(n\) 条线段不相交的 方法数?
- 一个栈的进栈序列为 \(1, 2, 3, · · · , n\) 有多少个不同的出栈序列?
- \(n\) 个结点可构造多少个不同的二叉树?
- \(n\) 对括号能组成的括号序列数?
- ......
这些问题的方案数可以证明是相等的。我们先以第一个命题来具体研究 \(Catalan\) 数
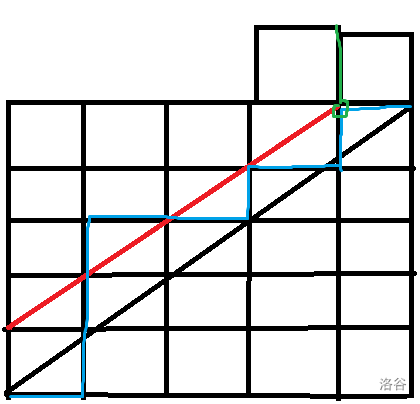
图片有点抽象还请各位海涵一下。
我们从(1,1)走到(n,n)的方案数可以递推来求。
设我们第一次接触到对角线时的横坐标为i,前面的方案数可看为从(2,1)走到(i,i-1)的方案数,后面的方案数可看为从(i,i)走到(n,n)的方案数。
对 i 求和有:\(H_n = \sum^{n}_{i=1}H_{i-1}H_{n-i}\),这就是卡特兰数的递推式。初值为 \(H_0 = H_1 = 1\)。
我们还可以看为总方案数减去超过对角线(触碰到红线)的方案数。
我们对最后一次触碰到红线后的部分进行翻转,则原来的每一条不合法路径(如蓝色)就一一对应了一条终点为(n-1,n+1)的路径(如绿色)。
所以卡特兰数的组合意义是 \(H_n = {2n \choose n} - {2n \choose n-1}\)。
综上:
再看卡特兰数的第二个和第四个定义,可以发现它们的递推式与该递推式相同。对于第三个和第五个定义,可以认为就是在走网格,并且横向步数不超过纵向步数。
通项公式:\(H_n = \frac{\binom{2n}{n}}{n + 1}\)。这个使用递推公式的生成函数搞出来的,证明比较麻烦,这里不再赘述 。你也可以把该式子带入组合意义中来验证其正确性。
递推式2:\(H_n = \frac{H_{n - 1}(4n - 2)}{n + 1}\) ,这个可以直接带入验证。
因为上课讲的例题都没怎么听懂,这里就不放题了。


![[CF1260D] A Game with Traps](https://cdn.luogu.com.cn/upload/image_hosting/95wguc7s.png)


