集训2 20240124

集训2 20240124

牛客竞赛_ACM/NOI/CSP/CCPC/ICPC算法编程高难度练习赛_牛客竞赛OJ

A：

题目大意：给出 \(7\) 个数，判断有没有 \(4,7\)

#include<bits/stdc++.h>using namespace std;int main()
{int a[7];for (int i=0;i<7;i++) cin>>a[i];for (int i=0;i<7;i++){if (a[i]==4||a[i]==7){cout<<"NO";return 0;}}cout<<"YES";return 0;
}

签到题还罚了两发，服了

B：

题目大意：给定一个数组，输出一个数，这个数至少要比数组中一半的数要小，给出最大的取值

#include<bits/stdc++.h>using namespace std;int a[500010];int main()
{int n;cin>>n;for (int i=1;i<=n;i++) cin>>a[i];sort(a+1,a+n+1);cout<<a[n/2+1]-1;return 0;
}

输入排序后找中位数，\(n\) 为偶数时，输出较大的数

F：

题目大意：在给定的区间 \([l,r]\) 内取两个整数 \(x,y\)，满足 \(x+y=x\ {\rm{xor}}\ y+x\ {\rm{and}}\ y+x\ {\rm{or}}\ y\)

#include<bits/stdc++.h>using namespace std;void solve(void){long long l,r;cin>>l>>r;cout<<r-l+1<<endl;return;
}int main()
{int T;cin>>T;while(T--)solve();return 0;
}

乱猜的结论，当且仅当 \(x=y\) 时，等式成立

证明如下：

设 \(x,y\) 二进制下的第 \(i\) 位为 \(\overline{x},\overline{y}\)，有以下情况

• \(\overline{x}=1,\overline{y}=1\)：\(\overline{x}\ {\rm{xor}}\ \overline{y}=0,\overline{x}\ {\rm{and}}\ \overline{y}=1,\overline{x}\ {\rm{or}}\ \overline{y}=1,\overline{x}\ + \overline{y}=10\)

• \(\overline{x}=1,\overline{y}=0\)：\(\overline{x}\ {\rm{xor}}\ \overline{y}=1,\overline{x}\ {\rm{and}}\ \overline{y}=0,\overline{x}\ {\rm{or}}\ \overline{y}=1,\overline{x}\ + \overline{y}=1\)（\(\overline{x}=0,\overline{y}=1\) 同理）

• \(\overline{x}=0,\overline{y}=0\)：\(\overline{x}\ {\rm{xor}}\ \overline{y}=0,\overline{x}\ {\rm{and}}\ \overline{y}=0,\overline{x}\ {\rm{or}}\ \overline{y}=0,\overline{x}\ + \overline{y}=0\)

不难发现，\(x+y=x\ {\rm{and}}\ y+x\ {\rm{or}}\ y\)，所以等式可以转化为

\[x+y=x\ {\rm{xor}}\ y+x\ {\rm{and}}\ y+x\ {\rm{or}}\ y\iff x\ {\rm{xor}}\ y=0 \]

\(x=y\) 时等式显然成立，得证

G：

题目大意：给定 \(n,m\)，每次操作可以使 \(m\) 扩大 \(m\) 倍，求至少多少次操作后 \(m\) 最接近 \(n\)

#include<bits/stdc++.h>using namespace std;void solve(void){long long n,m;cin>>n>>m;if (m==1||n<m){cout<<1<<endl;return;}int ex=log(n)/log(m);if (n-pow(m,ex)>pow(m,ex+1)-n){cout<<ex+1<<endl;}else{cout<<ex<<endl;}
}int main()
{int T;cin>>T;while(T--)solve();return 0;
}

假设操作次数为 \(k\) ，那么满足 \(m^{k}\le n\le m^{k+1}\)

题目可以转化为求解函数

\[ans= \begin{cases} \lfloor\log_mn\rfloor &&\text{$n-m^k<m^{k+1}-n$}\\ \\\lfloor\log_mn\rfloor+1 &&\text{$n-m^k\ge m^{k+1}-n$} \end{cases}\quad (k=\lfloor\log_mn\rfloor) \]

注意特判 \(m=1\) 与 \(n<m\) 的情况，他们的结果都为 \(1\)，题目要求最开始需要一个 \(m\)

J：

题目大意：根据时间判断在不同时间段内的人数（同一编号算一个人）

#include<bits/stdc++.h>using namespace std;set<string> pa,pb,pc;int main()
{int n,h,m;cin>>n>>h>>m;int a=0,b=0,c=0;for (int i=1;i<=n;i++){string num;cin>>num;int yy,MM,dd,hh,mm,ss;scanf(" %d-%d-%d %d:%d:%d",&yy,&MM,&dd,&hh,&mm,&ss);if (yy==h&&MM==m){if ((hh>=7&&(hh<9||(hh==9&&mm==0&&ss==0)))||(hh>=18&&(hh<20||(hh==20&&mm==0&&ss==0)))) {if (!pa.count(num)){a++;pa.insert(num);}}if ((hh>=11&&(hh<13||(hh==13&&mm==0&&ss==0)))){if (!pb.count(num)){b++;pb.insert(num);}}if ((hh>=22&&hh<=23)||(hh>=0&&(hh<1|| (hh==1&&mm==0&&ss==0)))){if (!pc.count(num)){c++;pc.insert(num);}}}}cout<<a<<' '<<b<<' '<<c;return 0;
}

乱模拟就行，一个人在相同时间段内的记录不能重复计数，所以用 set 存人的编号

K：

题目大意：

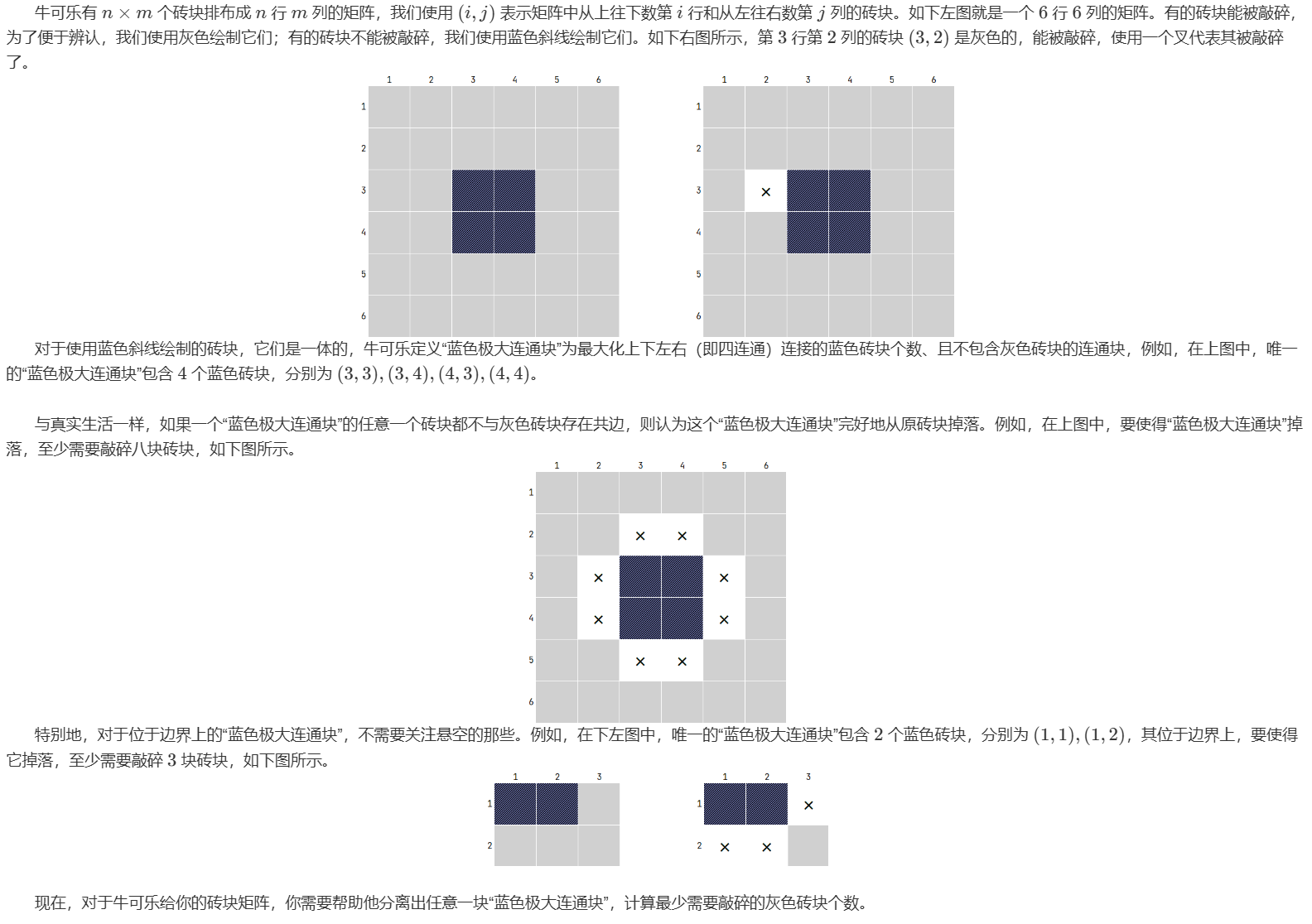
#include<bits/stdc++.h>using namespace std;char mp[505][505];
int ans=1e9;
int dx[]={1,0,-1,0};
int dy[]={0,1,0,-1};void bfs(int x,int y){bool vis[505][505]={0};int sum=0;queue<pair<int,int>> q;q.push({x,y});while(q.size()){auto t=q.front();q.pop();for (int i=0;i<4;i++){int tx=t.first+dx[i],ty=t.second+dy[i];if(mp[tx][ty]=='1'){//如果下一个位置是1，可以连通过去mp[tx][ty]='2';//立刻标记为2，已经跑过了，防止多次入队！！！q.push({tx,ty});//入队}if(mp[tx][ty]=='0'&&vis[tx][ty]==0){//如果是灰砖，就需要敲碎sum++;//计数vis[tx][ty]=1;//标记敲碎的灰砖}}}ans=min(ans,sum);//更新答案
}int main()
{int n,m;cin>>n>>m;for (int i=0;i<=n+1;i++){for (int j=0;j<=m+1;j++){if ((i==0||i==n+1)||(j==0||j==m+1))mp[i][j]='9';//标记边界elsecin>>mp[i][j];}}for (int i=1;i<=n;i++){for (int j=1;j<=m;j++){if (mp[i][j]=='1'){//只对1进行bfsbfs(i,j);}}}cout<<ans;return 0;
}

存图，跑一遍 bfs，每次开一个状态图，用来存使当前连通块掉落的灰色砖块的位置（因为每次bfs时连通块都是相互独立的）

对跑过 bfs的连通块都做标记，下次遍历到时就跳过

D：

题目大意：给定一个字符串，这个字符串存在长 \(k\) 的连续子串 \(a\) ，和长 \(k\) 的不连续子串 \(b\)，求满足 \(a=b\) 的最大 \(k\) 值

• 子串不能为空

• 不连续子串至少由两段不相邻的子串构成

#include<bits/stdc++.h>using namespace std;char c[200010];
int st[30];int main()
{    int n;cin>>n;int ans=0;for (int i=1;i<=n;i++){cin>>c[i];if (st[c[i]-'a'])//找独立元素bans=max(st[c[i]-'a'],ans);st[c[i]-'a']=i;}memset(st,0,sizeof st);for (int i=n;i>=1;i--){if (st[c[i]-'a'])//找独立元素aans=max(st[c[i]-'a'],ans);st[c[i]-'a']=n-i+1;}cout<<(ans==1?0:ans);return 0;
}

不连续子串最优的情况是一个独立元素加一个连续子串

可以分为两种状况讨论：\(a[n]+b\) 和 \(a+b[n]\)，设选取的连续子串为 \(s_{i,j}\)，那么 \(a[n],b[n]\) 就在 \(s_{i,j}\) 内

对应的独立元素 \(b,a\) 就需要在 \(j\) 之后与 \(i\) 之前找

特别的，对于类似 aba 这样的字符串，需要特判一遍答案为 \(0\)

H：

题目大意：给定一个矩形，矩形边上的三个点确定的圆半径最大时，三个点的坐标

#include<bits/stdc++.h>using namespace std;void solve(void){int a,b,c,d;cin>>a>>b>>c>>d;if (b-a>d-c){cout<<a<<' '<<d-1<<endl;cout<<b<<' '<<d<<endl;;cout<<b-1<<' '<<d<<endl;}else{cout<<a<<' '<<c<<endl;;cout<<a+1<<' '<<d<<endl;;cout<<a<<' '<<c+1<<endl;}
}int main()
{int T;cin>>T;while(T--)solve();return 0;
}

数学知识，三个点可以确定一段弧，这段弧的曲率越小，曲率半径就越大，由于题目要求的点都为整数点

所以使这三个在矩形上的点确定的弧越像直线，那么确定的圆的半径就越大

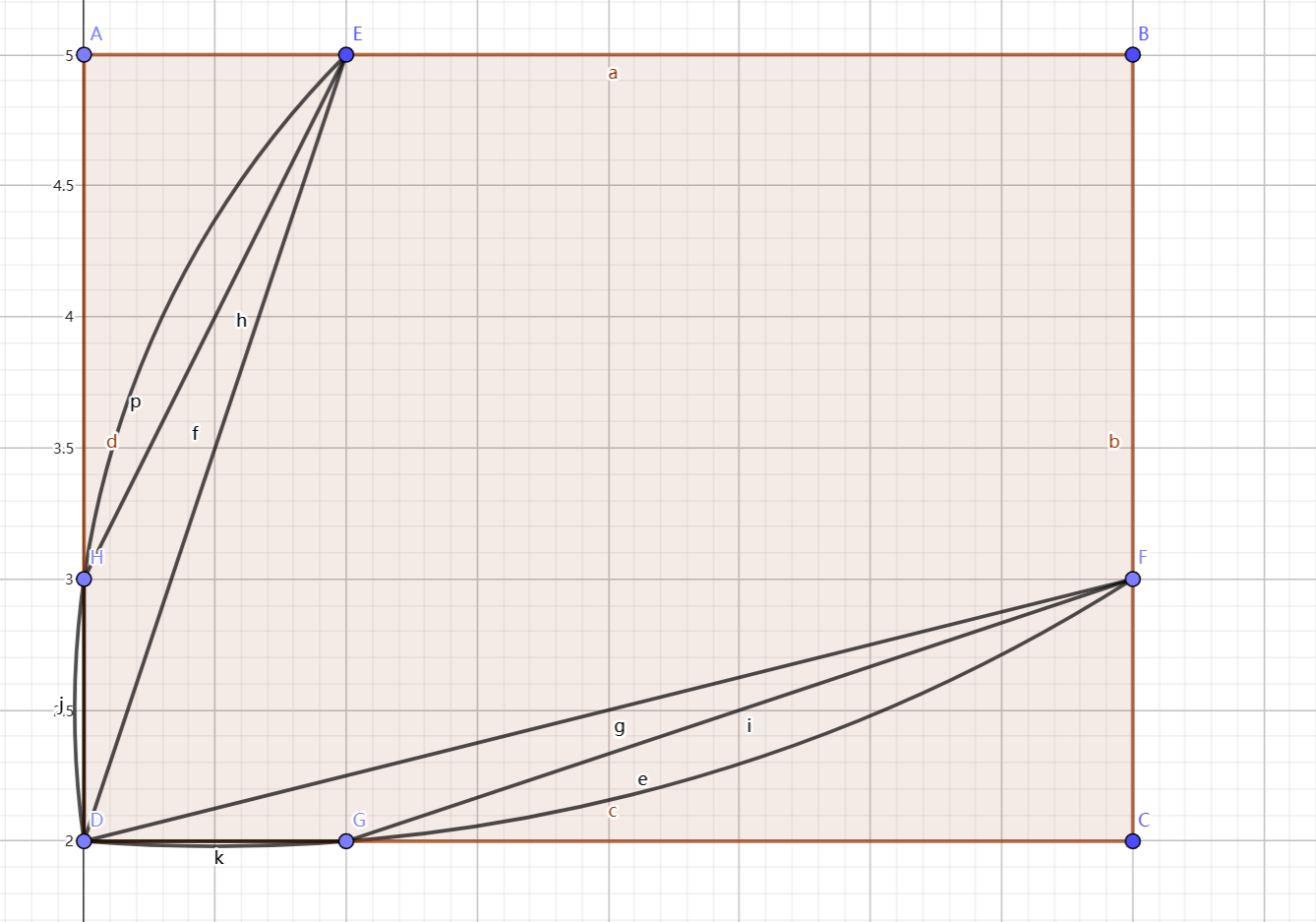
可以看出，优先确定两个在长边上的点与一个在短边上的点，构成的圆弧曲率越小，即这三个点最接近一条直线

那么答案就能显然得到了

C：

题目大意：给出 \(n,m\) ，构造一个长 \(n\) 的字符串，使它的可爱度为 \(m\)，可爱度定义参考：这个字符串存在长 \(k\) 的连续子串 \(a\) ，和长 \(k\) 的不连续子串 \(b\)，满足 \(a=b\) 的最大 \(k\) 值

#include<bits/stdc++.h>using namespace std;void solve(void){int n,m;cin>>n>>m;if (n==m||n-m>26){cout<<"NO"<<endl;return ;}elsecout<<"YES"<<endl;for (int i=0;i<n;i++){cout<<(char)('a'+i%(n-m));}cout<<endl;
}int main()
{int T;cin>>T;while (T--)solve();return 0;
}

根据 D 可以知道可爱度只和最后一个字符以及倒数第二个这个字符的位置有关

正向考虑连续子串那么就存在：

\[\{ \overbrace{\cdots\cdots\cdots}^{m-1}\ X\ \underbrace{\cdots\cdots\cdots}_{\text{none X}}\ X \} \]

第二段省略号中不包含 \(X\) 字符且字符互不相同，所以 \(n-m>26\)（最多填充 \(25\) 个不同的字符）

考虑第一段省略号填充的内容，实际上可以填充任意的字符，因为最优解已经被确定了，即倒数第二个 \(X\) 的位置

逆向考虑连续子串：

\[\{ X\ \underbrace{\cdots\cdots\cdots}_{\text{none X}}\ X\ \overbrace{\cdots\cdots\cdots}^{m-1}\} \]

需要取逆向与正向的 \(k_{max}\) ，所以需要对称构造：

\[\{ X\ \underbrace{\cdots\cdots\cdots}_{m-1}\ \overbrace{\cdots\cdots\cdots}^{\text{none X}}\ X\ \underbrace{\cdots\cdots\cdots}_{m-1}\} \]

这样构造出来的字符串，正反来看确定可爱度的最后一个字符以及倒数第二个这个字符的相对位置没有发生改变