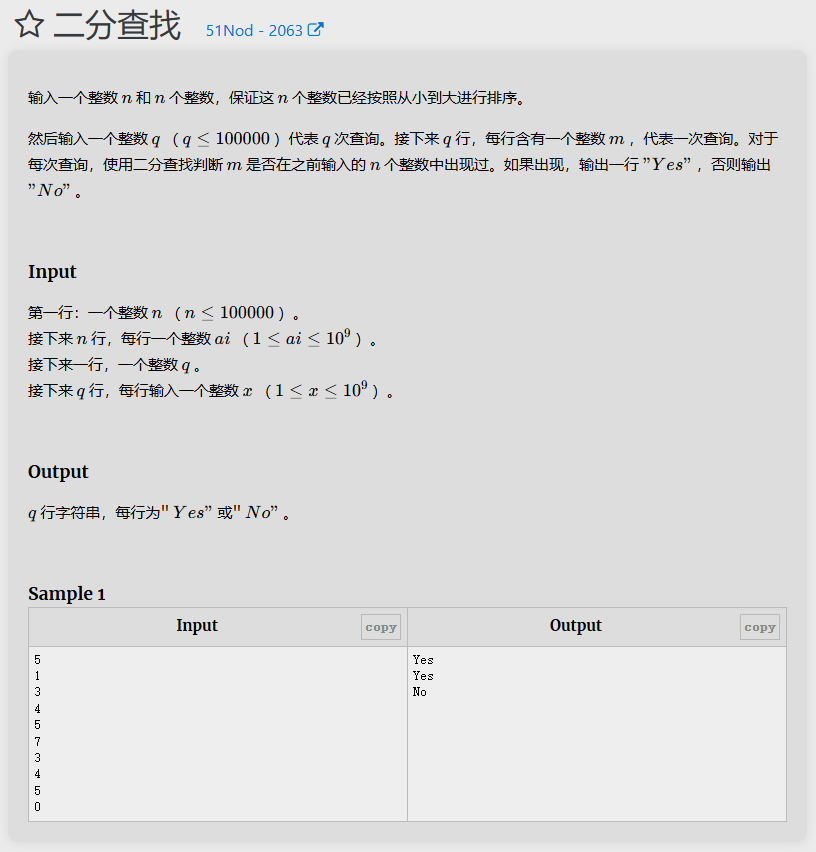
题目1
代码
#include<iostream>
#include<vector>
using namespace std;
vector<int> num;
int mybsearch(int l, int r, int x)
{while (l < r) {int mid = (l + r )>> 1;if (num[mid] >= x) r = mid;else l = mid + 1;}return l;
}
int main()
{int n,q,t;cin >> n;for (int i = 0; i < n; i++) {cin >> t;num.push_back(t);}cin >> q;for (int i = 0; i < q; i++) {cin >> t;if (t == num[mybsearch(0, n - 1, t)]) cout << "Yes" << endl;else cout << "No" << endl;}
}
解题思路
就是简单的二分查找,套模板就行。
题目2

代码
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
vector<long long> num;
long long cnt;
long long mybsearch(long long l, long long r, long long x) {while (l < r) {long long mid = (l + r )>> 1;if (num[mid] >= x) r = mid;else l = mid + 1;}return l;
}
int main()
{long long N,C,t,j,k;cin>>N>>C;for(long long i=0;i<N;i++){cin>>t;num.push_back(t);}sort(num.begin(),num.end());for(long long i=0;i<N;i++){t=num[i];t+=C;j=mybsearch(i+1,N-1,t);//while(num[j]==t){// cnt++;// j++;//}k=mybsearch(i+1,N-1,t+1);if(num[j]==t&&num[k]>t){cnt+=k-j;}else if(num[j]==t&&num[k]==t){cnt+=k-j+1;}}cout<<cnt;//cout<<mybsearch(0,N-1,4);
}
解题思路
先求B+C,再用二分法找对应位置是否有A等于B+C,找到一个后继续往后找,直到没有为止,统计数量。注意数据量大,建议都开long long。
题目3

代码
#include<iostream>
#include<vector>
using namespace std;
vector<int> H,L;
bool check(int mid,int n,int k){int cnt=0;int a,b;for(int i=1;i<=n;i++){a=H[i]/mid;b=L[i]/mid;cnt+=a*b;}if(cnt>=k) return true;else return false;
}
int work(int r,int l,int n,int k){int Ans;while(l<=r){int mid=(l+r)/2;if(check(mid,n,k)){Ans=mid;l=mid+1;}else r=mid-1;}return Ans;
}
int main()
{int N,K,a,b;int l=1,r=1e5,Ans;cin>>N>>K;H.push_back(0);L.push_back(0);for(int i=0;i<N;i++){cin>>a>>b;H.push_back(a);L.push_back(b);}Ans=work(r,l,N,K);cout<<Ans;
}
解题思路
假设切出边长为mid的正方形,设边长的范围是1到105,用二分法找出符合条件的最大的mid,保证最后切出的巧克力边长最大。
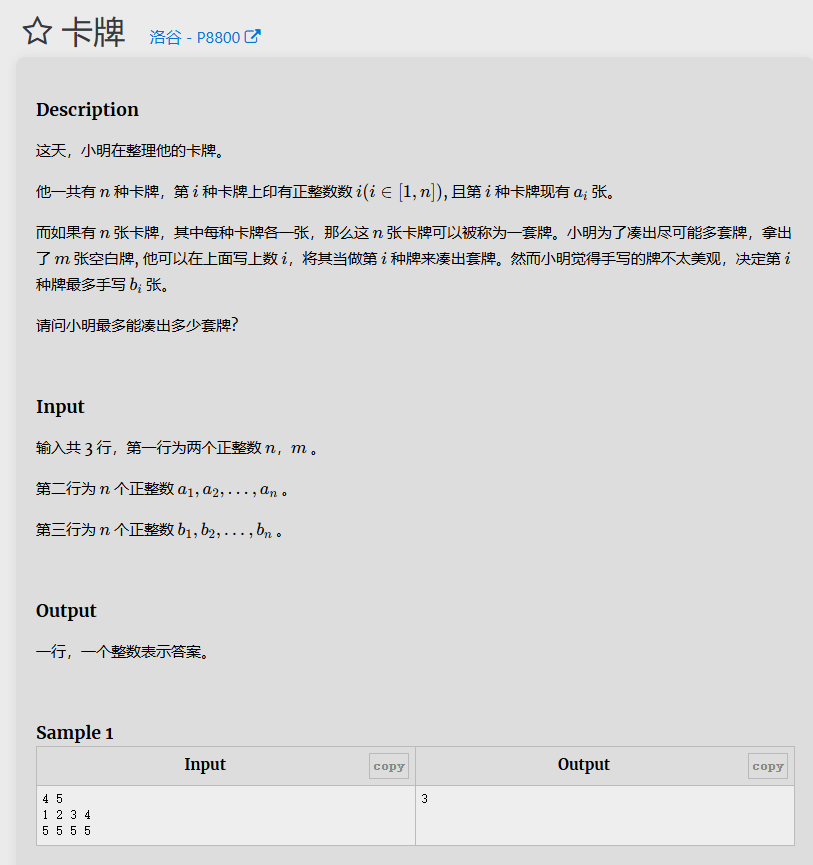
题目4
代码
#include<iostream>
#include<vector>
using namespace std;
using int64=long long;
vector<int64> a,b;
int64 n,m;
bool check(int64 mid){int64 sum=0;for(int64 i=1;i<=n;i++){if(a[i]+b[i]<mid) return false;if(a[i]<mid) sum+=mid-a[i];}if(sum<=m) return true;else return false;
}
int work(int64 l,int64 r)
{int64 Ans;while(l<=r){int64 mid=(l+r)/2;if(check(mid)){Ans=mid;l=mid+1;}else r=mid-1;}return Ans;
}
int main()
{int64 l,r,t;cin>>n>>m;a.push_back(0);b.push_back(0);l=0;r=1e10;for(int64 i=1;i<=n;i++){cin>>t;a.push_back(t);}for(int64 i=1;i<=n;i++){cin>>t;b.push_back(t);}cout<<work(l,r);
}
解题思路
找出最大值,设凑出的牌套数范围0到1010,带入mid进行二分,如果手写的牌数和原有的牌数相加都比mid小,说明这个mid太大,要排除,如果相加大于mid,说明手写的够用,手写的牌数累计到sum里,最后将sum和m进行比较,如果sum小于m,说明该方案可行,套模板最后找出最大的mid。
题目5
代码
#include<iostream>
#include<vector>
#define int long long
using namespace std;
int m,k;
int beg[1000],fin[1000],a[1000];
bool check(int mid)
{int cnt,p;cnt=1;p=mid;for(int i=1;i<=m&&cnt<=k;i++){if(a[i]>p){cnt++;i--;p=mid;}else p-=a[i];}return cnt<=k;
}
int work(int r,int l)
{int Ans=0;while(l<=r){int mid=(l+r)/2;if(check(mid)){Ans=mid;r=mid-1;}else{l=mid+1;}}return Ans;
}
signed main()
{cin>>m>>k;int l=0,r=0,t;for(int i=1;i<=m;i++){cin>>t;r+=t;a[i]=t;}l=work(r,l);fin[k]=m;beg[1]=1;for(int i=k,j=m,now=l;i>0;i--){while(now>=a[j]&&j){now-=a[j];j--;}beg[i]=j+1;fin[i-1]=j;now=l;}for(int i=1;i<=k;i++){cout<<beg[i]<<' '<<fin[i]<<'\n';}
}
解题思路
前面的人少抄写=后面的人多抄写,所以我们从最后一个人,最后一本书开始安排抄书方案,在抄写时间不超过T的情况下,令每个人抄写尽可能多的页数。这样如果存在多余的空闲时间,则会分配到前面的人上。
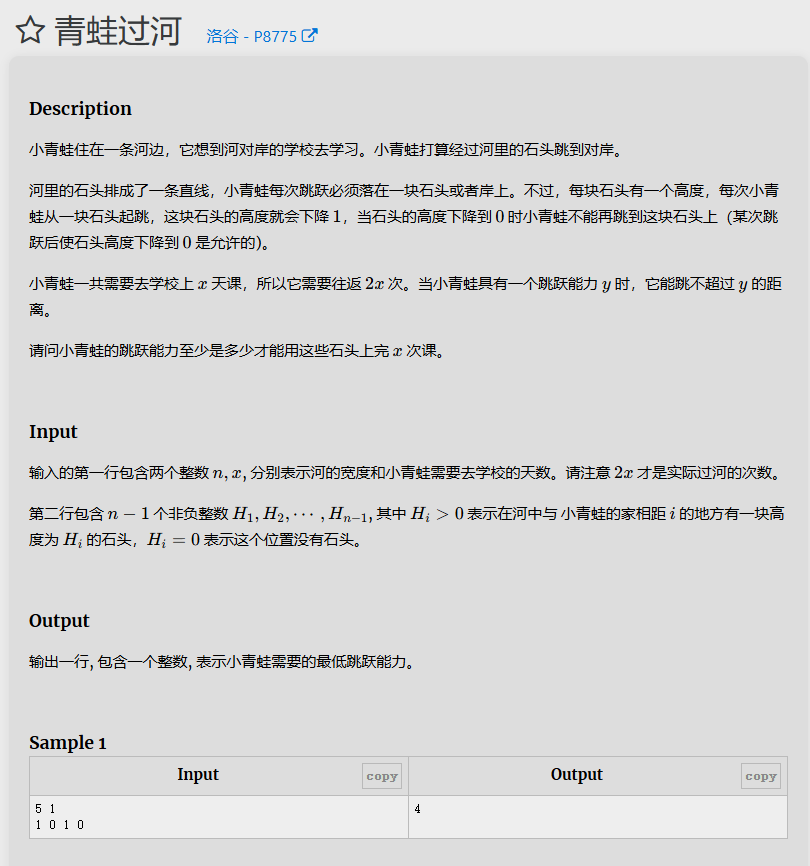
题目6
代码
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f
typedef long long LL ;
using namespace std;
const int N = 100010;
typedef pair<int ,int > PII;int n,x;
int a[N];//找到最小的y使得所有长度为y的区间和大于等于2Xint check(int y){int S = 2*x;for(int i=1; i+y-1 < n ;i++){if(a[i+y-1]-a[i-1] < S) return 0;}return 1;
}
int main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin >> n >> x;for(int i=1;i<n;i++) {cin >> a[i];a[i] += a[i-1];}int l = 0,r = N;while(l+1<r){int mid = l+r >> 1;if(check(mid)) r = mid;else l = mid ;}cout << r ; return 0;
}
解题思路
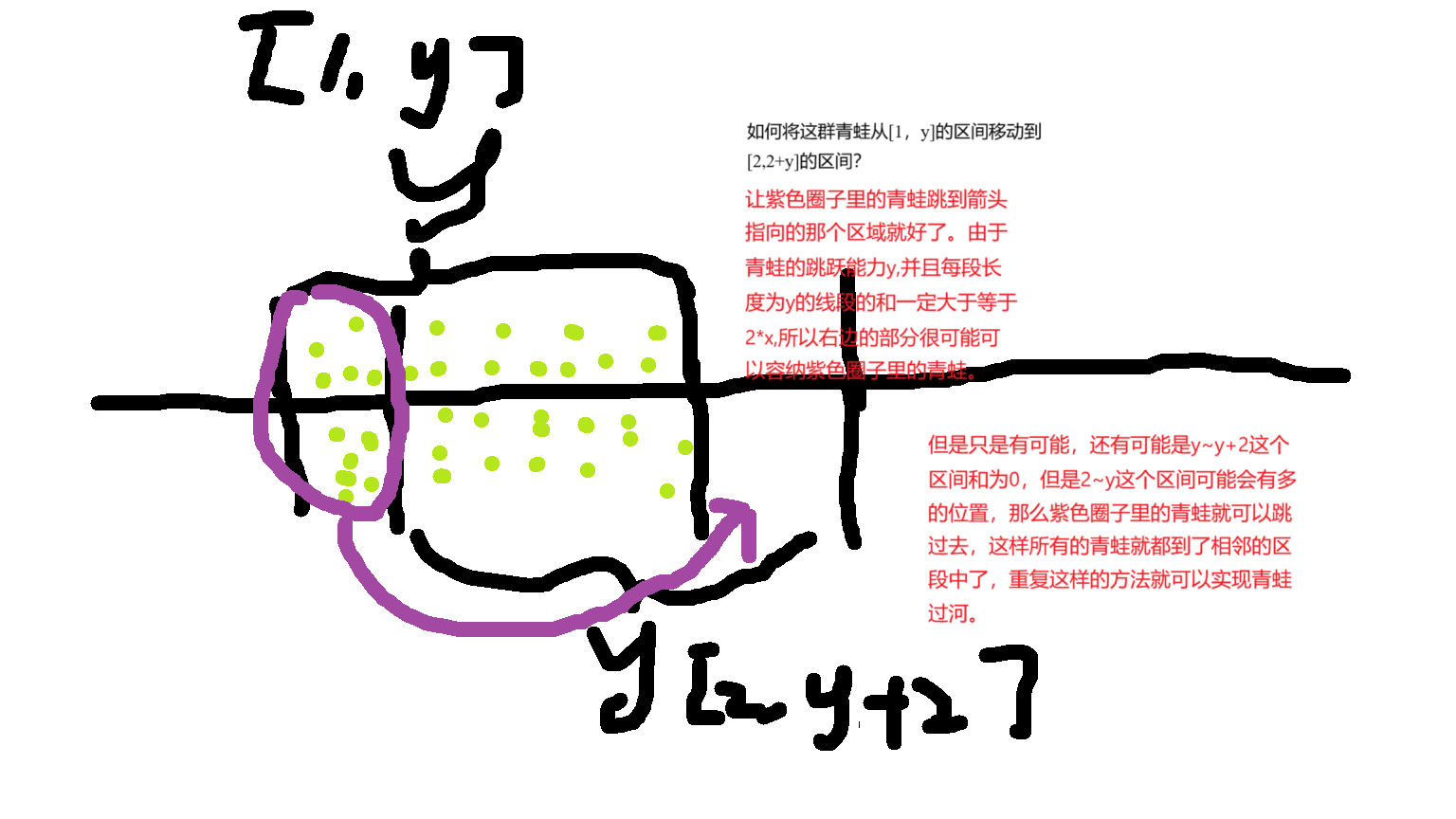
原来的一排石头可以抽象成一组数列 H。
由于小青蛙每次最多跳y个石头,所以每个长度为y连续子序列至少会被经过一次
那么 2x次路程,每个长度为y连续子序列至少会被经过2x次。所以,小青蛙能完成路程的必要条件是数列 ;中,每个长度为y连续子序列的和至少为 2x。