1.索引如何分类?
- 按照物理结构分类:①聚簇索引 ②二级索引
- 按数据结构分:①哈希表索引 ②B+树索引 ③Full-text索引
- 按字段特性分类:① 主键索引 ②唯一索引 ③普通索引 ④前缀索引
- 按照索引结构分类:①单列索引 ②联合索引
2.InnoDB的聚簇索引的默认创建机制
- 如果有主键,默认会将主键设置为聚簇索引
- 如果没有主键,InnoDB会选择第一个不含NULL且值唯一的属性作为聚簇索引
- 如果上面两个都没有的情况下,InnoDB就会生成一个隐式自增id列作为聚簇索引的索引键
3.为什么选择B+树数据结构作为索引?
①B+树 VS B树
(i)B+树种有冗余的节点,在删除节点时,无需对树的结构进行大的调整,开销较低。(ii)B+树仅有叶节点存储记录,而B树种非叶节点也要存储记录,在相同的情况下B+树对于磁盘的I/O次数更低。在用索引进行查找目标节点时,非目标节点的记录数据不仅没用,而且会花费大量的I/O时间将其读取到内存中(iii)B+树叶节点是用双向链表连接,更容易处理范围查询。、
②B+树 vs 哈希表
Hash表比较适合做等值查询,不适合做范围查询。
③B+树 vs 二叉树
对于有N个叶节点的B+Tree,其搜索复杂度为O(logdN),其中d表示允许最大叶节点数为d个。
在实际情况下,d通常是大于100的,这就表示在千万级别的记录情况下,B+数的高度仍然维持在3-4层左右,即一次查询仅仅需要3-4此磁盘I/O/
而二叉树仅仅有两个子节点,树的高度会非常高,导致每次查询会进行大量的磁盘I/O。
4.联合查询的范围?
联合查询在使用时要满足最左匹配的原则。
5.什么时候需要创建索引?
- 字段有唯一性限制,比如商品的id
- 经常用于where查询的字段,这样能提升查询速度,如果条件不是一个字段可以创建联合索引。
- 经常用户Group By和Order By的字段,数据库在生成索引时,即已经以该字段排序,查询结构无需再次排序。
6.什么时候不用索引?
- 数据库特别小时没有必要用索引。
- 字段中存在大量重复的数据,不建立索引,比如性别字段,男女记录均匀分配,无论搜索哪一个字段都可能得到一半数据还不如不用索引。MySQL有一个优化器,发现某个值在表的出现频率很高时,就会忽略索引,进行全表扫描。
- 在where子句,Group By和Order By中用不上的字段。
- 经常更新的字段无需建立索引,比如不要对电商项目的用户账户余额建立索引,由于这样的索引字段被频繁修改,由于要维护B+Tree的索引有序性,就需要频繁重建索引,这个过程会很耗费数据库性能。
7.如何进行索引的优化?
- 前缀索引法
- 覆盖索引
- 主键索引最好是自增的
- 防止索引失效
①前缀索引法:如果一个字段的字符串太长,可以考虑用字符串的前几个字符建立索引,这样不仅仅可以提升查找速度还可以减少索引的大小。
前缀索引法的局限性:
- order by无法使用前缀索引(因为order by的查询结果要根据字符串的全部来排序)
- 前缀索引无法引用为覆盖索引
②覆盖索引:该索引就已经包含结果集要找的字段,避免了查找出记录的全字段的麻烦,避免了大量的回表操作和I/O操作。
③主键索引最好是自增的:
- 如果主键索引是自增的,即记录会按照顺序插入,则插入后的记录就是有序的,插入时B+树无需再变动以前的记录的位置和结构,速度更快。当页面满再开辟一个新页面即可。
- 如果主键时非自增的,则记录的主键值都是随机的,每次插入新的数据,就可能出现再数据页的中间某个位置,这将不得不移动其他记录的位置来满足新插入的记录,甚至需要将数据复制到一个新的页面,我们通常称之为页分裂,页分裂会造成大量的存储碎片会造成存储密度下降,结构不紧凑,从而影响查询效率。
④防止索引失效:
- 不用索引的最左查找和左右查找,即"%xxx"、"%xxx%"
- 在where字句中不用or
- 在使用联合索引时,符合最左匹配原则
- 不对索引进行计算、函数、类型转换等操作,这样会导致索引失效
8.如何从数据结构方面认识B+树?
①B+树叶节点的结构:
- 文件头:表示页的信息
- 页头:表示页的状态信息
- 最大、最小记录:两个虚拟的伪记录,分别表示页中最大和最小的记录
- 用户记录:存储记录内容
- 空闲空间:页中还没有用到的空间
- 页目录:存储用户记录的相对位置
- 页尾巴:检验记录是否完整
②B+树中页节点中记录是如何组织的?
页中的数据是通过单项链表串联起来的,便于插入和删除,但是检索效率不高,索引需要页目录来帮助检索。
③页目录在页节点中是什么样的?
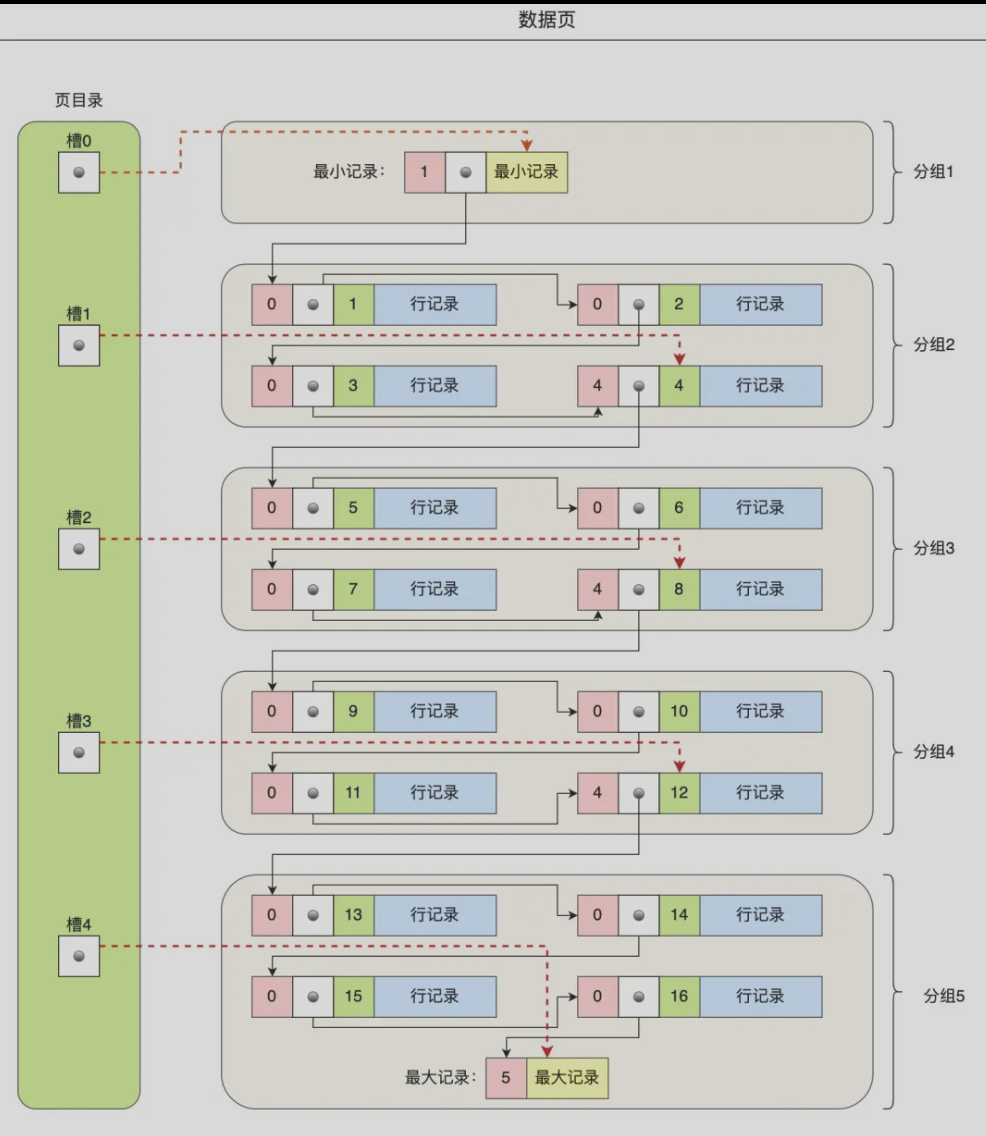
页目录建立的过程:
①首先对页中的记录进行分组,这些记录包含最大记录和最小记录,但是不含被标记删除的字段。
②该组最后一条记录来作为该组最大的记录,并且该组最大的记录中头信息会存储该组有多少记录
③页目录用来存储每组最大记录的地址偏移量,这些偏移量会被顺序存储。这些偏移量又被称之为槽,槽即使指向每组最大记录的指针。
分组的规则(有效避免分组内记录过多,查找时间复杂度衰退到O(n)):
- 第一个分组仅有一条记录
- 最后一个分组的记录数量在1-8之间
- 剩下的分组的数量在4-8之间
9.聚簇索引和二级索引的区别?
- 聚簇索引的叶节点存放的是实际数据,所有完整的用户记录都在叶子节点
- 二级索引的叶节点存放的是主键数据,如果要找到其他字段需要进行回表操作
10.B+树作为索引的优点
- 单点查询:B+树在做查询时从时间代价上来看会比B树更加稳定,且可以节约大量的I/O时间。而且由于B+树的非叶子节点不含有记录数据,则在同等情况下B+树的非叶节点可以存储更多的索引数据,在同等条件下,B+树会比B树更加矮胖。
- 插入和删除效率:B+树中有大量的冗余节点,这使得B+树在做删除时,甚至只需要将叶子节点的数据删除,无需调整非叶节点,这样删除效率非常快。插入操作:B+树的插入操作也一样,有冗余节点,但是插入可能存在节点的分裂(如果节点饱和),但是最多只涉及一条路径。而且B+树会自平衡,无需复杂的算法,类似红黑树的旋转操作等。
- 范围查询:B+树的叶子节点之间时用双向链表进行连接,这样的好处是既能像右遍历,又能向左遍历,这对范围查询非常友好。