一些特殊的组合数列

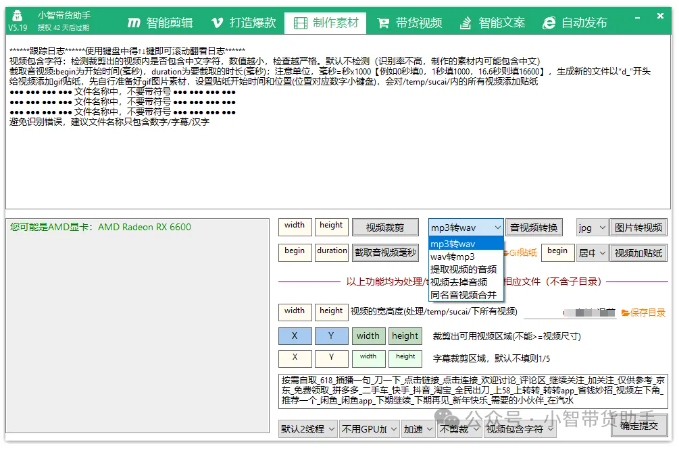
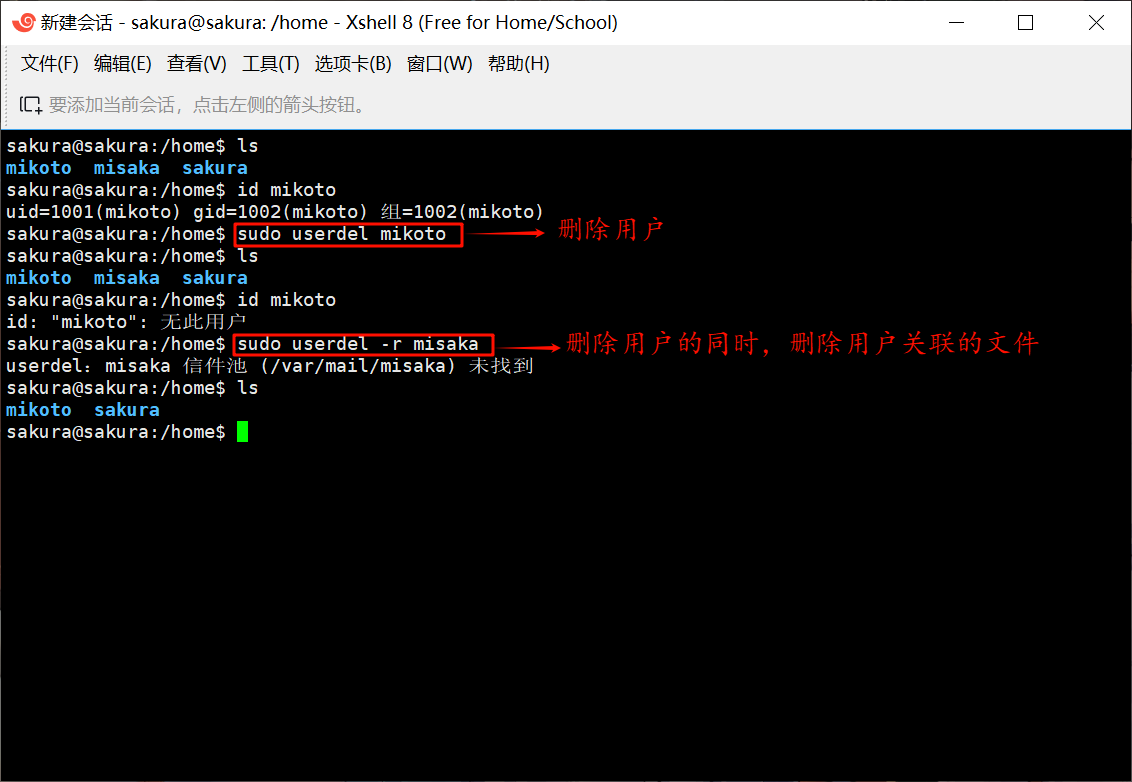
组合小杂烩

卡特兰数

Catalan 数列 \(H_n\) 有三个表达式：

\[\begin{aligned} H_n&= \begin{cases} \sum\limits_{i=0}^{n-1}H_iH_{n-i-1}&(n\ge2)\\ 1&(n=0,1) \end{cases}\\ &={H_{n-1}(4n-2)\over n+1}\\ &={2n\choose n}-{2n\choose n-1}={{2n\choose n}\over n+1} \end{aligned} \]

Catalan 数列的组合意义

• \(n\times n\) 方格图要从左下走到右上，只能经过左下到右上的对角线和对角线下方的点的方案数。
• 圆上 \(2n\) 个点成对连成 \(n\) 条弦互不相交的方案数。
• 一个栈，\(n\) 个元素依次进栈，出栈的方案数。
• 对角线不相交的情况下将 \(n\) 个节点的凸多边形延对角线划分成三角形的方案数。
• \(n\) 个节点构成不同二叉树的方案数
• \(\cdots\)

上面几种应用或都隐含了相似之处：两维之间一维一定比另一维小。如走方格时向上走步数必定 \(\le\) 向右走；栈中每一时刻出栈数必定 \(\le\) 入栈；二叉树可添加节点一定大于已有节点等等。

关于 \(O(n^2)\) 递推式，划分圆与凸多边形可以很好解释。即指定一点，枚举连到其他点分割产生两个图形的方案数乘积并累加。

下面我们给出封闭形式的证明。

Catalan 数列的证明

我们从 \(O(n^2)\) 递推式入手，设它的普通生成函数为 \(H(x)\)。

\[H(x)=\sum_{n\ge 0}H_nx^n \]

按递推式展开，拿出 \(n=0\) 项（避免下标为负），有：

\[1+\sum_{n\ge1}\sum_{i=0}^{n-1}H_ix^iH_{n-i-1}x^{n-i-1}x \]

交换求和次序，用 \(n-1\) 替换 \(n\) 有：

\[1+x\sum_{i\ge0}H_ix^i\sum_{n\ge0}H_{n-i}x^{n-i} \]

出现了两个 \(H(x)\) 的卷积，即有：

\[1+xH^2(x) \]

得到方程

\[H(x)=1+xH^2(x) \]

解得 \(H(x)\) 封闭形式

\[H(x)={1\pm\sqrt{1-4x}\over 2x} \]

封闭形式只有一个，我们将分子有理化

\[H(x)={2\over 1\mp\sqrt{1-4x}} \]

再带入 \(x=0\)，得到 \(H_0\) 为 \(1\) 的即是正确的答案；分母为 \(0\) 的不收敛，舍去。所以有唯一封闭形式

\[H(x)={2\over 1+\sqrt{1-4x}}={1-\sqrt{1-4x}\over 2x} \]

用广义二项式定理展开根式，单独处理 \(n=0\) 项，有

\[\begin{aligned} (1-4x)^{1\over2}&=\sum_{n\ge0}{{1\over2}\choose n}(-4x)^n\\&=1+\sum_{n\ge1}{({1\over2})^\underline n\over n!}(-4x)^n \end{aligned} \]

其中

\[\begin{aligned} ({1\over2})^{\underline n}&={1\over2}{-1\over2}{-3\over2}\cdots{-(2n-3)\over2}\\ &={(-1)^{n-1}(2n-3)!!\over 2^n}\\ \end{aligned} \]

同乘 \((2n-3)!!\)，有

\[{(-1)^{n-1}(2n-2)!!\over 2^n(2n-2)!}\\ \]

分母把双阶乘项的 \(2\) 都提出来，有

\[{(-1)^{n-1}(2n-2)!\over2^{2n-1}(n-1)!} \]

带回展开的二项式，得

\[(1-4x)^{1\over2}=1+\sum_{n\ge1}{(-1)^{n-1}(2n-2)!\over2^{2n-1}(n-1)!n!}(-4x)^n \]

约掉负号和 \(2^{2n-1}\)，得到

\[1-\sum_{n\ge1}{(2n-2)!\over(n-1)!n!}2x^n \]

化成组合数即

\[1-\sum_{n\ge1}{2n-1\choose n}{1\over2n-1}2x^n \]

带回原式有

\[\begin{aligned} H(x)={1-\sqrt{1-4x}\over 2x}&={1\over2x}\sum_{n\ge1}{2n-1\choose n}{1\over 2n-1}2x^n\\ &=\sum_{n\ge1}{2n-1\choose n}{1\over2n-1}x^{n-1} \end{aligned} \]

用 \(n+1\) 替换 \(n\)，有

\[\sum_{n\ge0}{2n+1\choose n}{1\over2n+1}x^{n} \]

最后吸收公式，得到

\[\sum_{n\ge0}{2n\choose n}{1\over n+1}x^n \]

即有通项公式

\[H_n={2n\choose n}{1\over n+1} \]

得证。

斯特林数