题目:
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
输入格式:
输入说明:输入数据的第1行给出4个正整数N、M、S、D,其中N(2≤N≤500)是城市的个数,顺便假设城市的编号为0~(N−1);M是高速公路的条数;S是出发地的城市编号;D是目的地的城市编号。随后的M行中,每行给出一条高速公路的信息,分别是:城市1、城市2、高速公路长度、收费额,中间用空格分开,数字均为整数且不超过500。输入保证解的存在。
输出格式:
在一行里输出路径的长度和收费总额,数字间以空格分隔,输出结尾不能有多余空格。
输入样例:
4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 20
输出样例:
3 40
代码及注释:
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>#define MAX_VERTEX_NUM 500
#define MAX_DIST 501
#define MAX_COST 501
#define ERROR -1typedef int Vertex;struct _Edge
{Vertex V, W;int dist, cost;
};
typedef struct _Edge *Edge;struct _MGraph
{int Nv, Ne;int dist[MAX_VERTEX_NUM][MAX_VERTEX_NUM];int cost[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
};
typedef struct _MGraph *MGraph; /* 以邻接矩阵存储的图的类型 */void InsertEdge(MGraph G, Edge E); // 插入边
MGraph CreateGraph(int vertexNum); // 初始化图
MGraph BuildGraph();Vertex FindMinDist(MGraph G, int dist[], bool collected[]);
void Dijkstra(MGraph G, int dist[], int cost[], Vertex S);Vertex src, dst;
// 对于全局的int数组自动初始化为0,bool数组初始化为false
int dist[MAX_VERTEX_NUM];
int cost[MAX_VERTEX_NUM];
bool collected[MAX_VERTEX_NUM];/*
07-图6 旅游规划
https://pintia.cn/problem-sets/1667128414987735040/exam/problems/1667128415088398337难度:2颗星4 5 0 3
0 1 1 20
1 3 2 30
0 3 4 10
0 2 2 20
2 3 1 203 40*/int main()
{MGraph G = BuildGraph();Dijkstra(G, dist, cost, src);printf("%d %d\n", dist[dst], cost[dst]);free(G);return 0;
}MGraph CreateGraph(int vertexNum)
{MGraph G = (MGraph)malloc(sizeof(struct _MGraph));G->Nv = vertexNum;G->Ne = 0;Vertex V, W;for (V = 0; V < vertexNum; V++){for (W = 0; W < vertexNum; W++){G->dist[V][W] = MAX_DIST;G->cost[V][W] = MAX_COST;}}return G;
}void InsertEdge(MGraph G, Edge E)
{/* 插入边<V,W> */G->dist[E->V][E->W] = E->dist;G->cost[E->V][E->W] = E->cost;/* 若是无向图则要反向也插入 */G->dist[E->W][E->V] = E->dist;G->cost[E->W][E->V] = E->cost;
}MGraph BuildGraph()
{MGraph G;Edge E;int Nv, Ne;scanf("%d %d %d %d", &Nv, &Ne, &src, &dst);G = CreateGraph(Nv);if (Ne){G->Ne = Ne;E = (Edge)malloc(sizeof(struct _Edge));for (int i = 0; i < G->Ne; i++){scanf("%d %d %d %d", &E->V, &E->W, &E->dist, &E->cost);InsertEdge(G, E);}free(E);}return G;
}Vertex FindMinDist(MGraph G, int dist[], bool collected[])
{ /* 返回未被收录顶点中dist最小者 */Vertex minV = ERROR;int minDist = MAX_DIST;for (Vertex V = 0; V < G->Nv; V++){if (collected[V] == false && minDist > dist[V]){/* 若V未被收录,且dist[V]更小 */minDist = dist[V]; /* 更新最小距离 */minV = V; /* 更新对应顶点 */}}if (minDist < MAX_DIST) /* 若找到最小dist */return minV; /* 返回对应的顶点下标 */elsereturn ERROR; /* 若这样的顶点不存在,返回错误标记 */
}void Dijkstra(MGraph G, int dist[], int cost[], Vertex S)
{Vertex V, W;/* 初始化:此处默认邻接矩阵中不存在的边用INFINITY表示 */for (V = 0; V < G->Nv; V++){dist[V] = G->dist[S][V];cost[V] = G->cost[S][V];}/* 先将起点收入集合 */dist[S] = 0;cost[S] = 0;collected[S] = true;while (1){/* V = 未被收录顶点中dist最小者 */V = FindMinDist(G, dist, collected);if (V == ERROR) /* 若这样的V不存在 */break; /* 算法结束 */collected[V] = true; /* 收录V */for (W = 0; W < G->Nv; W++) /* 对图中的每个顶点W *//* 若W是V的邻接点并且未被收录 */if (collected[W] == false && G->dist[V][W] < MAX_DIST){if (G->dist[V][W] < 0) /* 若有负边 */return; /* 不能正确解决,返回错误标记 *//* 若收录V使得dist[W]变小 */if (dist[V] + G->dist[V][W] < dist[W]){dist[W] = dist[V] + G->dist[V][W]; /* 更新dist[W] */cost[W] = cost[V] + G->cost[V][W];}else if (dist[V] + G->dist[V][W] == dist[W] &&cost[V] + G->cost[V][W] < cost[W]){cost[W] = cost[V] + G->cost[V][W];}}} /* while结束*/
}
ChatGPT对代码的分析,评估:
定义了合适的常量:MAX_DIST 和 MAX_COST 的定义符合题目要求,对于表示距离和花费的最大值都设置为 501,有效地区分了有限距离和无穷远的情况。
创建图和插入边:CreateGraph 和 InsertEdge 函数用于创建图和插入边的操作,实现了初始化图的邻接矩阵并向图中添加边的功能。
构建图:BuildGraph 函数根据输入构建了图,并通过调用 CreateGraph 和 InsertEdge 来创建和填充图的邻接矩阵。
Dijkstra 算法:Dijkstra 函数使用 Dijkstra 算法,根据图的邻接矩阵计算从起点到每个顶点的最短距离和最小花费。在这个过程中,使用了辅助函数 FindMinDist 来选择未被收录顶点中距离最小的顶点。
主函数运行:主函数中先调用 BuildGraph 构建图,然后调用 Dijkstra 计算最短距离和最小花费,并输出结果。
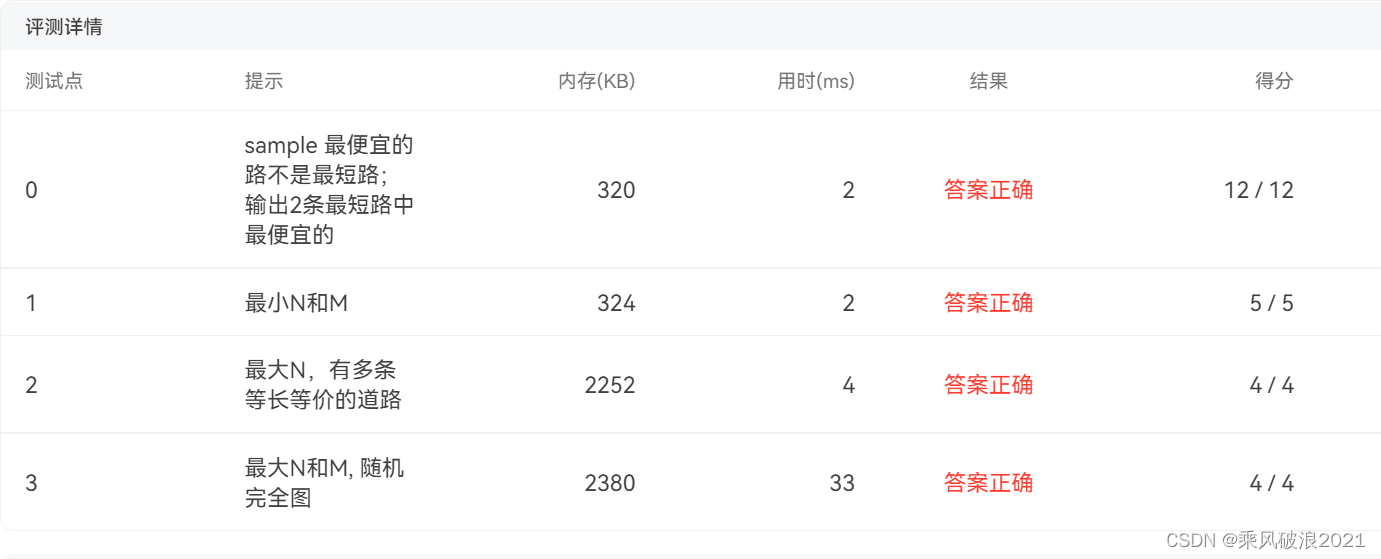
执行结果: