题目大意
原题链接
给你一个大小为 \(n \times n\) 的矩阵,上面有 \(n\) 条线段(一行一条)。你只能向右,向下,向左走。每一条线段都必须完整的经过。请问从 \((1,1)\) 到 \((n,n)\) 最短路径长度是多少?
解法
这道题可以使用最短路或者DP来做。我觉得DP本题更简单一点所以我这里用的是DP。
可以设 \(dp_{i,0/1}\) 表示目前我已经看到第 \(i\) 行现在处于这条线段上的左边左端点还是右端点。(\(0\) 为左端点,\(1\) 为右端点)
于是我们就可以想到最初步的方法:每一次枚举从上一行的线段的左端点来还是右端点来,然后直接从选那个端点到当前的线段的左右个端点。即(以 \(dp_{i,0}\) 为例子):
\(dp_{i,0}=\min(dp_{i-1,0}+|l_{i-1}-l_{i}|,dp_{i-1,1}+|r_{i-1}-l_i|)+1\)
然后样例都没过,呜呜。
就不放代码了
我们想想我们少了些什么?我们不能保证每一个线段到我们都完整的走过去。那我们应该怎么走呢?如下图:
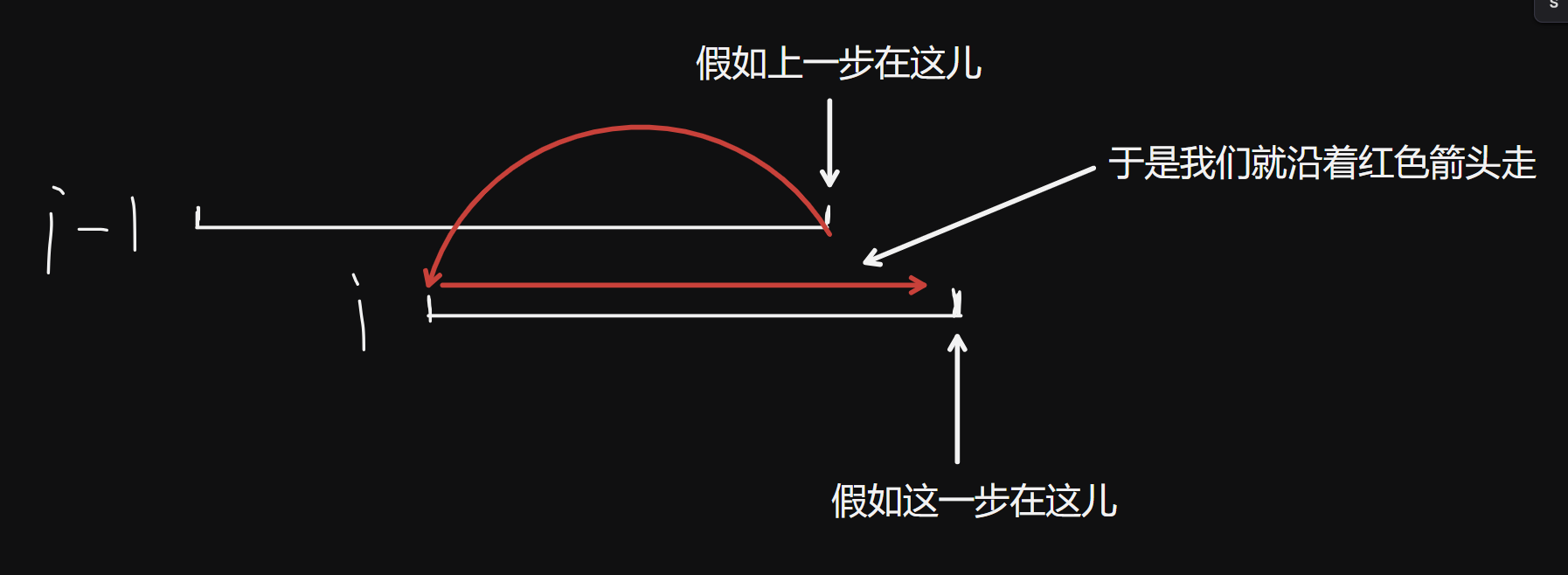
沿着这个我们又可以得出新的DP方程(以 \(dp_{i,0}\) 为例):
\(dp_{i,0}=\min(dp_{i-1,0}+|l_{i-1}-r_i|+r_i-l_i+1,dp_{i-1,1}+abs(r_{i-1}-r_i)+r_i-l_i+1)\)
得到代码:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e4+5;
int l[maxn],r[maxn],dp[maxn][2];
signed main()
{ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);int n;cin>>n;for(int i=1;i<=n;i++) cin>>l[i]>>r[i];dp[1][0]=r[1]+r[1]-l[1]-1,dp[1][1]=r[1]-1;//初始化for(int i=2;i<=n;i++){dp[i][0]=min(dp[i-1][0]+abs(l[i-1]-r[i])+r[i]-l[i],dp[i-1][1]+abs(r[i-1]-r[i])+r[i]-l[i])+1;dp[i][1]=min(dp[i-1][1]+abs(l[i-1]-l[i])+r[i]-l[i],dp[i-1][1]+abs(r[i-1]-l[i])+r[i]-l[i])+1;}cout<<min(dp[n][0],dp[n][1])+r[n]-l[n];//最后一次我们还没考虑return 0;
}
上洛古一交,得到:

14分
还少了点什么?原来我们的初始化和最后一次也不对。具体的可以见下图:
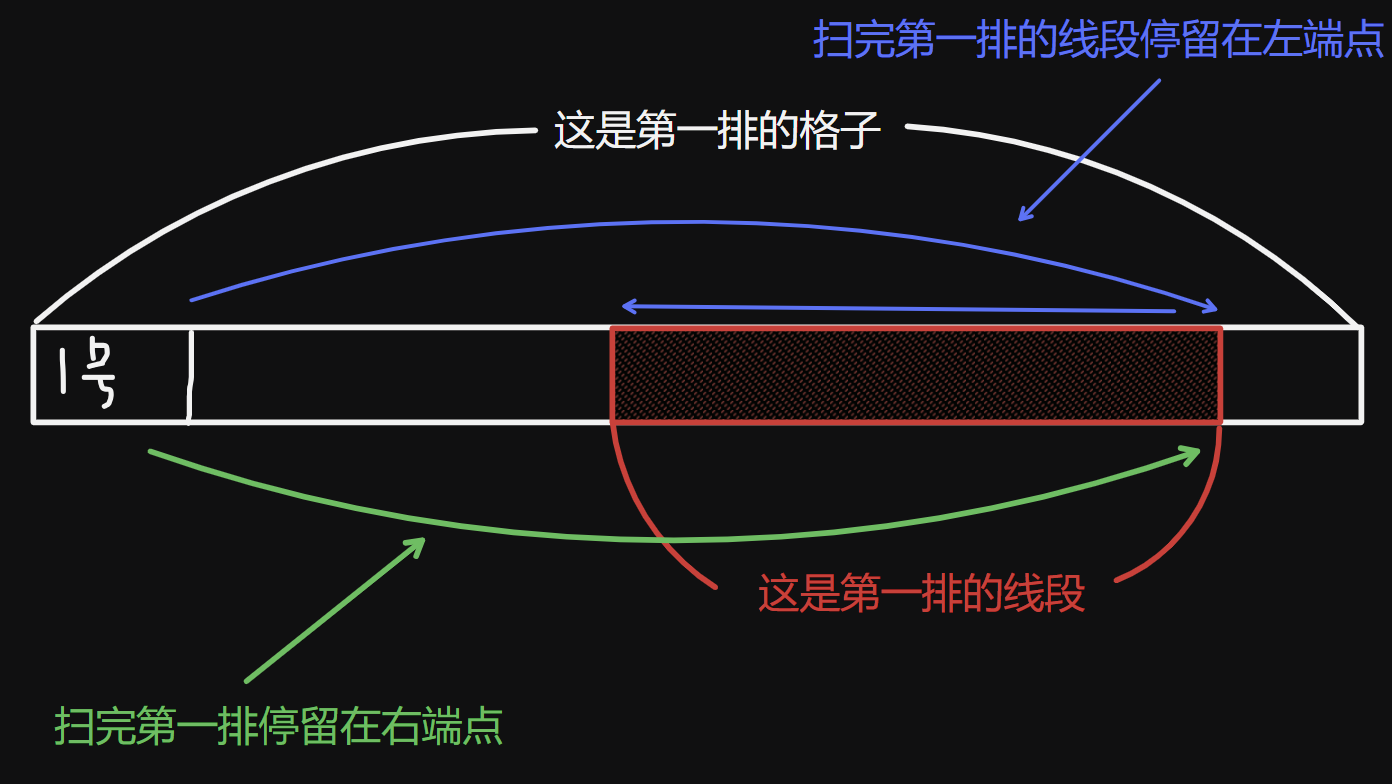
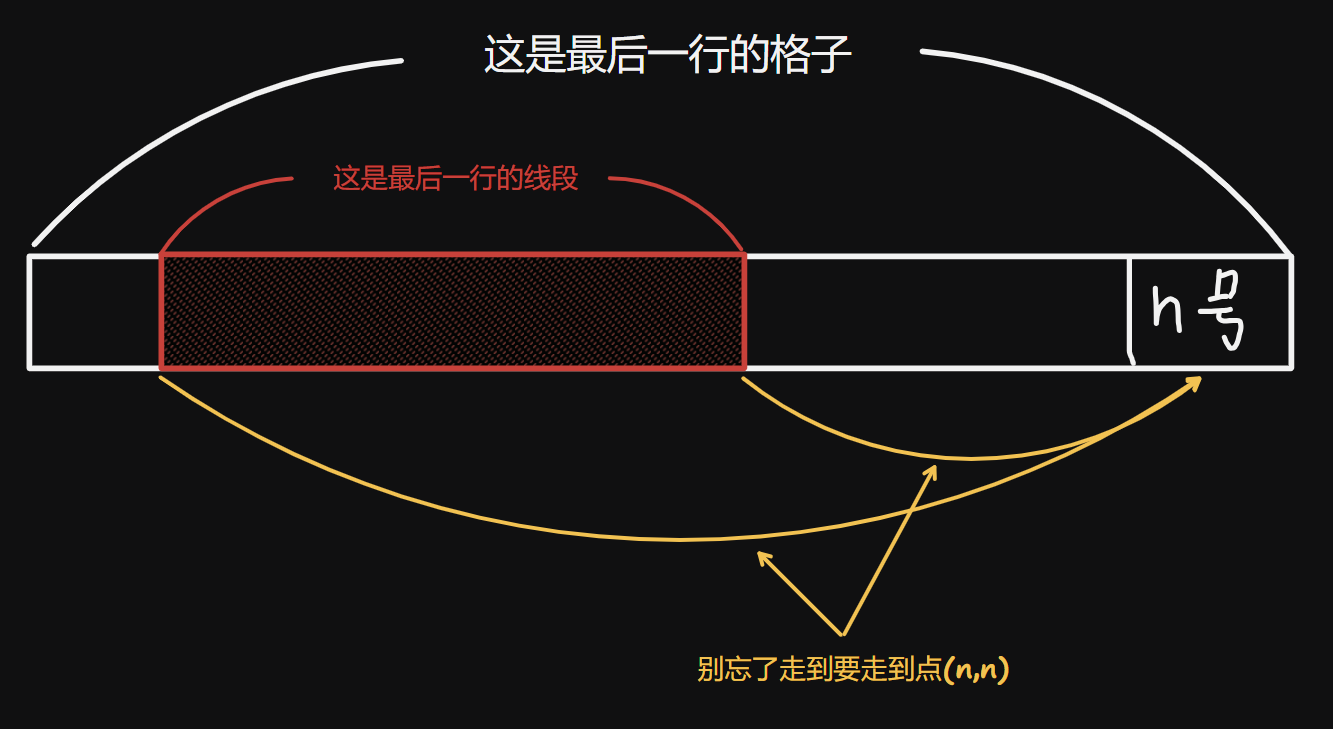
最后一次(答案):
于是修改一下初始化:
\(dp_{1,0}=r_1+r_1-l_1-1,dp_{1,1}=r_1-1\)
最后一行(答案):
\(\min(dp_{n,0}+n-l_n,dp_{n,1}+n-r_n)\)
真正的AC代码:终于完了
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=2e4+5;
int l[maxn],r[maxn],dp[maxn][2];
signed main()
{ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);int n;cin>>n;for(int i=1;i<=n;i++) cin>>l[i]>>r[i];dp[1][0]=r[1]+r[1]-l[1]-1,dp[1][1]=r[1]-1;for(int i=2;i<=n;i++){dp[i][0]=min(dp[i-1][0]+abs(l[i-1]-r[i])+r[i]-l[i]+1,dp[i-1][1]+abs(r[i-1]-r[i])+r[i]-l[i]+1);dp[i][1]=min(dp[i-1][0]+abs(l[i-1]-l[i])+r[i]-l[i]+1,dp[i-1][1]+abs(r[i-1]-l[i])+r[i]-l[i]+1);}cout<<min(dp[n][0]+n-l[n],dp[n][1]+n-r[n]);return 0;
}