P8626 [蓝桥杯 2015 省 A] 灾后重建 解题报告

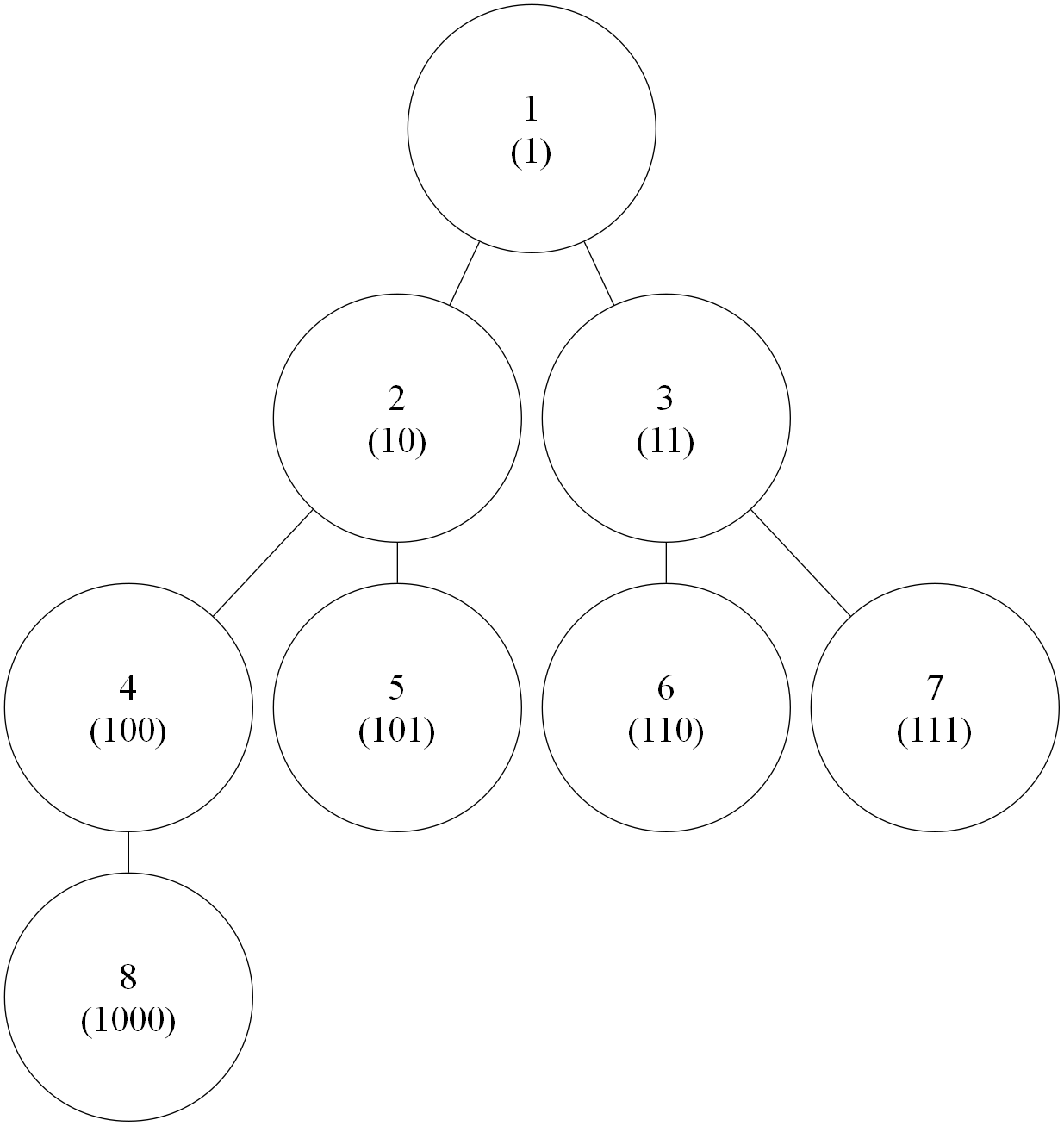
一个结论，如果要让路径上的最大值最小，路径必然在原图的最小生成树上。

因为如果不在，那么经过的非树边的权值必然会小于会与它组成环的树边的最大值，此时就可以替换。

看到题目中的 \(k\)，可以根号分治。

当 \(k>\sqrt n\) 的时候，需要计算的点的数量就 \(<\sqrt n\)，不超过 250 个，就可以暴力枚举每个点。

因为是 \(max\)，可以重复计算，根据 LCA 的性质，每一次只需要在上一个点求解完后的最近公共祖先的基础上叠加计算。

时间复杂度 \(O(q\sqrt n logn)\)

对于剩下的部分，因为 \(k\) 很小，情况很少，所以可以预处理出每一个 \(i\) 到 \(i+k\) 的贡献。

此时，对于每个余数，建线段树，然后 \(O(logn)\) 求解即可。

但是这样的空间复杂度很大，考虑优化。

注意到题目中没有限制强制在线，可以离线处理，将所有询问按 \(k\) 为第一关键字，\(c\) 为第二关键字排序。

此时，可以在 \(k\) 改变时更新 \(n\) 个数的贡献，\(c\) 或 \(k\) 改变时，重新建线段树。

此时，更新和查询的时间复杂度均为 \(O(n\sqrt n logn)\)。

代码：

#include<cstdio>
#include<algorithm>
#include<cmath>
#define lid id<<1
#define rid id<<1|1
using namespace std;
int n,m,q,head[50005],edgenum;
struct node{int u,v,w;
}a[200005];
struct edge{int to,nxt,val;
}e[100005];
struct ques{int l,r,k,c,id;
}qs[50005];
void add_edge(int u,int v,int w)
{e[++edgenum].nxt=head[u];e[edgenum].to=v;e[edgenum].val=w;head[u]=edgenum;
}
bool cmp(node x,node y)
{return x.w<y.w;
}
int f[50005];
int find(int x)
{if(f[x]!=x) f[x]=find(f[x]);return f[x];
}
int f1[50005][18],dep[50005],d[50005][18];
int dfn[50005],tot,ans[50005];
void dfs(int u,int fa)
{dep[u]=dep[fa]+1,f1[u][0]=fa;dfn[u]=++tot;for(int i=1;i<=16;i++){f1[u][i]=f1[f1[u][i-1]][i-1];d[u][i]=max(d[u][i-1],d[f1[u][i-1]][i-1]);}for(int i=head[u];i;i=e[i].nxt){int v=e[i].to;if(v==fa) continue;d[v][0]=e[i].val;dfs(v,u);}
}
bool cmp1(ques x,ques y)
{if(x.k==y.k) return x.c<y.c;return x.k<y.k;
}
int lca,mx;
void getlca(int x,int y)
{if(dep[x]<dep[y]) swap(x,y);mx=0;for(int i=16;i>=0;i--){if(dep[f1[x][i]]>=dep[y]){mx=max(mx,d[x][i]);x=f1[x][i];}if(x==y){lca=x;return;}}for(int i=16;i>=0;i--){if(f1[x][i]!=f1[y][i]){mx=max(mx,max(d[x][i],d[y][i]));x=f1[x][i],y=f1[y][i];}}lca=f1[x][0],mx=max(mx,max(d[x][0],d[y][0]));
}
int get(int l,int r,int k,int c)
{int st=l/k;st=st*k+c;if(st<l) st+=k;int lc=st,res=0;for(int i=st+k;i<=r;i+=k){getlca(lc,i);res=max(res,mx);lc=lca;}return res;
}
int p[50005],b[50005],cnt;
void getarr(int x)
{for(int i=1;i<=n;i++) p[i]=0;for(int i=1;i<=n-x;i++){getlca(i,i+x);p[i]=mx;}
}
struct seg_tr{int l,r,val;
}tr[200005];
void build(int id,int l,int r)
{tr[id].l=l,tr[id].r=r;if(l==r){tr[id].val=b[l];return;}int mid=(l+r)>>1;build(lid,l,mid);build(rid,mid+1,r);tr[id].val=max(tr[lid].val,tr[rid].val);
}
int query(int id,int l,int r)
{if(tr[id].l==l&&tr[id].r==r){return tr[id].val;}int mid=(tr[id].l+tr[id].r)>>1;if(r<=mid) return query(lid,l,r);else if(l>mid) return query(rid,l,r);else return max(query(lid,l,mid),query(rid,mid+1,r));
}
void new_tr(int x,int y)
{if(y==0) y=x;cnt=0;for(int i=y;i<=n-x;i+=x){b[++cnt]=p[i];}build(1,1,cnt);
}
int getans(int l,int r,int k,int c)
{int st=l/k,ed=r/k;if(c==0){st=(l+k-1)/k;return query(1,st,ed-1);}if(st*k+c<l) st++;if(ed*k+c>r) ed--;
//	printf("%d %d %d\n",st,ed,cnt);return query(1,st+1,ed);
}
int main()
{scanf("%d%d%d",&n,&m,&q);for(int i=1;i<=m;i++){int u,v,w;scanf("%d%d%d",&u,&v,&w);a[i]=(node){u,v,w};}for(int i=1;i<=q;i++){int l,r,k,c;scanf("%d%d%d%d",&l,&r,&k,&c);qs[i]=(ques){l,r,k,c,i};}sort(a+1,a+m+1,cmp);for(int i=1;i<=n;i++) f[i]=i;for(int i=1;i<=m;i++){int u=a[i].u,v=a[i].v;if(find(u)==find(v)) continue;f[find(u)]=find(v);add_edge(u,v,a[i].w);add_edge(v,u,a[i].w);}dfs(1,0);sort(qs+1,qs+q+1,cmp1);int len=sqrt(n);
//	printf("1");for(int i=1;i<=q;i++){if(qs[i].k>len){
//		printf("%d",i);ans[qs[i].id]=get(qs[i].l,qs[i].r,qs[i].k,qs[i].c);continue;}if(qs[i].k!=qs[i-1].k){getarr(qs[i].k);
//			for(int j=1;j<=n;j++)
//			{
//				printf("%d ",p[j]);
//			}
//			printf("\n");new_tr(qs[i].k,qs[i].c);}else if(qs[i].c!=qs[i-1].c){new_tr(qs[i].k,qs[i].c);}
//		printf("%d ",qs[i].id);ans[qs[i].id]=getans(qs[i].l,qs[i].r,qs[i].k,qs[i].c);}
//	printf("1");for(int i=1;i<=q;i++){printf("%d\n",ans[i]);}return 0;
}