状压dp串讲

news/2025/2/5 21:27:43/文章来源:https://www.cnblogs.com/EagleChenzhilong/p/18700174

知识讲解

前置知识：位运算

（学过的可以跳过）

众所周知，电脑使用的是二进制，那么对二进制位进行的计算就叫做位运算。那么经典的位运算有以下几种：

&（按位与）规律：除非两者均为 \(1\)，否则其他情况结果均为 \(0\)。若两者为均唯一则答案为 \(1\)。
|（按位或）规律：除非两者均为 \(1\)，否则其他情况答案为 \(1\)。若两者答案均为零则答案为 \(0\)。
~（按位取反）规律：一位一位看，如果说当前这一位 \(0\) 则更新为 \(1\)，若当前这一位为 \(1\) 则更新为 \(0\)。
^或者\(\bigoplus\)（按位异或）规律：相同为零，不同为一。
<<（按位左移）规律：将二进制位向左移动若干位。
>>（按位右移）规律：将二进制位向右移动若干位。

如：
\(1\&1=1,1\&0=0,0\&1=0,0\&0=0\)
\(1|1=1,1|0=1,0|1=1,0|0=0\)
按位取反就不给例子了
\(1\bigoplus1=0,1\bigoplus0=1,0\bigoplus1=1,0\bigoplus0=0\)
按位移也不给了。

状压dp

我们经常会遇到一些情况：他的状态特别多，但是每一个状态很少（通常只有两个）。这个时候我们就可以考虑把这些状态全部压到一个数里面。这个数的每一位就表示了我们当前的状态。当我们对这个状态进行DP的时候就被称为状压DP。

一些例题

1.Traveling Salesman among Aerial Cities

原题链接（洛谷）

原题链接（atcoder）

给你 \(n\) 个点（在三维坐标内），坐标位置为 \((x_i,y_i,z_i)\)。从 \((a,b,c)\) 到 \((p,q,r)\) 的代价是 \(|p-a|+|q-b|+\max(0,r-c)\)，请问从一出发一路走过所有点再回到一的最小代价是多少？

解法

这是一道状压DP的经典题型：旅行商问题。即从某个点出发一路旅行所有点之后再回到这个点的最小代价。

可以设立状态： \(dp_{i,j}\)，表示已经经过了那些点，现在在 \(j\) 号点。因为每一个点最多来一次，所以这里我们就可以使用状态压缩，将所有点是否来过压进状态 \(i\) 里面。

可以得到转移方程：\(dp_{i,j}=\min(dp_{i,j},dp_{i\bigoplus(1<<(j-1)),k}+f(k,j));\)，其中 \(f\) 函数算的是移动的代价。

初始化即为：\(dp_{0,0}=1\)。

代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=23;
int x[maxn],y[maxn],z[maxn],dp[(1<<19)][maxn];
int f(int i,int j)
{return abs(x[j]-x[i])+abs(y[j]-y[i])+max(0ll,z[j]-z[i]);
}
signed main()
{ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);int n;cin>>n;memset(dp,0x3f,sizeof(dp));for(int i=1;i<=n;i++) cin>>x[i]>>y[i]>>z[i];dp[0][0]=1;for(int i=1;i<=n;i++) dp[(1<<(i-1))][i]=0;for(int i=1;i<(1<<n);i++)for(int j=2;j<=n;j++){if(((i>>(j-1))&1)==0) continue;//如果j曾经没有被访问过，那么肯定是不行的。for(int k=1;k<=n;k++){if(((i>>(k-1))&1==0)||i==j) continue;// k是指j的上一步。如果说他没被访问过，那也肯定是不行的。dp[i][j]=min(dp[i][j],dp[i^(1<<(j-1))][k]+f(k,j));}}int ans=1e18+5;for(int i=2;i<=n;i++) ans=min(ans,dp[(1<<n)-1][i]+f(i,1));cout<<ans;return 0;
}

P1896 [SCOI2005] 互不侵犯

原题链接

求在一个 \(n\times n\) 的棋盘上面放 \(k\) 个国王其中国王不能互相攻击的方案数。国王的攻击距离如下图所示。

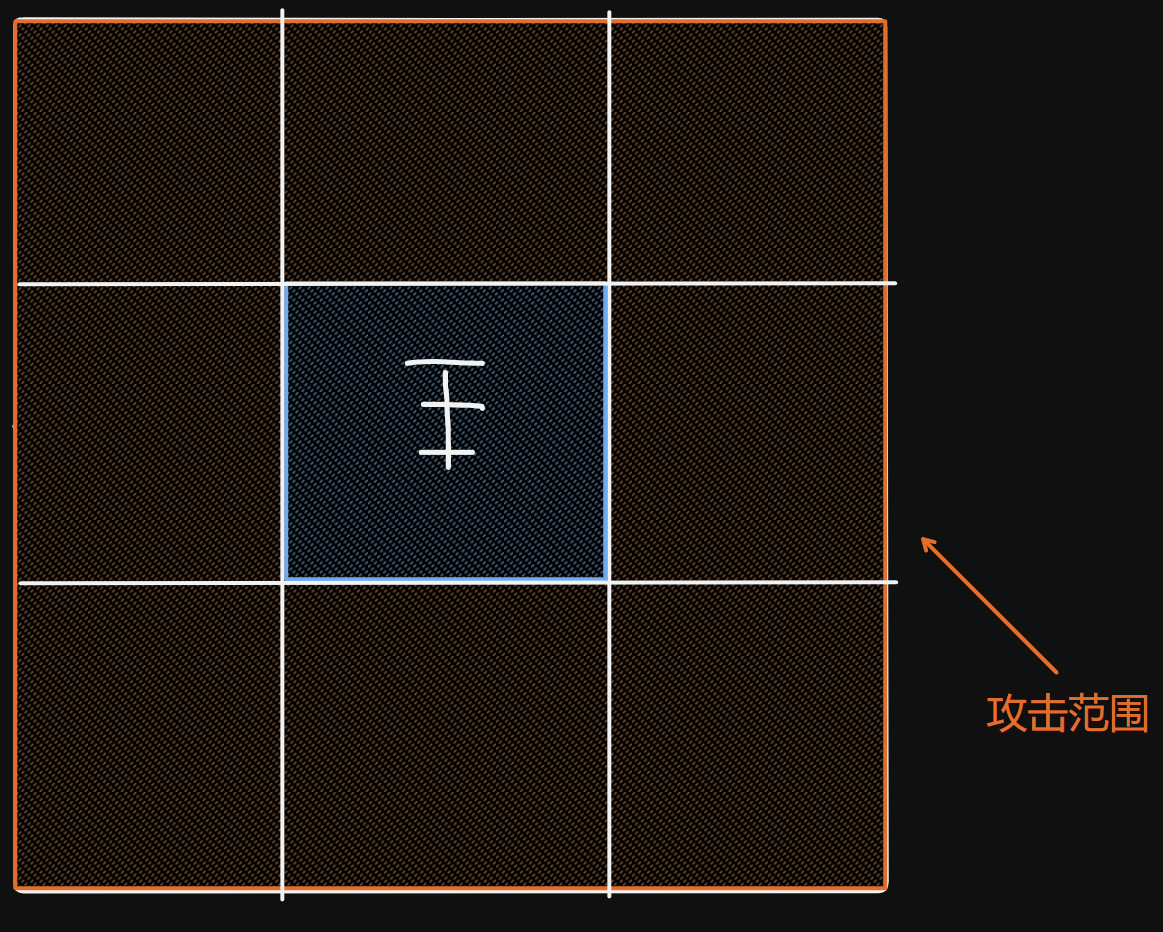
解法

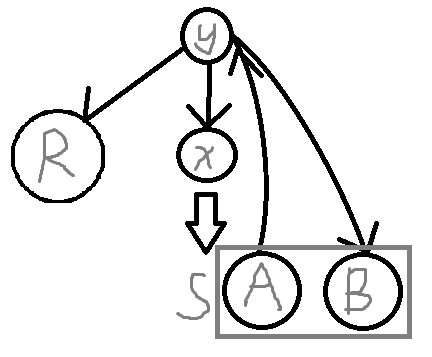
我们可以用N个状态来表示每一行他用哪些来放国王，\(1\) 表示放，\(0\) 表示不放。那如何判断其左右是否有跟它相邻的呢？见下图（左的）。

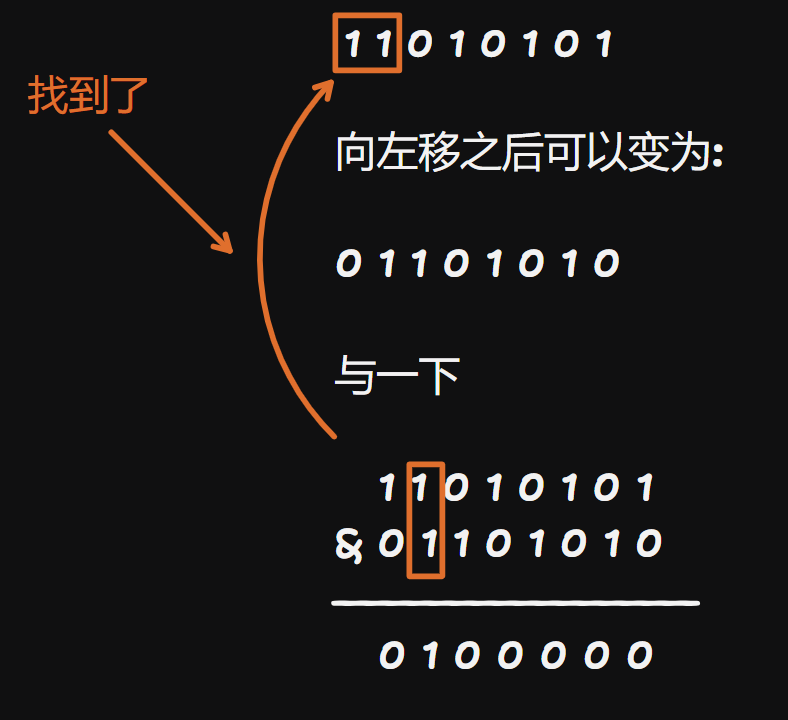
右边的，则是同理。左上与右上的也是同理。上面的是 \(这一行的 \& 上一行的\)。

然后对其进行DP。大体类似于上一道题的旅行商。但是这道题对他放的个数也有限制。所以我们还得再加一位来存当前已经放了多少个。

细节看代码：

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int maxn=15;
int dp[maxn][maxn][(1<<maxn)];//中间那一为就是用来存它当前已经放了多少个的。
int f(int x)//用来计算它当前这一行放了多少个。
{int ans=0;while(x) ans++,x-=(x&-x);return ans;
}
signed main()
{ios::sync_with_stdio(0);cin.tie(0); cout.tie(0);int n,r;cin>>n>>r;vector<int> num;for(int i=0;i<(1<<n);i++) if((i&(i>>1))==0&&(i&(i<<1))==0) num.push_back(i);//有哪些方法？在当前这一行来看是合法的。dp[0][0][0]=1;//初始化for(int i=1;i<=n;i++)//枚举行for(int j:num)//枚举这一行的状态for(int k:num)//枚举上一行的状态{if((j&k)||((j>>1)&k)||((k>>1)&j)) continue;//如果说这的正上方记的左上方记的右上方都有可能会重的话，那么肯定就是不行的，细节在上面的图中。for(int l=f(j);l<=r;l++) dp[i][l][j]+=dp[i-1][l-f(j)][k];//枚举，从第一行到现在一共放了多少个+转移}int ans=0;for(auto x:num) ans+=dp[n][r][x];//最后一道的情况我不知道，需要枚举。累积一下，求和即可。cout<<ans;return 0;
}