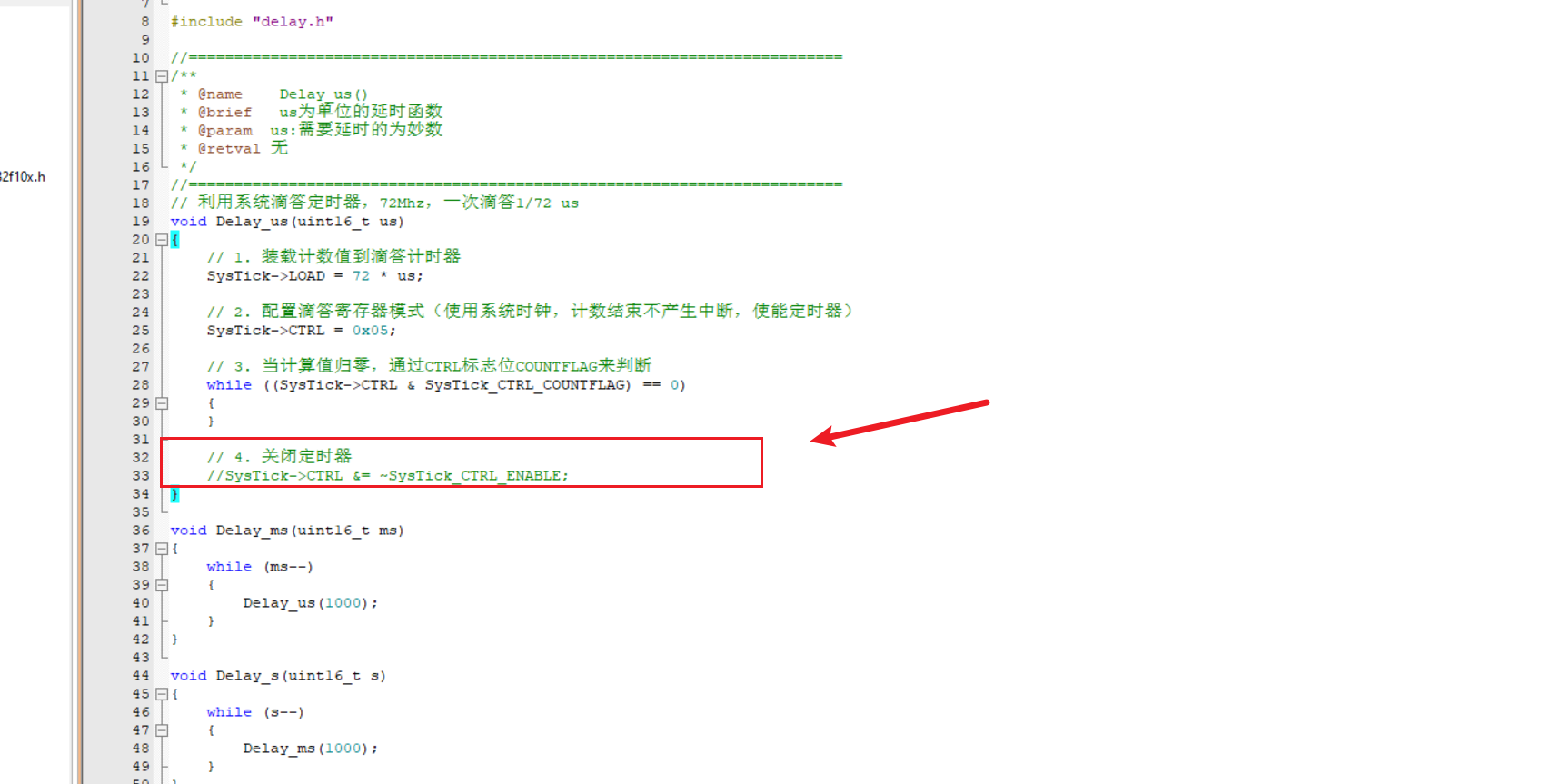
多项式乘法可以用\(O(n^{2})\)逐项得到,但不高效。而FFT可以用\(O(nlogn)\)快速计算
利用FFT来解决算法题的例子:
ABC392 G
要找给定数组中满足\(A + C = 2B\)的升序三元组\((A,B,C)\)的数量,可以通过构造多项式的方式巧妙计算:
设\(a=[1,2,3,5]\),要计算这个数组中的三元组数量:
转化为计算数组中每个元素作为\(B\)时的数量,再累加到一起。
例如计算\(B=5\)时的三元组数量,即计算\(A+C=10\)的\((A,C)\)个数。这相当于计算:
\[num(1)*num(9)+num(2)*num(8)+num(3)*num(7)+num(4)*num(6)
\]
其中\(num(i)\)表示数字\(i\)在\(a\)中出现个数。
这个操作就是卷积的计算,而计算卷积的高效算法就是FFT。对于本题,可以构造这样的多项式:
\[(x^{1} + x^{2} + x^{3} + x^{5})
\]
数组中每一项对应指数,而数组中出现了的数系数置为1,没出现的数系数置为0。计算这个多项式的平方,即:
\[(x^{1} + x^{2} + x^{3} + x^{5})(x^{1} + x^{2} + x^{3} + x^{5})
\]
上面多项式的展开结果中的每一项\(b_{i}x^{i}\)即表示\(2B=i\)的\((A,C)\)个数是\(b_{i}\)。具体见代码(用python中的numpy库实现了FFT)
code