前言
新的类型, 跟考试放的差不多的策略就行了
后面就是找时间复习, 然后找一下状态就好了
\(\rm{F}\)
看到这是个 \(\rm{C}\) 题, 先做这个
思路
给定 \(p_{i, c}\) 表示位置 \(i\) 是字符 \(c\) 的概率, 确定 \(\displaystyle\sum_{c = 1}^{t} p_{i, c} = 1\)
一个有效的信息被定义为任意长度为 \(k\) 的子序列都在集合 \(\mathbb{D}\) 中出现
求一个有效的信息 \(m_1m_2m_3m_4\cdots m_n\) , 使得 \(\displaystyle \prod_{i = 1}^{n} p_{i, m_i}\) 最大
想了一会只想出了暴力
想了一会搞了一个类似于模拟的做法
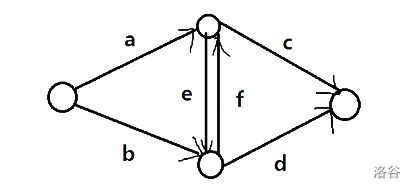
首先我们把 \(\mathbb{D}\) 中的串串丢进字典树上, 对于每一个串串, 我们不难处理出其后缀串串的下一个位置, \(\rm{belike}\):

这样我们能递归的构造信息, 每次选取的时候按照概率从大往小选即可
唯一的问题变成了一些分支最终是无解的
如果深搜就会超时, 发现贪心也是错误的
不太会, 想的方法太复杂先丢了
\(\rm{D}\)
瞎开
思路
求最长子序列使得子序列的前半部分和后半部分相同, 并输出, 接受 \(\mathcal{O} (n^2)\) 上下的复杂度
初步的想法是 \(\mathcal{O} (n)\) 划分两个子序列, 然后 \(\mathcal{O} (n)\) 找最长公共子序列
但是 \(\mathcal{O} (n)\) 找最长公共子序列怎么做, 根本没法做
为了优化时间复杂度, 可以将最长公共子序列问题转化为最长上升子序列问题
具体思路是: 统计数组 \(a\) 中的每个元素在数组 \(b\) 中出现的位置, 并按从大到小排序; 然后对这些位置求最长上升子序列, 时间复杂度为 \(\mathcal{O}(n\log n)\)
所以退而求其次, 写 \(\mathcal{O} (n^2 \log n)\) 也没什么不好的
但是发现也实现不了, 不难发现这种移动分界线问题, 肯定是靠你 \(\rm{dp}\) 去除重复操作来做的
所以思路很明晰, 问题转化为, 如何在分界线移动时均摊的求出当前的最长公共子序列
开始的时候把序列翻转记为 \(b\) , 空序列记为 \(a\)
不难发现, 每次操作相当于把 \(b\) 末尾的字母剪切到 \(a\) 里, 更新 \(\rm{dp}\) 数组
假设 \(a\) 当前的长度为 \(i\) , \(b\) 当前的长度为 \(j\) , 存在 \(dp_{i, j}\)
移动后 \(a\) 当前的长度为 \(i + 1\) , \(b\) 当前的长度为 \(j - 1\) , \(dp_{i, j}\) 废除无效, 但是 \(dp\) 数组中其他部分仍然成立
因此只需要更新 \(dp_{i + 1, j - 1}\) , 一般的
最终 \(j = 1, i = n - 1\) 时就可以结束了
然后你发现删的是前缀不能这么做
不会, 丢了
\(\rm{B}\)
过的人多, 开
思路
找一下规律发现叠加 \(k\) 有周期性
例如
但是写不了
考虑二进制下类似数位 \(\rm{dp}\) 的做法, 这样稍微复杂度正确一点
相当于记录当前的位数, 之前的 \(1\) 的个数, 对应十进制的值对 \(k\) 取模的值
如何 记忆化 / 剪枝 , 如果我们从高位到低位放, 当前高位对应是背倍数, \(\cdots\)
考虑设计状态 \(f_{p, i, m}\) 表示当前的位数, \(1\) 的个数, 当前的余数 出现了多少次
考虑转移, 从低位到高位考虑
实现中应当使用刷表法更简便
数据检验, 懒得检验, 应当是对的