【洛谷P3884】二叉树问题[JLOI2009]

这个主要是二叉树的大杂烩

[JLOI2009] 二叉树问题

题目描述

如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

• 深度：\(4\)
• 宽度：\(4\)
• 结点 8 和 6 之间的距离：\(8\)
• 结点 7 和 6 之间的距离：\(3\)

其中宽度表示二叉树上同一层最多的结点个数，节点 \(u, v\) 之间的距离表示从 \(u\) 到 \(v\) 的最短有向路径上向根节点的边数的两倍加上向叶节点的边数。

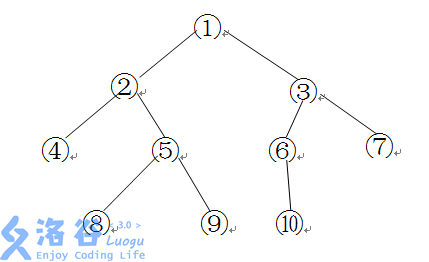
给定一颗以 1 号结点为根的二叉树，请求出其深度、宽度和两个指定节点 \(x, y\) 之间的距离。

输入格式

第一行是一个整数，表示树的结点个数 \(n\)。
接下来 \(n - 1\) 行，每行两个整数 \(u, v\)，表示树上存在一条连接 \(u, v\) 的边。
最后一行有两个整数 \(x, y\)，表示求 \(x, y\) 之间的距离。

输出格式

输出三行，每行一个整数，依次表示二叉树的深度、宽度和 \(x, y\) 之间的距离。

样例 #1

样例输入 #1

10                                
1 2                            
1 3                            
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6

样例输出 #1

4
4
8

提示

对于全部的测试点，保证 \(1 \leq u, v, x, y \leq n \leq 100\)，且给出的是一棵树。保证 \(u\) 是 \(v\) 的父结点。

解法&&个人感想

这个题目就是求深度、宽度和距离
深度顾名思义就是用DFS 而宽度在没有用广度优先遍历的情况下（本题数据较小）就可以比较同一深度的节点数
距离固然可以用LCA（最近公共祖先）但是一看数据范围这样 而且是稀疏图 可以用Floyd求最短路(O(\(N^3\)))
我们来介绍一下Floyd 其实就是一个类似DP的操作
也就是松弛操作 d[i][j]=min(d[i][j],d[i][k]+d[k][j])
有点像三角形两边之和大于第三边 但是图论里没这回事
这个有时候在全源最短路径里有奇效
P.S:注意本题对“距离”的定义 以及Floyd要用邻接矩阵存储

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int INF=1e9;
int d[105][105];
int head[1005],nex[10005],ver[10005];
int siz[105];
int vis[105];
int n,x,y,tot,sx,sy;
int bro[105];
int ans,sum;
void add(int x,int y){ver[++tot]=y;nex[tot]=head[x];head[x]=tot;
}
void dfs(int x){if(vis[x]) return ;vis[x]=1;for(int i=head[x];i;i=nex[i]){int y=ver[i];if(vis[y]==0){siz[y]=siz[x]+1;dfs(y);}}
}
int main(){ scanf("%d",&n);memset(d,0x3f,sizeof(d));for(int i=1;i<=n;i++) d[i][i]=0;for(int i=1;i<=n-1;i++){scanf("%d%d",&x,&y);add(x,y);d[x][y]=1;d[y][x]=2;}scanf("%d%d",&sx,&sy);siz[1]=1;dfs(1);for(int i=1;i<=n;i++){sum=max(sum,siz[i]);}printf("%d\n",sum);for(int i=1;i<=n;i++){bro[siz[i]]++;}for(int i=1;i<=n-1;i++){ans=max(bro[i],ans);}printf("%d\n",ans);for(int k=1;k<=n;k++){for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){d[i][j]=min(d[i][j],d[i][k]+d[k][j]);}}}printf("%d",d[sx][sy]);system("pause");return 0;
}