考虑观察最优解的一些性质:
性质 1:一个非叶子节点的入度和出度非 0。
证明:显然把任意一条邻边翻转之后会更优。
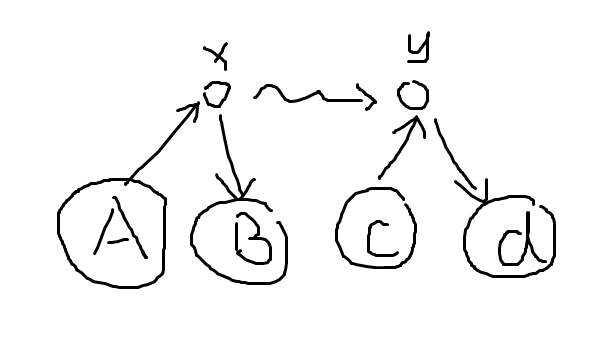
性质 2:若 \(x\) 可达 \(y\),则 \(out_x>1\) 和 \(in_y>1\) 不会同时成立。
证明:
如图,设能到 \(x\) 的点数为 \(A\),\(x\) 能到达的点数为 \(B\)(不走 \(x\rightsquigarrow y\) 路径上 \(x\) 的出边);能到 \(y\) 的点数为 \(C\)(不走 \(x\rightsquigarrow y\) 路径上 \(y\) 的入边),\(y\) 能到的点数为 \(D\)。
假设翻转所有 \(x\) 的出边及他们子树内的边(不含 \(x\rightsquigarrow y\) 路径上 \(x\) 的出边),即 \(A\leftarrow A+B,B\leftarrow 0\),答案会增加 \(B(D+v_1-A)\)。
假设翻转所有 \(y\) 的入边及他们子树内的边(不含 \(x\rightsquigarrow y\) 路径上 \(y\) 的入边),即 \(D\leftarrow D+C,C\leftarrow 0\),答案会增加 \(C(A+v_2-D)\)。
其中 \(v_1\ge w_y \ge 1,v_2\ge w_x \ge 1\)。由于此时是最优解,则需满足 \(B(D+v_1-A) \le 0\) 且 \(C(A+v_2-D)\le 0\)。
显然 \(D-A<0\) 和 \(A-D<0\) 不能同时满足,则必然满足 \(B=0\) 或 \(C=0\),即 \(out_x=1\) 或 \(in_y=1\)。
性质 3:若 \(in_x>1\),则考虑所有入边 \((y,x)\),把这条边断开后 \(y\) 所在连通块的所有点均可以到达 \(x\)。(\(out_x\) 同理)
证明:根据 性质 2,所有 \(y\) 的出度均为 \(1\)。归纳可证。
那么首先找到一个 \(deg_x>2\) 的点 \(x\)。若不存在这样的点,说明原图是一条链,显然顺着定向可取得理论最大值(两两可达)。
若 \(in_x\) 和 \(out_x\) 均 \(>1\),根据性质 3,直接得证。
否则不妨设 \(out_x=1\),因为 \(deg_x>2\),所以 \(in_x\) 必然 \(>1\)。只需证明 \(x\) 能到达出边子树里的所有点。
考虑归纳。设 \(x\) 的出边是 \((x,y)\),若 \(deg_y=1\),成立;若 \(deg_y=2\),根据 性质 1,\(y\) 的另一条必然是出边,归纳证明 \((y,y')\)。
否则 \(deg_y>2\)。若 \(in_y=1\),即只有一条 \((x,y)\) 的入边,那么 \(out_y>1\),假设成立;
若 \(in_y\) 和 \(out_y\) 均 \(>1\),仍然直接成立;
否则 \(out_y=1\),还是继续归纳到 \((y,y')\)。
由于图无环,所以归纳可以在有限步内完成,故得证。