2025.2.10 test

A

B

维护序列 \(A\) 支持单点修改，区间查询 \([l,r]\) 中最小的 \(p\) 满足 \(\max_{i\in[l,p]}a_p\le p\)。\(n\le 10^6\)。

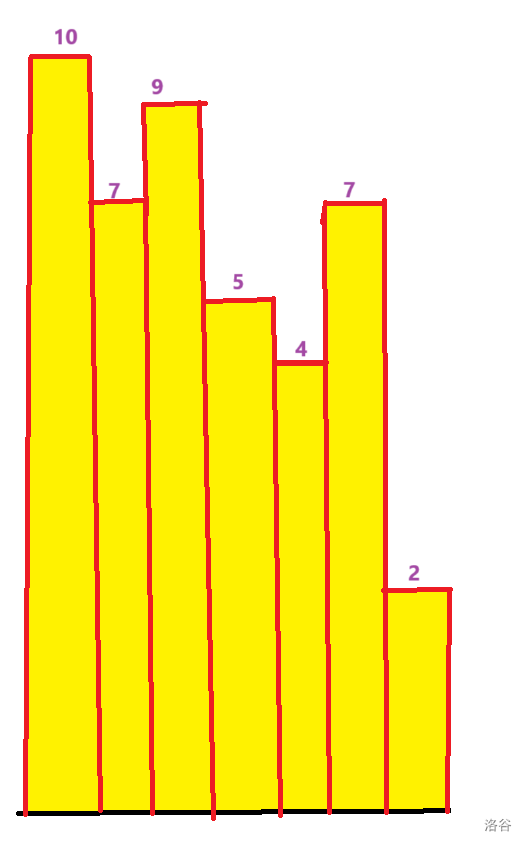
相当于线段树维护单调栈。即我们维护所有满足 \(\max_{i\in[l,p]}\le p\) 中 \(p\) 的最小值。
考虑左右儿子合并，左边会叉掉右边的一些答案，然后这个问题就可以用二分去解决，也就是单侧递归。
具体地，我们只需要求合并两个区间，用左边区间 \(\max\) 去放进右边区间里求右边区间的影响。
只需要判断左边区间 $\max $ 和 \(mid\) 的大小关系，若 \(mid\) 更大那么递归左区间，否则左区间就都被叉了。
我们再讲单 $\log $ 做法，考虑每个节点维护 \(\max_{i\in[l,p]}\le p\) 中 \(p\) 最大值，然后通过线段树二分来求答案。
二分时从 \(l\) 对应的叶子结点往上跳，如果这一步作为左儿子往上跳了，那么就尝试合并该层的右儿子。
如果合并之后区间内存在合法答案，说明答案一定在该右儿子的子树中，此时再在右子树内线段树二分即可。
为什么要维护 \(p\) 的最大值而不是最小值呢？因为我们维护最小值是无法单独维护的，必须要单侧递归实现。
而维护最大值相当于维护了一个区间的可行性，就是说最大的 \(p\) 是最能合法的。

C

给定 \(n\) 对整数 \((x_i,y_i)\)和正整数 \(C\)，求一个定义域和值域都是 \(Z\) 的函数 \(f(x)\)，满足 \(\forall x\in Z\)，\(f(x)+C=f(2f(x)-x+1)\)，使得 \(\sum |f(x_i)-y_i|\) 最小。

考虑从 \(f(x)=w\) 出发可以得到 \(f(2w-x+1)=C+w\)，进一步的继续算，可以得到：
\(f(2C+x)=2C+w,f(2C+2w-x+1)=3C+w\)，则 \(f(x)=f(x-2C)+2C\)，即周期为 \(2C\)。
所以考虑把所有 \((x_i,y_i)\) 都平移到 \(x_i\in[0,2C)\) 处，现在只需要确定 \(f(x)_{0\le x< 2C}\) 的取值即可。
发现 \(f(x)\) 与 \(f(2w-x+1)\) 是挂钩的，相当于他们匹配。我们只需要求他们取值的关系。
令 \(w\in[0,2C)\)，若 \(f(x)=w+2kC\) 那么 \(f(2w-x+1)=w-2kC+C\)。
考虑匹配 \(i,j\)，那么 \(w=(i+j-1)/2\)，可以得出 \(f(i),f(j)\) 的关系，然后就可以算出 \(i,j\) 匹配的代价。
具体地是通过二分找中位数找到最优的 \(f(i),f(j)\)。我们要把所有 \(i,j\in[0,2C)\) 都两两匹配好。
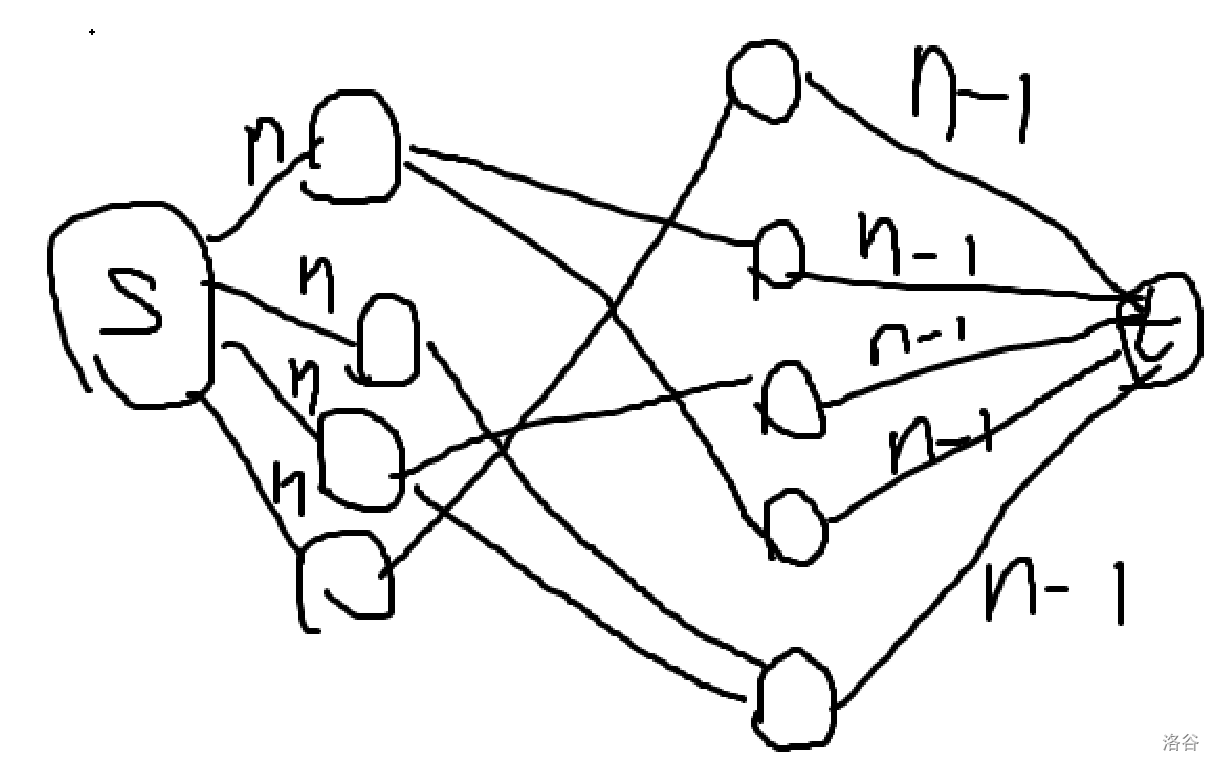
然后由于 \(i,j\) 必定异号所以这就是一个二分图最小权匹配就做完了。