ZR 省选摆烂记

Day 1 - 数据结构

链表

Problem 1 - 洛谷 P10061

很精妙的链表题。

首先考虑特殊性质，旋转整个矩阵改怎么做。

显然只需要维护矩阵旋转了多少次即可。

特殊性质好做的原因正是矩阵的“结构”没有变，原来相邻的数还是相邻，即旋转后的修改可以映射到原来矩阵的修改。

因此考虑用十字链表来维护修改。具体来说，对于每个位置 \((x,y)\)，我们维护周围 4 个位置的 3 个信息：

• 这个位置是在 \((x,y)\) 的上/下/左/右；
• 这个位置的值与 \((x,y)\) 的差；
• 这个位置在未经过任何修改的矩阵中的位置。

并查集

Problem 2 - CF571D

还是比较简单的，应该没有紫。

首先启发式合并，考虑一棵并查集合并组成的树。

我们显然不能在树上下放标记的，所以可以直接打上标记，查询时暴力跳即可。由于启发式合并，跳的层数不会超过 \(O(\log n)\) 层。

因此，我们可以记录上一次子树清零的时间。查询时，在每个节点上二分找出没被清零位置的和，总时间复杂度为 \(O(q\log^2 n)\)。

但实际上，我们发现每个节点的时间标记不交，所以只需要一次二分，可以做到单 \(\log\)。

扫描线

Problem 3 - 洛谷 P9624

首先我们考虑刻画答案。如果移动范围的 X 坐标为 \([-a,b]\)，Y 坐标为 \([-c,d]\)，则答案为 \(a+b+c+d+\min(a,b)+\min(c,d)\)。

首先消去后面的 \(\min\)。枚举 \(a,b\) 之间与 \(c,d\) 之间的四种大小关系。如，当 \(a\le b,c\le d\) 时就有原式等于 \(2a+b+2c+d\)，此时将第三象限内的所有坐标从 \((x,y)\) 变为 \((2x,2y)\) 即可。

接下来就变成了 \(a+b+c+d\) 的 \(\min\)。

考虑对 \(a\) 从大到小扫描线，动态维护对于每个 \(b\) 中的 \(c+d+b\)。

首先令 \(a=\infty\)。此时在二、三象限的点不会对答案有任何影响，因此可以不管。

发现对于 \(x>0\) 的 \((x,y)\)，这个点会对答案产生贡献当且仅当 \(b<x\)，此时 \(c,d\) 就要根据 \(y\) 的正负 \(\operatorname{chkmax}\)。

但是 \(\operatorname{chkmax}\) 不好维护。因为我们都是对前缀 \(\operatorname{chkmax}\) 的，所以 \(c,d\) 的值一定单调不增。

这时候，如果我们要将前缀对 \(T\) 执行 \(\operatorname{chkmax}\)，则我们可以发现，前缀中的一部分不需要修改，剩下的就是区间覆盖。

因此用线段树二分找到第一个需要覆盖的位置，转化为区间覆盖即可。

接下来考虑 \(a\gets a-1\)。不难发现坐标在 \((-a,y)\) 的位置无法覆盖，此时全局 \(\operatorname{chkmax}\) 即可。

Problem 4 - CF983D

差不多懂了，但是还需要看代码理解。

讲解用的代码：https://codeforces.com/contest/983/submission/252374761

线段树合并

Problem 5 - 洛谷 P5298

直接根据 DP 方程算出 \(D_i\)，然后用线段树合并即可。

这里具体讲如何实现线段树合并。

首先，我们发现 DP 方程是一个用左右儿子的前缀和、后缀和组成的式子。然后，我们可以在向下递归的时候分别维护前缀和、后缀和。

Problem 6 - QOJ6322

和上面那题差不多吧。定义 \(f_{x,i}\) 为 \(x\) 为根的连通块中最小值为 \(i\) 的方案数，然后线段树合并即可。

历史和

Problem 7 - CF1824D

首先通过前缀和将下界全部转化成 1，然后扫描线 + 历史和。

接下来可以发现可以用区间求和的线段树解决。

具体实现没怎么听懂，所以写得很简略。

Problem 8 - CF1787I

首先发现一个序列的 beauty 值就是最大可空前缀 + 最大可空子段和。

后面类似 http://cplusoj.com/d/senior/p/665?tid=6737676bfd7bfdc3a346aede，可惜没听懂。。。

分块

Problem 9 - 洛谷 P8360

首先，不能用线段树是因为不能 pushup，不要像我一样差点陷入误区。

然后：

• 对于散块，直接重构。
• 对于整块修改，用带权并查集维护答案。

具体实现等到代码写完会补充一些细节。

Problem 10 - CF1540D

不会，记得补。

长链剖分

Problem 11 - 洛谷 P5291

大概就是先用点减边容斥 + 树形 DP 表达结果，然后长链剖分优化 DP 即可。

Problem 12 - 洛谷 P5411

首先，为了统计答案，我们找到直径中点。如果 \(d\) 为奇数，则中点是一条边；反之中点是一个点。

令 \(f_{x,i}\) 为 \(x\) 子树内离 \(x\) 距离 \(\le i\) 的数量；

\(g_{x,i}\) 为 \(x\) 子树内离 \(x\) 距离 \(\le i\) 到 \(x\) 的距离和；

\(h_{x,i}\) 为 \(x\) 子树内离 \(x\) 距离 \(\le i\) 的点两两之间的距离和；

然后可以推出转移方程。同理可以写出在子树外的转移方程。

接下来用矩阵表示转移，用长链剖分即可。

杂题

Problem 13 - 洛谷 P11369

对操作分块，设块长为 \(B\)。

然后的东西比较难，有空再补。

Problem 14 - CF1693E

不会，记得补。

Problem 15 - CF1740H

性质题。首先发现每个节点的权值是 \(O(\log n)\) 的。具体来说，令 \(f(i)\) 为 \(\operatorname{mex}\) 为 \(i\) 的最小节点数，则 \(f(i)=1+\sum\limits_{j=0}^{i-1} f_j\)。可以归纳证明 \(f(i)=2^i\)。

剩下的有空再补。

Problem 16 - CF1610G

看上去比较简单，但是没听懂。

Problem 17 - CF1464F

不会，记得补。

Problem 18 - 洛谷 P10611

不会，记得补。

Problem 19 - ？

貌似洛谷没有原题。

不过还是不会。

Day 2 - 图论

最短路

Problem 1 - CF1801D

核心：Dijkstra 不一定只能维护最短路。

考虑维护对于每个节点维护 \((x,y)\)，表示当前表演了几次，还剩下 \(y\) 元。

接下来，为了维护消息，我们需要定义 \((x,y)\) 如何比较大小。

显然，如果 \((x1,y1)\)，\((x2,y2)\) 中有 \(x1\le x2,y1\ge y2\)，则有 \((x1,y1)\le(x2,y2)\)。

但是对于其他情况我们不能直接确定大小关系。此时，因为数据范围比较小，所以我们对于每个节点维护一个 \((x,y)\) 的集合，其中任意一个 \((x,y)\) 都表示表演 \(x\) 次，最小花费为 \(y\)。

最小生成树

Problem 2 - AT_cf17_final_j

• Boruvka 算法：每次在连通块中找到一条最小的出边。

首先令当前 \(u\) 点的连通块编号为 \(f_u\)。

接下来我们就要找到 \(u,v\) 使得 \(f_u\not=f_v\)，且 \(w_u+w_v+dis_{u,v}\) 最小。

首先丢弃 \(f_u\not=f_v\) 的限制。不难发现换根 DP 即可。

然后加上 \(f_u\not=f_v\) 的限制。发现我们只需要维护最大、次大（最大和次大的 \(f\) 不相同），就可以保证对于所有 \(u\) 找到 \(v\) 使得 \(u,v\) 满足要求的限制。

欧拉回路

Problem 3 - QOJ 8056

首先发现题目就是在模拟 DFS。所以接下来的就很简单了。

分析一下询问次数：首先每条边会被经过两次，一次往下走一次回溯。

然后每个点还会多向自己的父亲节点询问一次，所以总询问次数肯定是 \(\le 2n+m\) 的。

Problem 4 - QOJ 5434

首先分析答案上限。

定义 \(f(n,i)\) 为长度为 \(n\) 的 01 串中长度为 \(i\) 的子串最多有多少个本质不同的字符串。

不难发现 \(f(n,i)\le\min(2^i,n-i+1)\)，感性理解它是可以取到上界的。

因而可以得出 \(f(n,i)\) 是一个上凸的函数。取 \(f(n,i)\) 的顶点 \(k\)，而显然 \(k\) 为 \(O(\log n)\) 级别的。

也就是说，对于 \(i\le k\) 我们有答案为 \(2^i\)，否则为 \(n-i+1\)。

而显然我们只需要满足 \(f(n,k)\) 和 \(f(n,k+1)\) 都取到上界即可让 \(f(n,1)\sim f(n,n)\) 都取到上界 。

接下来欧拉回路建图即可。

连通性相关

Problem 5 - QOJ 5437

首先边双缩点。显然，对于一个 \(n\) 个点 \(m\) 条边的双连通分量，内部有 \(2^n-m\) 种方法。

但是我不会容斥，所以没怎么听懂。

Problem 6 - 洛谷 P8456

考虑圆方树。

然后不会了。

Problem 7 - 洛谷 P10790

不会，记得补。

Day 2 - 网络流

老师推荐题单：洛谷 training 465429。

最大流

Problem 1 - GYM 102201 J

建图：

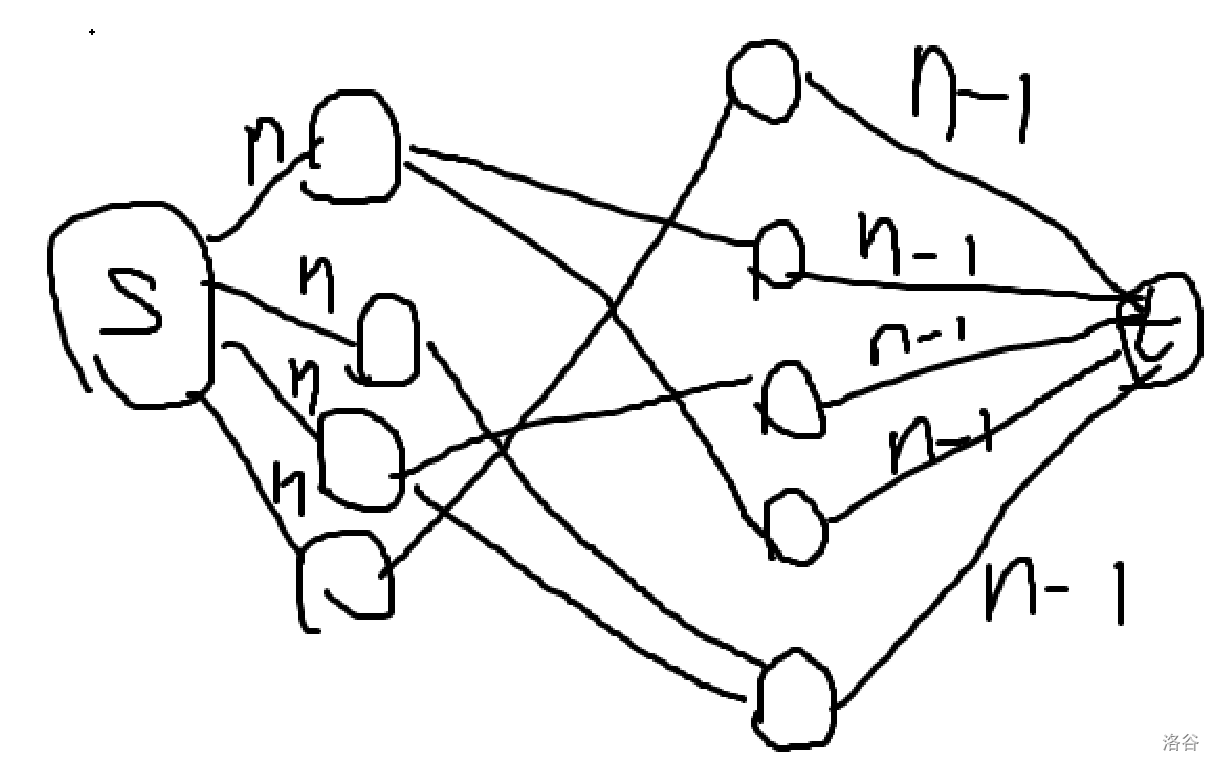
首先，正常跑网络流绝对会超时。

发现左边的的流量均大于右边的流量，且左边的流刚好比右边的流多 1。因此考虑将左边 \(n\) 的流拆成 \(n-1\) 和 \(1\) 的流。

首先处理 \(n-1\) 的流。如果无法全部流到汇点，则无解。

否则一定会剩下一个点到汇点 \(n-1\) 的流和前面 \(n-1\) 个点 \(1\) 的流。此时 BFS 即可。

Problem 2 - 洛谷 P2764

首先答案等于总点数减去最多能合并的点数。

然后考虑怎样才能合并。不难发现，对于一组边 \((u,v)\)，\(u\) 和 \(v\) 能被合并在一条路径时当且仅当 \(u\) 和 \(v\) 都没有被合并过。

接下来就很好做了，不再阐述。

Problem 3 - CF1630F

一个图为二分图等价于没有奇环。

而不难发现，如果有长度为 \(x\) 的环则有长度为 \(x - 1\) 的环。因此这个图为二分图当且仅当没有三元环。因此原条件等价于不存在一个 \(i\) 使得 \(a_i\) 既有因数也有倍数。

接下来拆点。令 \((x,0)\) 表示存在 \(y\) 使得 \(a_x\mid a_y\)，\((x,1)\) 表示存在 \(y\) 使得 \(a_y\mid a_x\)。

考虑连边。对于一组 \(x,y\) 满足 \(a_x\mid a_y\)，我们需要连除了 \((x,1)\) 与 \((y,0)\) 之外的所有 \(x\) 和 \(y\) 之间的边。

接下来的不会了，记得补。

最小割

最大流等于最小割。

更深刻地理解最小割（？）：

• 有 \(n\) 个 01 变量和 \(m\) 个限制 \((x,y,w)\)，表示当 \((x,y)=(0,1)\) 时会产生 \(w\) 的代价；
• \(s\) 恒为 \(0\)，\(t\) 恒为 \(1\)；
• 问最小代价。

上面的问题等价于最小割。

Problem 4 - AGC038F

不会，记得补。

Problem 5 - P4313

由我们前面的部分以及题目的各种细节，不难想到最小割。

因此，我们可以将题目中给出的所有数组加起来，然后减去最小无法取到的值。

对于节点 \(x\) 的 art / science：

• 令 \(s\to x\) 连一条流量为 art 的边，\(x\to t\) 连一条流量为 science 的边；
• 由后面完整的建图，我们必定不会两条边都断掉；
• 断掉 \(s\to x\) 的边表示不选文科，否则代表不选理科。

对于节点 \(x\) 的 same_art / same_science：

• 找到 \(x\) 的四个相邻的位置 \(a,b,c,d\)。
• 由前面的转化，只要 \(x,a,b,c,d\) 中只有一个选了 art，则我们无法获得 same_science 的价值，选 science 同理。
• 但是直接建边肯定会算多遍 same_science。所以我们可以建一个虚点 \(X\)，让 \(x,a,b,c,d\to X\) 连一条 \(\infty\) 的边，让 \(X\to t\) 连一条 same_science 的边。

最后跑最小割即可。

Problem 6 - P3227

会了，不过没写。

Problem 7 - ARC176E

发现 \(X_i,Y_i,A_{i,j}\) 都很小，所以考虑切糕模型。

对于一次操作后，肯定满足 \(\forall j,X_j\ge A_{i,j}\) 或者 \(\forall j,Y_j\ge A_{i,j}\)。

考虑如何处理 \(\forall\)。不难想到，只要有一个不满足条件就连一条 \(+\infty\) 的边即可。

接下来的有空再补。

Hall 定理

这里应该有一个解释，可是我还没补。

Problem 8 - ZROI 某题

不会，记得补。

费用流

Problem 9 - AGC034D

不会，记得补。

模拟费用流

Problem 10 - P1484

不会，记得补。

上下界网络流

Problem 11 - GYM103855I

会了，但是没补。

Day 3 - 组合记数

组合记数

Problem 1 - QOJ9611

因为直接计算式子并不好算，所以考虑原式的组合意义。

定义 \(x\) 为一个长度为 \(n\) 的正整数序列，则原式统计的就是满足 \(x_i\le p_{j,i}\) 的 \(x\) 的个数。

剩下的不会了，记得补。

Problem 2 - QOJ9561

Problem 3 - CF1988F

暴力的想法：直接 DP。

设 \(dp_{n,x,y,z}\) 为长度为 \(n\) 的排列中，\(x\) 个前缀最大值，\(y\) 个后缀最大值，\(z\) 个上升值的方案数。

转移：考虑插入 \(1\)。通过分类讨论可以 \(O(1)\) 转移。总时间复杂度为 \(O(n^4)\)。

考虑优化 DP。

发现前缀最大值出现的位置肯定不会大于最大值的位置，后缀最大值出现的位置肯定不会小于最大值出现的位置，所以我们可以把原 DP 定义中的 \(x,y\) 拆开，分别 DP。

令 \(f_{n,x,z}\) 为长度为 \(n\) 的排列中，\(x\) 个前缀最大值，\(z\) 个上升值的方案数；\(g_{n,y,z}\) 为长度为 \(n\) 的排列中，\(y\) 个后缀最大值，\(z\) 个上升值的方案数。

不难得出 \(f(n)=\sum\limits_{i=1}^n\binom{n-1}{i-1}\sum\limits_{xl}\sum\limits_{yr}\sum\limits_{zl}\sum\limits_{zr} f_{i-1,xl,zl}a_{xl+1}g_{n-i,yr,zr}b_{yr+1}c_{zl+zr+[i\not=n]}\)。

接下来就是简单推式子了，不再叙述。

Problem 4 - CF1086F

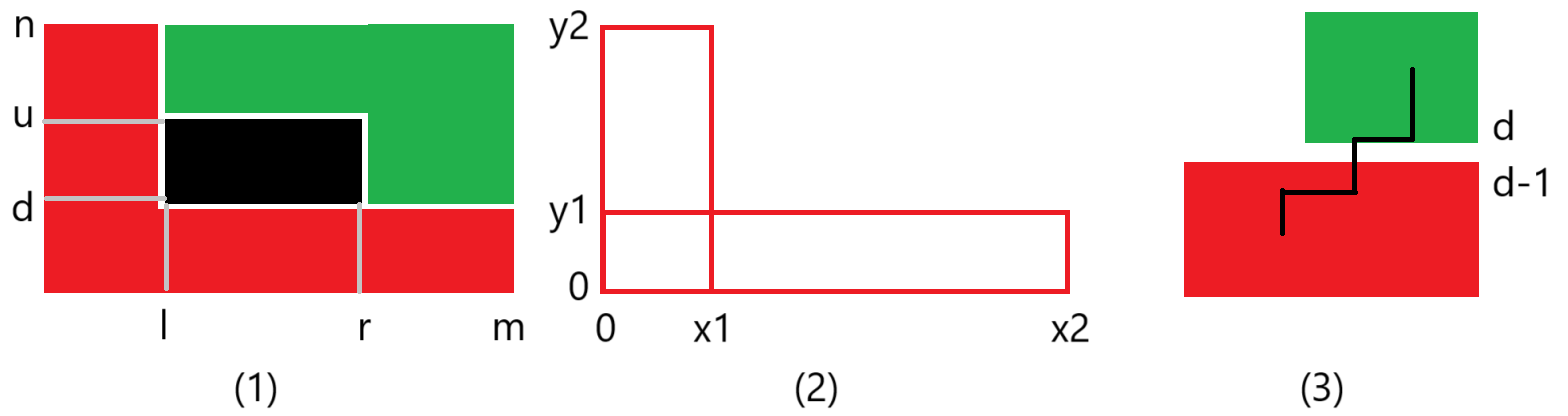
首先答案本身并不好计算，而 \(t\) 时刻着火的数量还是比较好计算的。记 \(f(t)\) 为 \(t\) 时刻着火格子的个数，则答案为 \(f(t)(t+1)-\sum\limits_{i=1}^t f(i)\)。

发现 \(f(i)\) 是矩形面积并，可以考虑容斥。

然后就不会了。。。

Problem 5 - 洛谷 P10360

不会，记得补。

Problem 6 - AGC050F

不会，记得补。

Problem 7 - P9385

不会，记得补。

Problem 8 - CF1349F1

首先发现好序列的个数是 \(n!\) 个，与全排列的数量相同。因此考虑建立全排列与好序列的双射。

通过手玩之后，可以找到一种双射方式。对于一个好序列，将值为 1 的位置倒序加到排列后面，再将值为 2 的位置倒序加到排列后面，以此类推。

接下来考虑计算答案。

由我们的双射方法，可以发现一个好的序列的最大值为 \(x\) 当且仅当恰好有 \(k\) 位置满足 \(a_k<a_{k+1}\)。

剩下的就是简单 DP。令 \(dp_{i,j}\) 为长度为 \(i\) 的序列中满足 \(a_k<a_{k+1}\) 的数量为 \(j\) 的方案数，转移可以考虑加入 1 后的变化。

Problem 9 - jsc2022final_f

link: F - Share the Recipe

不会，记得补。

Day 4 - 数论

素数

• 定义
• 根号级别检测
• 线性筛

Miller-Rabin 素性测试

首先，由费马小定理，有 \(a^{p-1}\equiv 1\pmod p\)。

特判 2。因此 \(p\) 显然为奇数，\(p-1\) 为偶数。

令 \(x\equiv a^{\frac{p-1}{2}}\pmod p\)。由于 \(x^2\equiv1\pmod p\)，所以 \(x\equiv\pm1\pmod p\)。

接下来钦定 \(k\) 个判断的基准数 \(a_1\sim a_k\)，对于每个数 \(a_i\) 都执行下面的操作：

你说得对，但是有空再补。

Pollard-Rho

接下来的有空再补。

逆元

• 定义略。
• 可以证明模 \(p\) 意义下的所有数构成一个域，所以对于任意在 \([0,p)\) 里面的一个整数 \(x\) 都有一个乘法逆元。
• 拓展欧几里得求法。
• 费马小定理求法。

离散对数

• 阶：如果 \((a,p)=1\)，则定义 \(a\) 关于 \(p\) 的阶为最小的 \(x\) 满足 \(a^x\equiv1\pmod p\)，记作 \(\operatorname{ord}_p(a)\)。
• 显然，对于 \(a\) 关于 \(p\) 的阶 \(x\) 满足 \(x\mid\varphi(p)\)。
• 同时，有一个性质：\(\operatorname{ord}_p(a^k)=\dfrac{\operatorname{ord}_p(a)}{(\operatorname{ord}_p(a),k)}\)。
• 证明可以考虑证明 \(\text{LHS}\mid \text{RHS}\) 和 \(\text{RHS}\mid\text{LHS}\)。
• 原根：\(a\) 为 \(p\) 的原根当且仅当 \((a,p)=1\) 且 \(\operatorname{ord}_pa=\varphi(p)\)。
• 离散对数：满足 \(a^x\equiv b\pmod p\) 的 \(x\) 是 \(a\) 关于 \(b\) 在模 \(p\) 意义下的 \(x\)，记作 \(\operatorname{ind}_a(b)\)。做法是 BSGS / exBSGS。

Problem 1 - ？

题面：

给定素数 \(p\) 和序列 \(a,b\)，你需要求出 \(c\)。

其中 \(c_n=\sum\limits_{i\times j\equiv n\pmod p}a_ib_j\)。

做法：

首先，\(i\times j\equiv n\pmod p\Leftrightarrow\log(i)+\log(j)=\log(n)\)。

接下来加法卷积即可。

Problem 2 - 洛谷 P6730

首先考虑建图。如果 \(u,v\) 满足 \(\exists x\) 使得 \((a_u)^x\equiv a_v\pmod p\)，则建一条 \(u\to v\) 的边。

接下来考虑计算答案。首先缩点成一个 DAG。

定义选到的点为黑点，没选到的点为白点。一个点要被选当且仅当这个点是黑点且前面没有白点。接下来就可以用期望的线性法则即可。

考虑暴力建图。同时对两边取个离散对数，可得 \(x\operatorname{ind}_g a_u\equiv\operatorname{ind}_ga_v\pmod p\)，其中 \(g\) 为模 \(p\) 意义下的原根。（由于题目保证 \(p=q^k\land q\in\mathbf{P}\)，所以肯定能找到原根）

由前面阶的性质，\(u\to v\) 有边当且仅当 \(\frac{\operatorname{ord}_p(a_u)}{\operatorname{ord}_p(a_u,k)}=\operatorname{ord}_p(a_v)\)，即 \(\frac{\operatorname{ord}_p(a_u)}{\operatorname{ord}_p(a_v)}=\operatorname{ord}_p(a_u,k)\)。而显然，RHS 可以取到 \(\operatorname{ord}_p(a_u)\) 的任意一个因数，所以 \(u\to v\) 有边的充要条件是 \(\operatorname{ord}_p(a_v)\mid\operatorname{ord}_p(a_u)\)。

至此，本题完成。

中国剩余定理

• CRT：考虑类似拉格朗日插值的做法即可。
• exCRT：简单 exgcd 合并答案。

Problem 3 - 洛谷 P3726

前置知识：范德蒙德卷积，exLucas，一个小定理（？）。

范德蒙德卷积：\(\sum\limits_{i+j=k}\binom{a}{i}\binom{b}{j}=\binom{a+b}{k}\)。

exLucas：略。

一个小定理（？）：对于 \(n\) 为奇数，有 \(\sum\limits_{i=0}^{\frac{n-1}{2}}\binom{n}{i}=\sum\limits_{i=\frac{n+1}{2}}^n=2^{n-1}\)。证明可以用二项式定理。

我们定义，当 \(a<b\) 或者 \(b<0\) 的时候，\(\binom{a}{b}=0\)；。

首先，题目相当于是让我们求 \(\sum\limits_{i=0}^a\sum\limits_{j=0}^{j-1}\binom{a}{i}\binom{b}{j}\)。

将 \(b\) 序列反转（0 变成 1，1 变成 0） 之后，就变成了 \(\sum\limits_{i=0}^a\sum\limits_{i>b-j}\binom{a}{i}\binom{b}{j}\)。

接下来，不难考虑枚举 \(i+j\) 的和。原式变为 \(\sum\limits_{i=b+1}^{a+b}\sum\limits_{j+k=i}\binom{a}{j}\binom{b}{k}\)。

由前面的范德蒙德卷积，我们的式子可以转化为 \(\sum\limits_{i=b+1}^{a+b}\binom{a+b}{i}\)。

接下来考虑计算原式。

首先，我们到现在为止都没有用过 \(b-a\le 10000\) 的条件。

因此考虑用上面的一个小定理。（尽管 \(a+b\) 不一定是奇数，但我们仍然可以用上面定理的一部分，加上对边界条件的特殊处理）

当 \(a+b\) 为偶数时，原式 \(=2^{a+b-1}+\sum\limits_{i=b+1}^{\frac{a+b}{2}}\binom{a+b}{i}\)。

可以证明这个枚举范围 \(\le 5000\)，所以可以过。

Problem 4 - 洛谷 P3301

• 对于 \(\ge a_i\) 的限制：

将将这个数减去 \((a_i-1)\)，然后直接组合数。

• 对于 \(\le a_i\) 的限制：

考虑容斥，然后转化成上面的情况。

Problem 5 - ？

发现每次操作会形成一个置换。于是操作二就是求置换的 \(k\) 次幂。

接下来考虑操作一。发现置换由许多置换环组成。对于每个环，我们都想让它前进 \(a_i\) 步。对于操作次数 \(T\)，需要满足 \(T\equiv a_i\pmod{len_i}\)。接下来 EXCRT 即可。

莫比乌斯反演

• 积性函数：\(\forall (a,b)=1\) 有 \(f(a)f(b)=f(ab)\)。
• 完全积性函数 \(\forall a,b\) 有 \(f(a)f(b)=f(ab)\)。
• 积性函数的性质：只需要定义 \(f(p^k)\)，就确定了 \(f\)，其中 \(p\) 为质数。
• 数论函数的卷积（狄利克雷卷积）：
• \(h=f\circ g\Leftrightarrow h_n=\sum_{d\mid n}f_dg_{\frac{n}{d}}\)。
• 性质：\(h\) 为积性函数。
• 同理可以定义 \(\frac{h}{g}=f\) 当且仅当 \(f\circ g=h\)。求法类似容斥。
• 定义 \(\mu(n)=\begin{cases}1&n=1\\(-1)^k&n=\prod p_i\ \text{且}\ p_i\ \text{两两不同}\\0&\texttt{otherwise}\end{cases}\)。
• 有一个重要性质：\(\sum\limits_{d\mid n}\mu(d)=[n=1]\)。
• 同样可以用 \(\varphi(n)\) 反演。\(\sum\limits_{d\mid n}\varphi(d)=n\)，\(\sum\limits_{d\mid n}d\mu(d)=\varphi(d)\)。
• 莫比乌斯反演：\(f=Id\circ g\Leftrightarrow g=\mu\circ f\)。

Problem 6 - 洛谷 P2257

板子，略过。

Problem 7 - 洛谷 P3455

板子，略过。

Problem 8 - LOJ6076

首先推式子。推出来的结果是 \(\sum\limits_{x}\sum\limits_{y}\sum\limits_{z}\mu(x)\mu(y)\mu(z)\lfloor\frac{a}{\operatorname{lcm}(x,y)}\rfloor\lfloor\frac{b}{\operatorname{lcm}(x,z)}\rfloor\lfloor\frac{c}{\operatorname{lcm}(y,z)}\rfloor\)。

最后发现满足 sigma 里面的式子不为 0 的方案很少，所以直接枚举不为 0 的 \((x,y,z)\) 即可。

Problem 9 - 洛谷 P3327

• 重要性质：\(d(ab)=\sum\limits_{x\mid a}\sum\limits_{y\mid b}[(x,y)=1]\)。

接下来的部分略。

Problem 10 - LOJ6539 / CF1575G

直接推式子即可。需要注意的是由于 \(\mu\circ id=\varphi\)，所以我们还不如用欧拉函数反演。

\[\begin{aligned} 原式&=\sum\limits_{i=1}^n\sum\limits_{j=1}^n\sum\limits_{d|a_i,d|a_j}\varphi(d)\sum\limits_{x|i,x|j}\varphi(x)\\ &=\sum\limits_{d}\sum\limits_{x}\varphi(x)\varphi(d)\sum\limits_{d|a_i,x|i}\sum\limits_{d|a_j,x|j}1\\ &=\sum\limits_{d}\sum\limits_{x}\varphi(x)\varphi(d)f^2(x,d)\\ &\text{其中，}\ f(x,d)=\sum\limits_{d|a_i,x|i}1 \end{aligned} \]

首先，满足 \(f(x,d)\) 不为 \(0\) 的 \((x,d)\) 个数不会超过 \(\sum\limits_{i=1}^nd(a_i)d(i)\)，所以这也是答案的上界。

而根据排序不等式，上面的东西不会超过 \(\sum\limits_{i=1}^nd^2(i)\)。

Problem 11 - 洛谷 P4240

• 首先有 \(\varphi(ab)=\frac{\varphi(a)\varphi(b)\gcd(a,b)}{\varphi(\gcd(a,b))}\)。

首先不难发现必须枚举 \(\gcd\)。

式子记得补。

\[\begin{aligned} \text{ans}&=\sum\limits_{i=1}^n\sum\limits_{j=1}^m\frac{\varphi(i)\varphi(j)\gcd(i,j)}{\varphi(\gcd(i,j))}\\ &=\sum\limits_{i=1}^n\sum\limits_{j=1}^m\varphi(i)\varphi(j)g_{\gcd(i,j)}\qquad (g_i=\frac{i}{\varphi(i)})\\ &=\sum\limits_{i=1}^{\min(n,m)}g_i\sum\limits_{j=1}^n\sum\limits_{k=1}^m[\gcd(j,k)=i]\varphi(j)\varphi(k)\\ &=\sum\limits_{i=1}^{\min(n,m)}g_i\sum\limits_{j=1}^{\lfloor\frac{n}{i}\rfloor}\varphi(ij)\sum\limits_{k=1}^{\lfloor\frac{m}{i}\rfloor}\varphi(ik)\sum\limits_{t|j,t|k}\mu(t)\\ &=\sum\limits_{i=1}^{\min(n,m)}g_i\sum\limits_{t=1}^{\min(n,m)}\mu(t)f(n,i)f(m,i)\qquad (f(i,j)=\sum\limits_{j=1}^{\lfloor\frac{n}{i}\rfloor}\varphi(ij))\end{aligned} \]

筛

• 线性筛略过。
• 杜教筛：求积性函数的前缀和。
• 若 \(f\circ g=h\) 且 \(g\) 和 \(h\) 的前缀和，则我们可以在 \(O(n^{2/3})\) 的时间复杂度内求出 \(f\) 的前缀和 \(f\)。
• 记得补个式子。
• Min_25 筛：
• 首先算出 \(f(x)\) 中 \(x\) 为质数的 \(f\) 的前缀和。
• 然后的不会了，记得补。